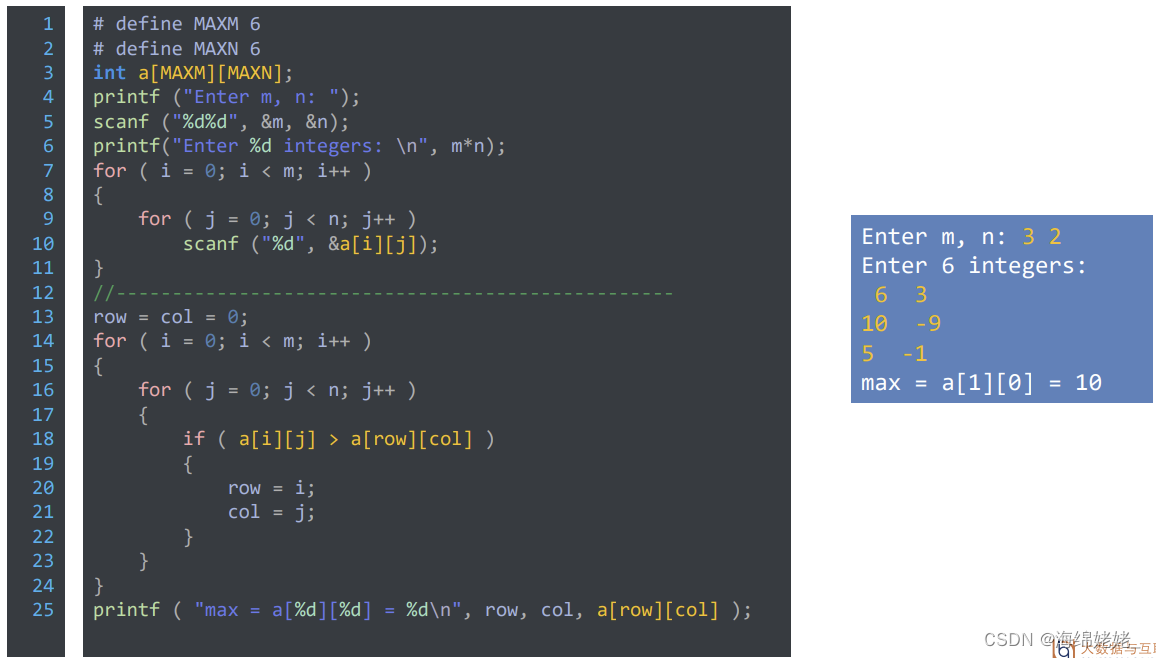
找出矩阵中最大值所在的位置
- 程序解析-求矩阵的最大值

- 源程序段
二维数组
多维数组的空间想象
- 一维数组:一列长表或一个向量
- 二维数组:一个表格或一个平面矩阵
- 三维数组:三位空间的一个方阵
- 多维数组:多维空间的一个数据矩阵

二维数组的定义和引用
- 定义
类型名 数组名[行长度][列长度]
int a[3][2];
定义一个二维数组a,3行2列,6个元素
int b[5][10];
定义一个二维数组b,5行10列,50个元素
引用
先定义,后使用
数组元素的引用:
数组名[行下标][列下标]
行下标和列下标:整形表达式
行下标的取值范围是[0,行长度 - 1]
列下标的取值范围是[0,列长度 - 1]

int a[3][2]; 3行2列,6个元素
a[0][0] a[0][1]
a[1][0] a[1][1]
a[2][0] a[2][1]

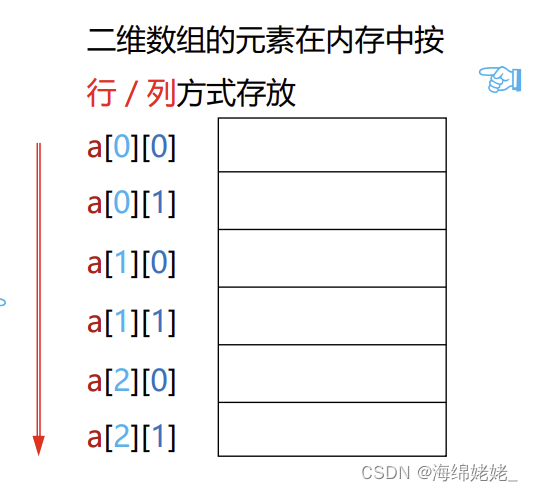
二维数组在内存中的存放方式
int a[3][2];
3行2列,6个元素
表示1个3行2列的矩阵(数表)
a[0][0] a[0][1]
a[1][0] a[1][1]
a[2][0] a[2][1]
二维数组的初始化
- 分行赋初值
int a[3][3] = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
int b[4][3] = {{1, 2, 3}, {}, {4, 5}};

- 顺序赋初值
int a[3][3] = {1, 2, 3, 4, 5, 6, 7, 8, 9}; - 省略行长度
对全部元素都赋了初值
int a[][3] = {1, 2, 3, 4, 5, 6, 7, 8, 9}
或分行赋初值,在初值表中列出了全部行
int b[][3] = {1, 2, 3}, {}, {4, 5}, {}}
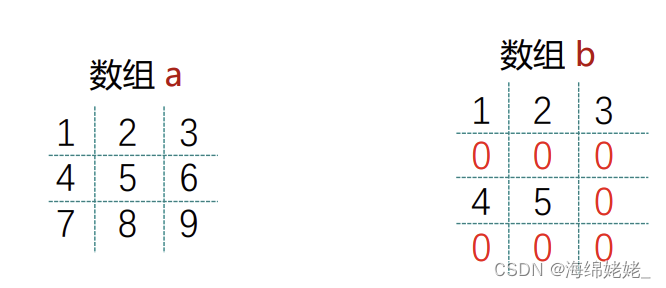
使用二维数组编程
- 行下标和列下标分别作为循环变量,通过二重循环,遍历二维数组
- 通常将行下标i作为外循环的循环变量
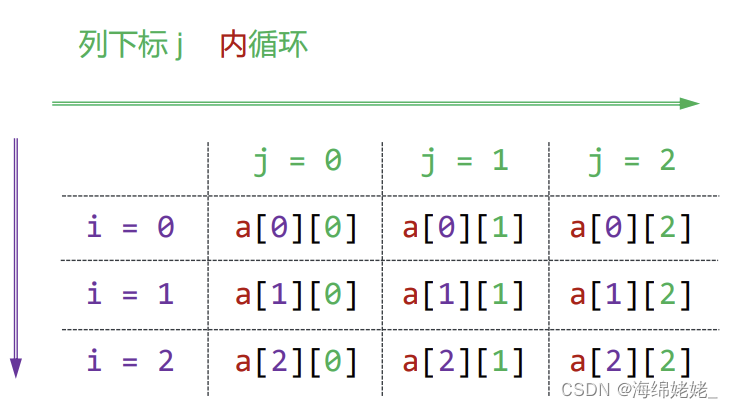
生成一个矩阵(数表)并输出
- 矩阵(数表)的运算通常使用二维数组实现
输入两个正整数m和n(1<= m, n <= 3),生成一个并输出一个m*n的矩阵(数表),其元素的值由下式给出:
a[i][j] = i + j (0 <= i <= m - 1, 0 <= j <= n - 1)
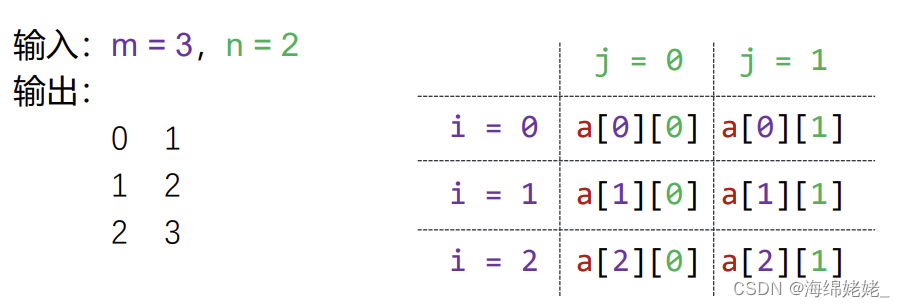
- 源程序
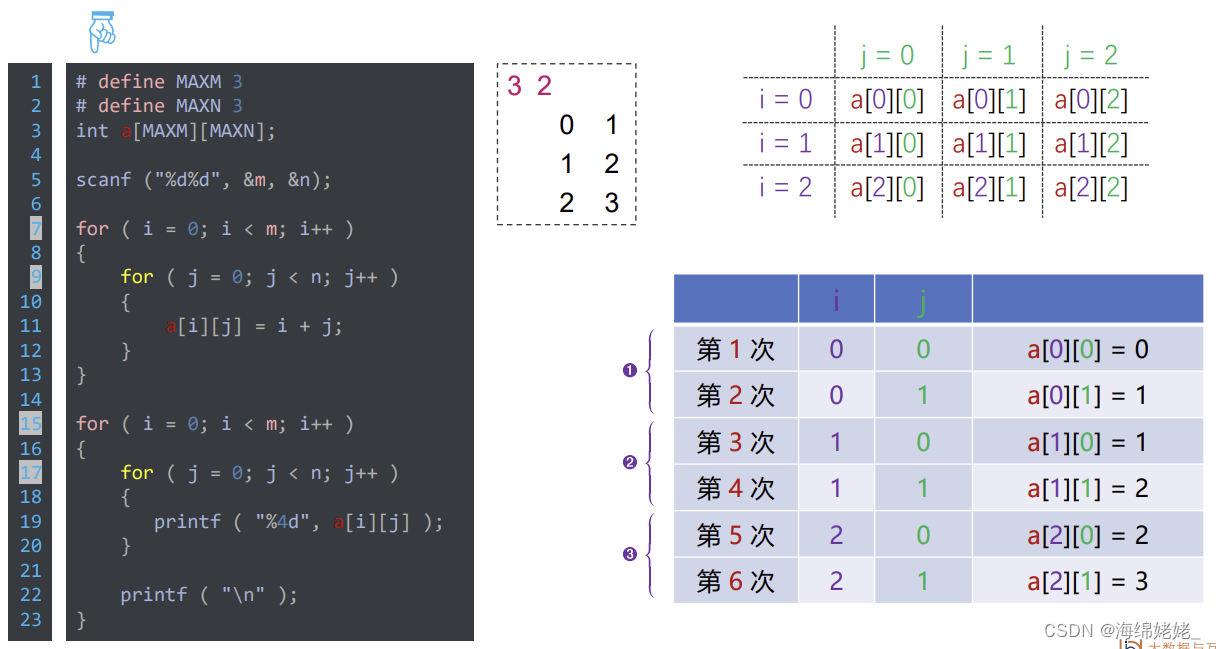
- 矩阵(数表)的输入
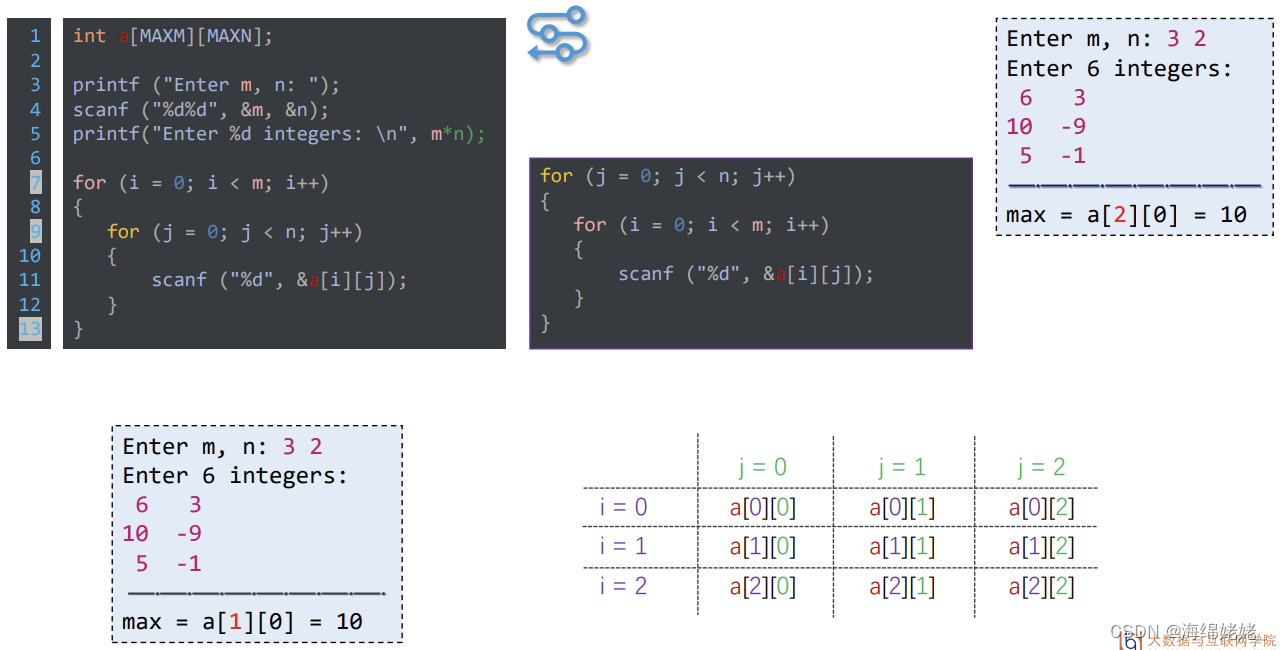
- 矩阵(数表)与二维数组

方阵(方形数表)转置
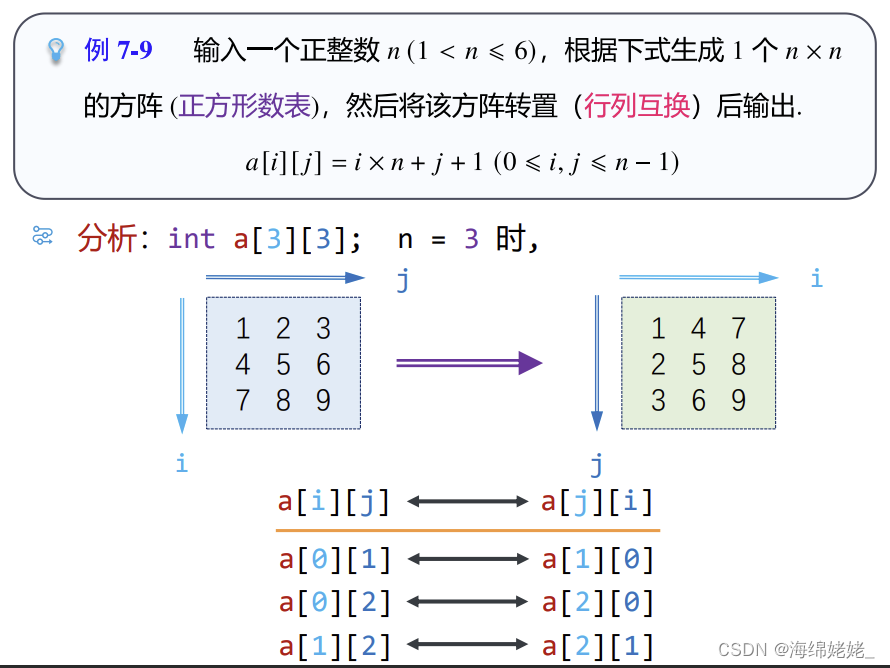
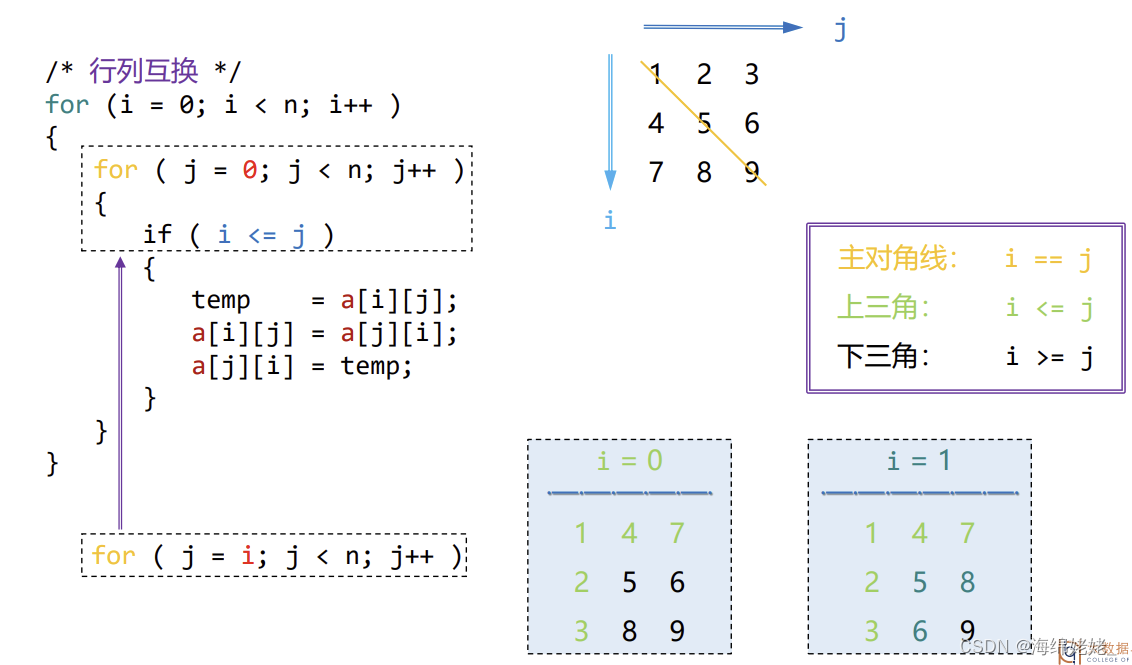
源程序段
计算天数
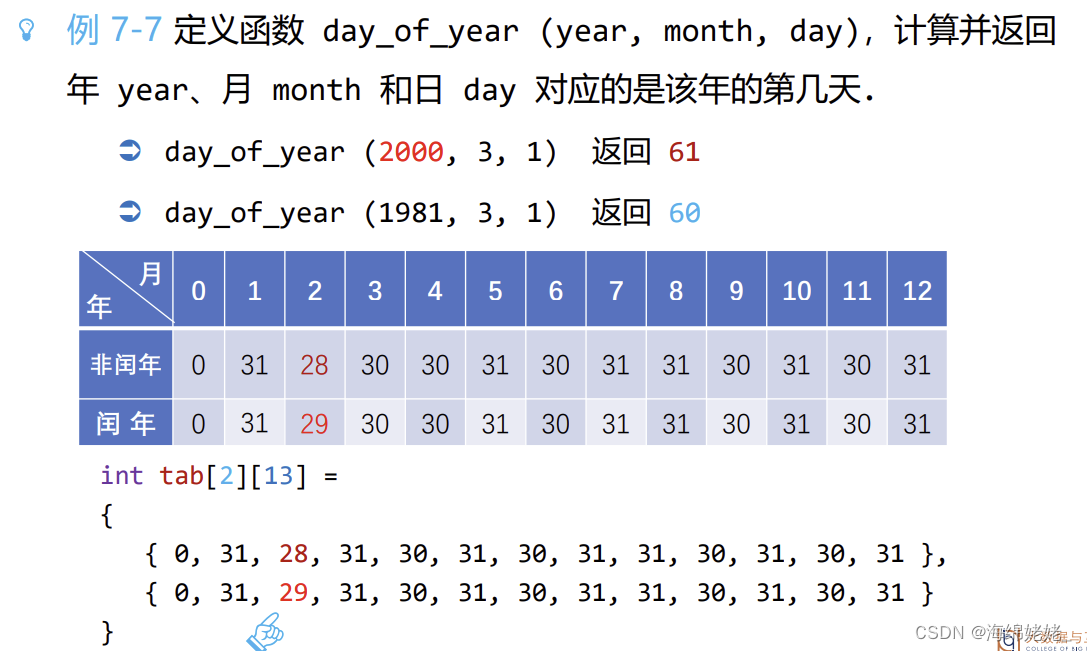
- 函数
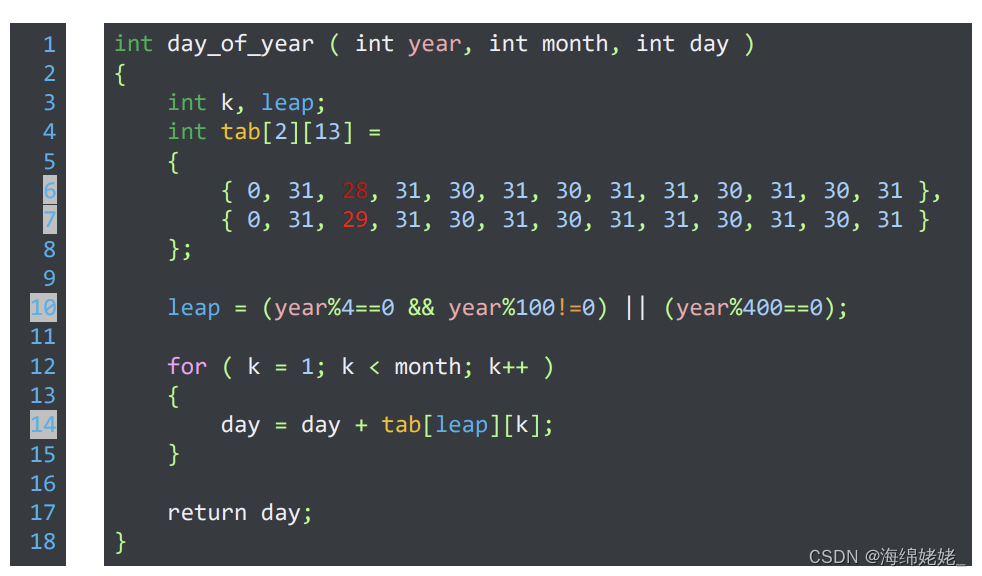
判断回文

- 程序解析
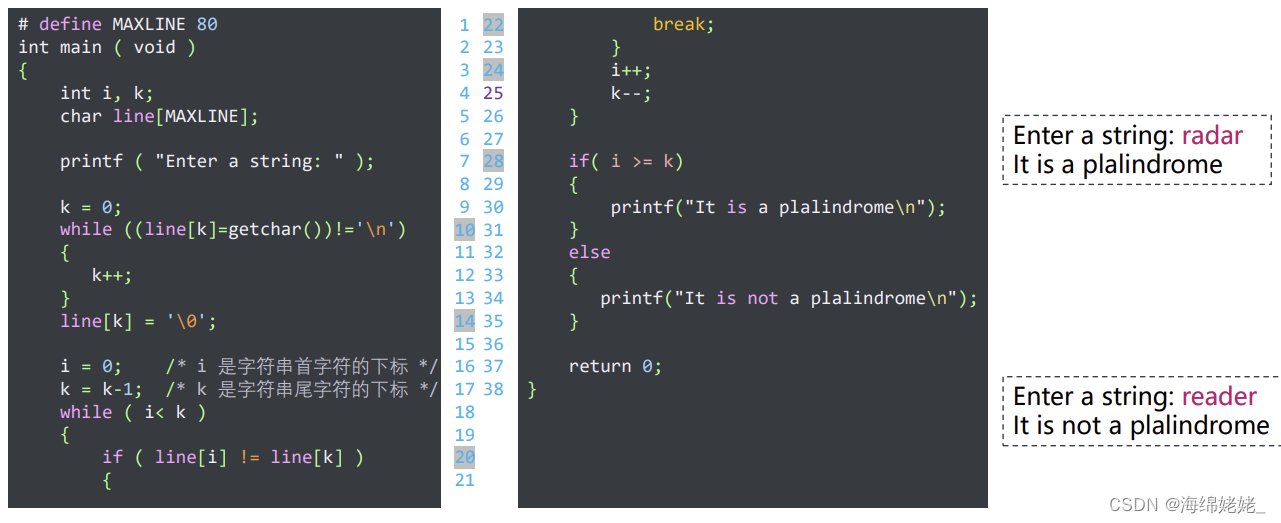
一维字符数组
- 字符串的存储和运算可以用一维数组实现;
- 一维字符数组的定义、引用、初始化与其他类型的一维数组一样;
char str[80];
定义一个含有80个字符型元素的数组str.
char t[5] = {‘H’, ‘a’, ‘p’, ‘p’, ‘y’};

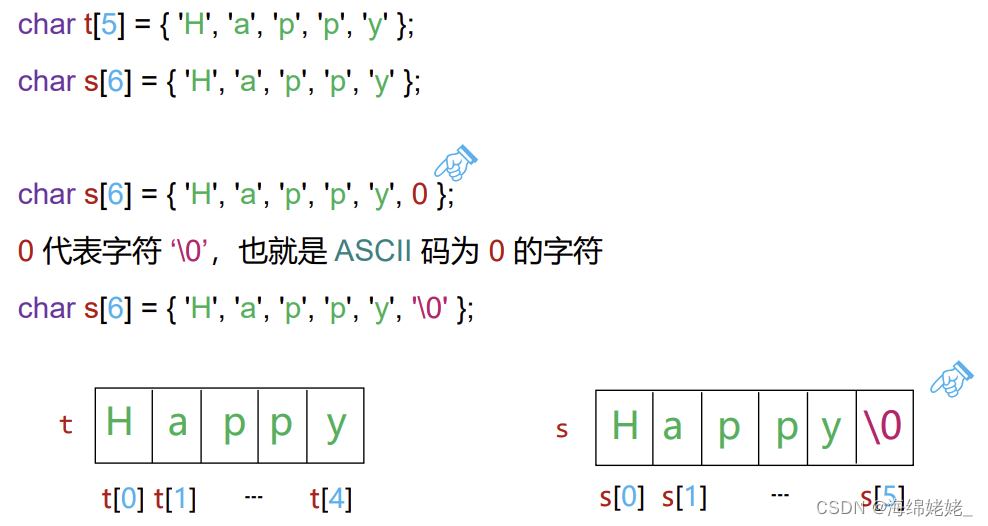
字符串
字符串常量
用一对双括号括起来的字符序列
一个字符串结束符’\n’

字符串与一维字符数组
- 字符串:一个特殊的一维字符数组
- 把字符串放入一维字符数组(存储)
- 对字符串的操作—>对字符数组的操作
字符串的存储–数组初始化
-
字符串可以存放在一维字符数组中
char s[6] = {‘H’, ‘a’, ‘p’, ‘p’, ‘y’, ‘\0’};
字符数组的初始化:用字符串常量
char s[6] = {“Happy”};
char s[6] = “Happy”; -
数组长度>= 字符串的有效长度 + 1
char t[5]; "Happy"能存入t吗?
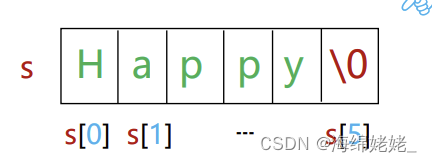
字符串的存储
char s[80] = “Happy”;

- 字符遇‘\0’结束;
- 第一个’\0’前面的所有字符和’\0’一起构成了字符串“Happy";
- '\0’之后的其他数组元素与该字符串无关

对字符串的操作
- 把字符串放入一维字符数组(存储)
- 对字符串的操作---->对字符数组的操作
- 普通字符数组:数组元素的个数是确定的,一般用下标控制循环;
- 字符串:没有显示地给出有效字符的个数,只规定在字符串结束符’\0’之前的字符都是字符串的有效字符,一般用结束符’\0’来控制循环;
循环条件:s[i] != ‘\0’
输出字符串

字符串的存储—赋值和输入
-
把字符串放入一维字符数组(存储)
-
对字符串的操作—>对字符数组的操作
存储
- 数组初始化
char s[6] = “a”; - 赋值
s[0] = ‘a’; s[1] = ‘\0’; - 输入
‘\0’代表空操作,无法输入
输入时,设定一个输入结束符
将输入结束符转换为字符串结束符’\0’
- 数组初始化
使用字符串编程
- C语言将字符串作为一个特殊的一维字符数组来处理
- 存储:把字符串放入一维字符数组
- 数组初始化、赋值、输入
- 存储:把字符串放入一维字符数组
- 对字符串的操作—>对字符数组的操作
- 对一维字符数组的操作:针对字符串的有效字符和字符串结束符
- 检测字符串结束符’\0’
- 对一维字符数组的操作:针对字符串的有效字符和字符串结束符
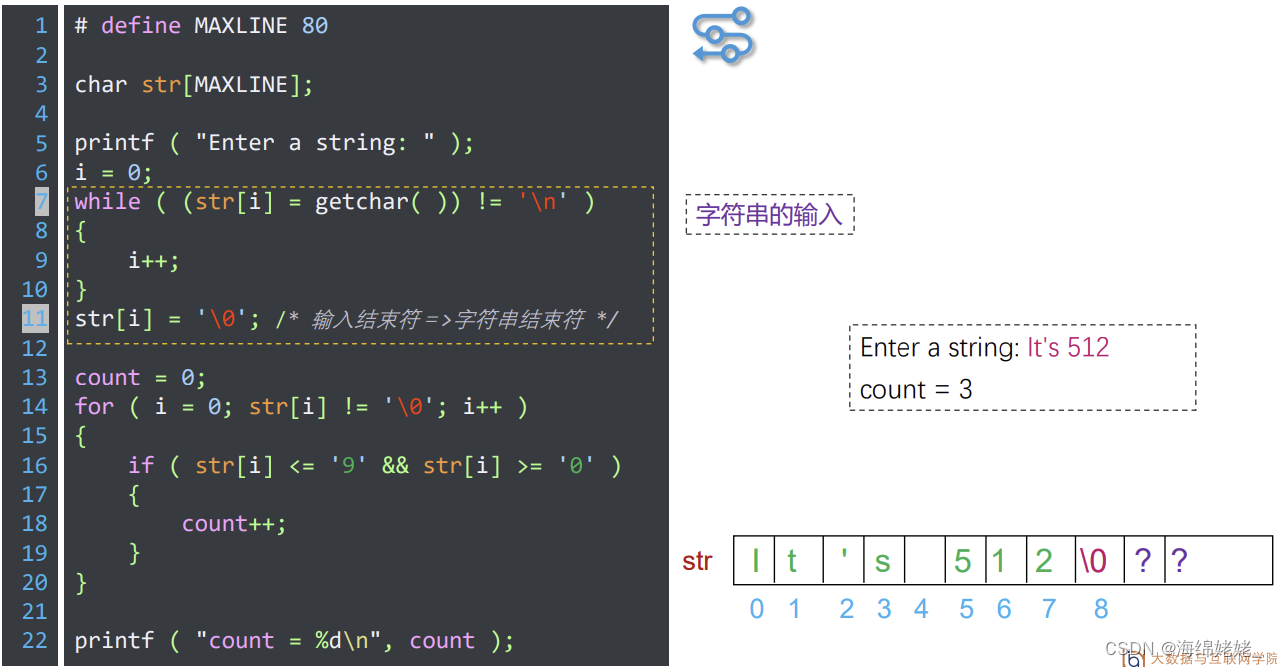
统计数字字符个数

- 源程序段
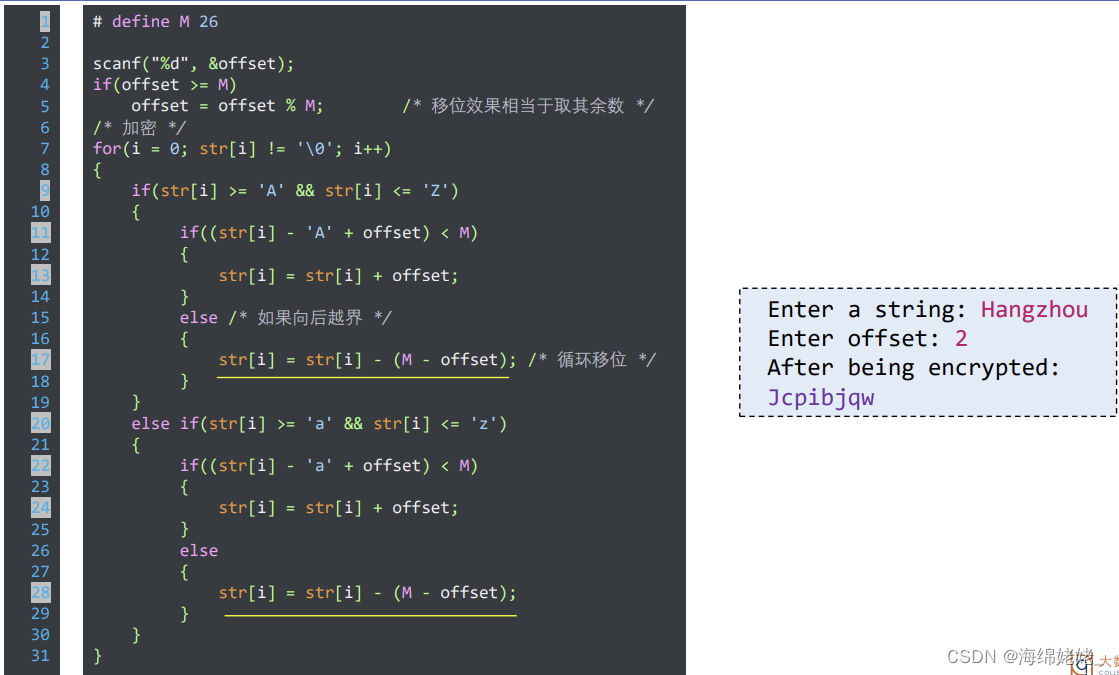
凯撒密码

- 源程序段
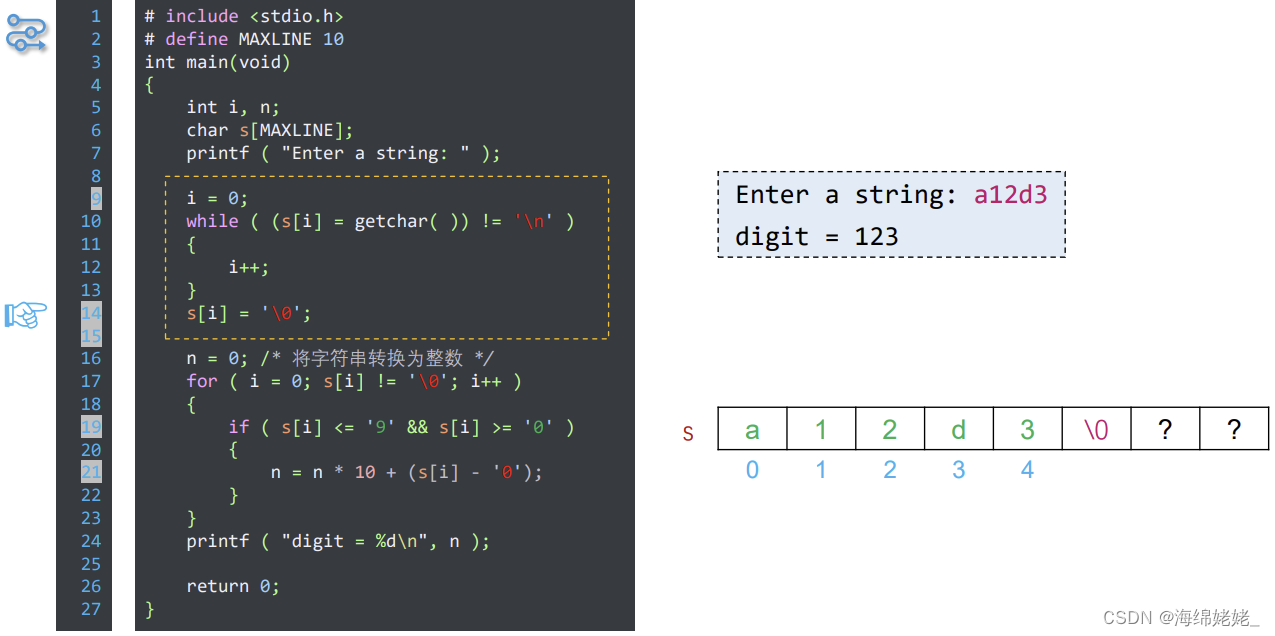
字符转换

- “123”—>123

- 源程序段
- 思考

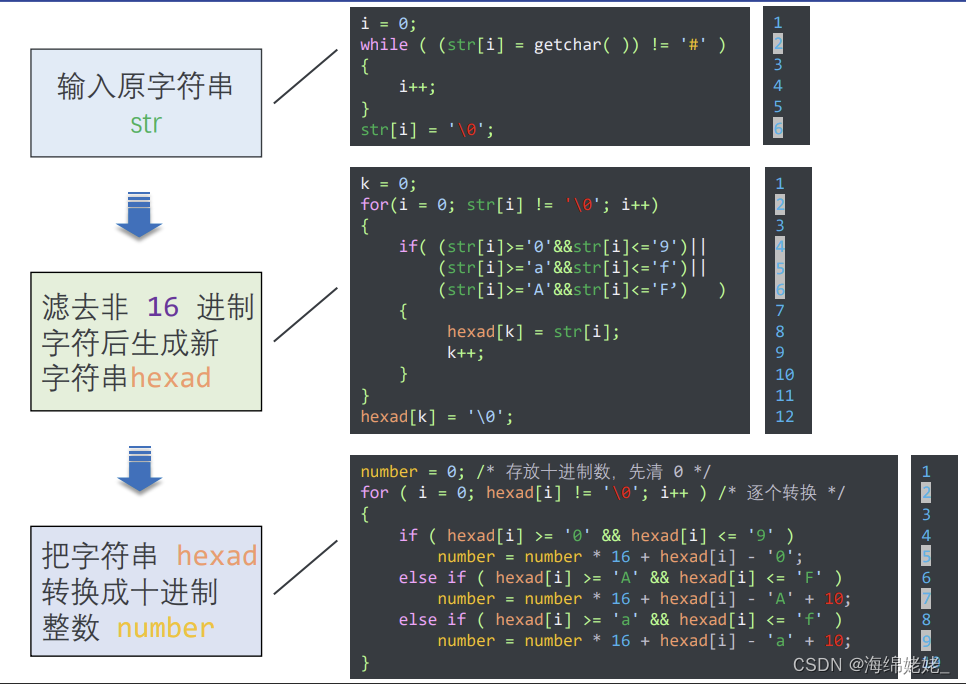
进制转换

- 分析

- 生成十六进制字符串

- 转换为十进制整数
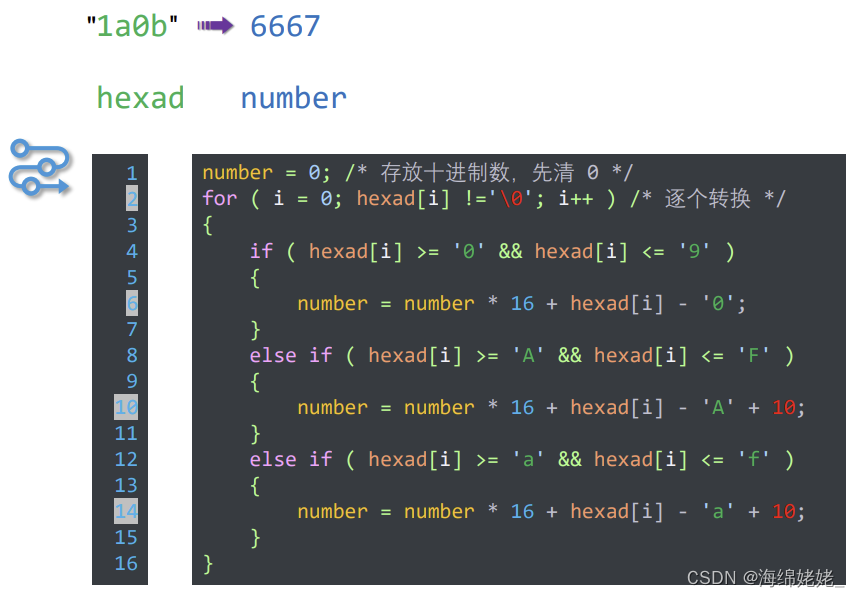
- 程序段
字符串小结
字符串:一个特殊的一维字符数组’\0’
-
把字符串放入一维字符数组(存储)
数组长度足够- 字符数组初始化:char s[80] = “Happy”;
- 赋值:s[0] = ‘a’; s[1] = ‘\0’;
- 输入:输入结束符—>字符串结束符’\0’

-
对字符串的操作—>对字符数组的操作
只针对字符串的有效字符和字符串结束符’\0’

本章总结
- 一维数组:
- 定义、初始化、引用
- 使用一维数组:选择排序、二分查找
- 二维数组
- 定义、初始化、引用
- 使用二维数组:矩阵(数表)
- 字符串
- 字符数组与字符串
- 字符串的存储
- 字符串的操作
- 使用数组进行程序设计