关键词：动态规划 完全背包 记忆化搜索

一个套路：

• 01背包：空间优化之后dp【target+1】，遍历的时候要逆序遍历
• 完全背包：空间优化之后dp【target+1】，遍历的时候要正序遍历

题目：

方法一：

动态规划 完全背包

思路：

就是一个完全背包问题。有无限个相同的硬币。目标就是amount。

状态：dp[j]判断在放第i种硬币时，凑成目标金额为j所需要的最少硬币个数。（进行了滚动数组进行空间优化，正序遍历）

转移方程： dp[j]=min(dp[j],dp[j-coins[i]]+1)

• 如果选dp[j]：不加这个硬币。
• 如果选dp[j-coins[i]]+1：加这一个硬币。

初始条件：因为是找最小值，所以dp初始值设置成一个比较大的值，我设了1e5。

边界条件：初始条件里面，dp[0]要特别设置出来，dp[0]=0。因为在目标为0元、什么硬币都不用的时候，所需要的最少硬币个数为0。

画了一个dp状态推理过程的表格。纵坐标是j，横坐标是i。实际上dp状态是一维的，长度为amount+1，coins维被空间优化了。

amount\coins	0	1	2	5
0	0
1	10000	1
2	10000	2	1
3	10000	3	2
4	10000	4	2
5	10000	5	3	1
6	10000	6	3	2
7	10000	7	4	2
8	10000	8	4	3
9	10000	9	5	3
10	10000	10	5	2
11	10000	11	6	3

 复杂度计算：

• 时间复杂度O(nm) n为amount m为coins.size()
• 空间复杂度O(n) n为amount

代码：

#include <vector>
#include <iostream>
class Solution {
public:int coinChange(std::vector<int>& coins, int amount) {if (amount == 0) return 0;std::vector<int> dp(amount + 1,1e5);dp[0] = 0;for (int i = 0; i < coins.size(); ++i){for (int j = coins[i]; j <= amount; ++j){dp[j] = std::min(dp[j], dp[j - coins[i]] + 1);}}if (dp[amount] == 1e5) return -1;else return dp[amount];}
};

方法二：

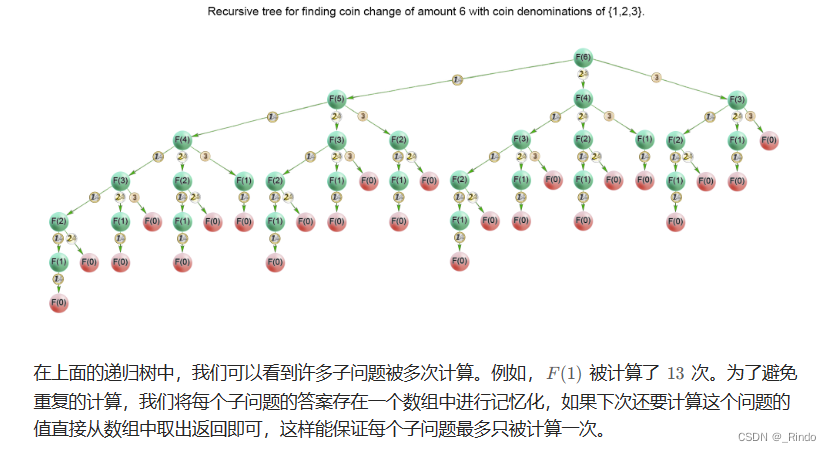
动态规划 记忆化

思路：

记忆化：把之前算过的状态记下来，减少搜索。

 复杂度计算：

• 时间复杂度O(nm) n为amount m为coins.size()
• 空间复杂度O(n) n为amount

 代码：

class Solution {std::vector<int>count;int dp(std::vector<int>& coins, int rem){if (rem < 0)return-1;if (rem == 0)return 0;if (count[rem - 1] != 0)return count[rem - 1];int min = INT_MAX;for (const auto& coin : coins){int res = dp(coins, rem - coin);if (res >= 0 && res < min){min = res + 1;//为什么要加个1}}count[rem - 1] = min == INT_MAX ? -1 : min;return count[rem - 1];}
public:int coinChange(std::vector<int>& coins, int amount) {if (amount < 1) return 0;count.resize(amount);return dp(coins, amount);}
};

题目二：

给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。

思路：

和上面唯一不同的是求的是凑成总金额的硬币组合数。

其实是基本一样的思路，主要是改变转移方程。

状态：dp[j]判断在放第i种硬币时，凑成目标金额为j的硬币组合数。（进行了滚动数组进行空间优化，正序遍历）

转移方程： dp[j]=dp[j]+dp[j-coins[i]]

• dp[j]：不加这个硬币，凑成j的组合数。
• dp[j-coins[i]]：加这一个硬币，凑成j的组合数。

初始条件：因为是找总和，所以dp初始值设置成0。

边界条件：初始条件里面，dp[0]要特别设置出来，dp[0]=1。因为在凑0元的时候，有一个方法就是啥都不放。

画了一个dp状态推理过程的表格。纵坐标是j，横坐标是i。实际上dp状态是一维的，长度为amount+1，coins维被空间优化了。

amount\coins	0	1	2	5
0	1
1	0	1
2	0	1	2
3	0	1	2
4	0	1	3
5	0	1	3	4
6	0	1	4	5
7	0	1	4	6
8	0	1	5	7
9	0	1	5	8
10	0	1	6	10
11	0	1	6	11

 复杂度计算：

• 时间复杂度O(nm) n为amount m为coins.size()
• 空间复杂度O(n) n为amount

代码：

#include <vector>
#include <iostream>
//和前面问题不一样：
//给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
class Solution {
public:int coinChange(std::vector<int>& coins, int amount) {if (amount == 0) return 0;std::vector<int> dp(amount + 1, 0);dp[0] = 1;for (int i = 0; i < coins.size(); ++i){for (int j = coins[i]; j <= amount; ++j){dp[j] += dp[j - coins[i]];}}return dp[amount];}
};