数据结构：第7章：查找(复习）

顺序查找：

折半查找：

二叉排序树：

4. (程序题)

平衡二叉树：

顺序查找：

ASL= $\frac{1}{n}\sum i=\frac{1+n}{2}$

折半查找：

$ASL=\frac{1}{n}\sum_{i=1}^{h}j*2^{j-1}$ $=\frac{n+1}{n}log2(n+1)-1$

这里 j 表示二叉查找树的第 j 层

二叉排序树：

二叉排序树（Binary Search Tree，BST）是一种特殊的二叉树，定义：

对于二叉排序树的每个节点，其左子树的所有节点的值都小于该节点的值。
对于二叉排序树的每个节点，其右子树的所有节点的值都大于该节点的值。
对于二叉排序树的每个节点，其左右子树也分别是二叉排序树。

可以发现二叉排序树的定义时递归定义。

这些性质保证了对于二叉排序树中的任意节点，其左子树的节点值小于它，右子树的节点值大于它，从而形成了一种有序的结构。

二叉排序树的有序性质使得在其中进行查找、插入和删除等操作时具有较高的效率。对于给定的值，可以通过比较节点的值，按照二叉排序树的性质在树中快速定位所需的节点。

二叉排序树的难点在于删除树中的某个值。删除某个键值为 key 的节点时，有三中情况要考虑：

1.该节点 r 的左孩子为空：r=r->lch;

2.该节点 r 的右孩子为空：l=l->rch;

3.该节点的左右孩子均不位空：选择左孩子中 key 值最大的节点替换 r；

4. (程序题)

二叉排序树插入、删除

键盘输入若干整型数据，以0做结束，利用二叉排序树的插入算法创建二叉排序树，并中序遍历该二叉树。之后输入一个整数x，在二叉排序树中查找，若找到则输出“该数存在”，否则输出“该数不存在”；再输入一个要删除的一定存在的整数y，完成在该二叉树中删除y的操作，并输出删除y后的二叉树中序遍历的结果。

输出数据之间用一个空格分隔。

输入：
1 5 4 2 3 6 8 7 9 11 14 13 12 16 19 0
输出：
1 2 3 4 5 6 7 8 9 11 12 13 14 16 19
输入：
19
输出：
该数存在
输入：
14
输出：
1 2 3 4 5 6 7 8 9 11 12 13 16 19

#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
using namespace std;
typedef long long LL;typedef struct Info {int key;
}Info;typedef struct Node {Info data;struct Node* lch;struct Node* rch;
}Node,*Tree;void print(Tree& r) {if (r == NULL)return;print(r->lch);cout << r->data.key << " ";print(r->rch);
}void Insert(Tree& r, int key) {if (r == NULL) {Node* p = new Node;p->data.key = key;p->rch = p->lch = NULL;r = p;}else if(r->data.key<key) {Insert(r->rch, key);}else {Insert(r->lch, key);}
}void build(Tree& r) {int in;cin >> in;while (in) {Insert(r, in);cin >> in;}
}int search(Tree& r, int key) {if (r == NULL)return 0;if (r->data.key == key) {return 1;}if (r->data.key < key) {if (search(r->rch, key))return 1;}else {if (search(r->lch, key))return 1;}return 0;
}int del(Tree& r, int key) {if (r == NULL)return 0;if (r->data.key == key) {if (r->lch == NULL) {r =r->rch;}else if (r->rch == NULL) {r =r->lch;}else {//cout << r->data.key << endl;Node* p = r->lch;Node* fa = r;while (p->rch != NULL) {fa = p;p = p->rch;}Node* t = r;if (fa != r)fa->rch = p->lch;if (r->lch != p)p->lch = r->lch;p->rch = r->rch;//cout << p->data.key << endl;r = p;delete t;}return 1;}if (r->data.key < key) {if (del(r->rch, key))return 1;}else {if (del(r->lch, key))return 1;}return 0;
}int main() {Node* root = NULL;build(root);print(root);int in;cin >> in;if (search(root, in)) {cout << "该数存在" << endl;}else {cout << "该数不存在" << endl;}cin >> in;del(root, in);print(root);return 0;
}

用例1：

输入

1 5 4 2 3 6 8 7 9 11 14 13 12 16 19 0 19 14

输出

1 2 3 4 5 6 7 8 9 11 12 13 14 16 19 该数存在 1 2 3 4 5 6 7 8 9 11 12 13 16 19

用例2：

输入

10 9 8 7 11 12 13 14 0 14 8

输出

7 8 9 10 11 12 13 14 该数存在 7 9 10 11 12 13 14

用例3：

输入

23 45 67 21 12 15 9 10 55 0 19 9

输出

9 10 12 15 21 23 45 55 67 该数不存在 10 12 15 21 23 45 55 67

平衡二叉树：

平衡二叉树的定义

平衡二叉排序树查找算法的性能取决于二叉树的结构,而二叉树的形状则取决于其数据集。
如果数据呈有序排列,则二叉排序树是线性的,查找的时间复杂度为O(n);反之,如果二叉排序
树的结构合理,则查找速度较快,查找的时间复杂度为O(logn)。事实上,树的高度越小,查找
速度越快。因此,希望二叉树的高度尽可能小。本节将讨论一种特殊类型的二叉排序树,称为平
衡二叉树(Balanced Binary Tree 或 Height-Balanced Tree),因由前苏联数学家 Adelson-Velskii 和
Landis 提出,所以又称AVL树。

平衡二叉树或者是空树,或者是具有如下特征的二叉排序树:
(1)左子树和右子树的深度之差的绝对值不超过1;
(2)左子树和右子树也是平衡二叉树。

若将二叉树上结点的平衡因子(Balance Factor,BF)定义为该结点左子树和右子树的深度之
差,则平衡二叉树上所有结点的平衡因子只可能是-1、0和1。只要二叉树上有一个结点的平衡
因子的绝对值大于1,则该二叉树就是不平衡的。图7.11(a)所示为两棵平衡二叉树,而图 7.11
(b)所示为两棵不平衡的二叉树,结点中的值为该结点的平衡因子。

平衡二叉树的调整（重难点）

LL型调整操作：由于在A左子树根结点的左子树上插入结点，A的平衡因子由1增至2，致使以A为根的子树失去平衡，则需进行一次向右的顺时针旋转操作

RR 型调整操作：当在 A 的右子树的右子树上插入结点时，A 的平衡因子由 -1 变为 -2，导致以 A 为根结点的子树失去平衡。此时，需要进行一次向左的逆时针旋转操作，将 A 的右子树作为其左子树的右子树，并将 A 作为其左子树的根结点。

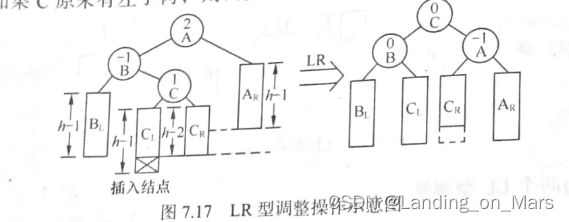
LR型调整操作：由于在A的左子树根结点的右子树上插入结点, A的平衡因子由1增至2,致使以A为根结点的子树失去平衡，则需进行两次旋转操作。第一次对B及其右子树进行递时针旋转,C转上去成为B的根，这时变成了LL型，所以第二次进行LL型的顺时针旋转即可恢复平衡。如果C原来有左子树，则调整C的左子树为B的右子树，

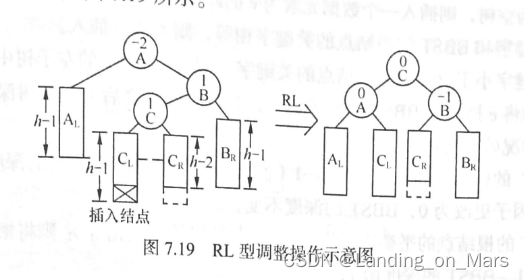
RL型调整操作：由于在A的右子树根结点的左子树上插入结点，A的平衡因子由-1变为-2，致使以A 为根结点的子树失去平衡，则旋转方法和LR型相对称，也需进行两次旋转，先顺时针右旋，再逆时针左旋。

左，右旋转调整代码：

 void Turnleft(TreeNode*& r) {TreeNode* A = r;TreeNode* B = r->right;A->right = B->left;B->left = A;r = B;}void Turnright(TreeNode*& r) {TreeNode* A = r;TreeNode* B = r->left;A->left = B->right;B->right = A;r = B;}

判断不平衡类型类型的代码：

void fun1(vector<int>& g, TreeNode* r) {if ( r == NULL||(r->left==NULL&&r->right==NULL))return;if (mp[r->left] == mp[r->right])return;g.push_back(mp[r->left] - mp[r->right]);fun1(g, r->left);fun1(g, r->right);}string check(TreeNode* root) {vector<int>g;fun1(g, root);if (g[0] == 2&&g[1]==1)return "LL";else if (g[0] == 2&&g[1]==-1)return "LR";else {if (g[0] == -2&&g[1]==1)return "RL";return "RR";}return "NO";}

将二叉树转换成平衡二叉树的代码：


class Solution {
public:unordered_map<TreeNode*, int>mp;void fun1(vector<int>& g, TreeNode* r) {if ( r == NULL||(r->left==NULL&&r->right==NULL))return;if (mp[r->left] == mp[r->right])return;g.push_back(mp[r->left] - mp[r->right]);fun1(g, r->left);fun1(g, r->right);}string check(TreeNode* root) {vector<int>g;fun1(g, root);if (g[0] == 2&&g[1]==1)return "LL";else if (g[0] == 2&&g[1]==-1)return "LR";else {if (g[0] == -2&&g[1]==1)return "RL";return "RR";}return "NO";}void Turnleft(TreeNode*& r) {TreeNode* A = r;TreeNode* B = r->right;A->right = B->left;B->left = A;r = B;}void Turnright(TreeNode*& r) {TreeNode* A = r;TreeNode* B = r->left;A->left = B->right;B->right = A;r = B;}void change(TreeNode*& r, string ret) {if (ret == "LL") {Turnright(r);mp[r] = mp[r->left] + 1;}else if (ret == "RR") {Turnleft(r);mp[r] = mp[r->left] + 1;}else if (ret == "RL") {Turnright(r->right);Turnleft(r);mp[r] = mp[r->left] + 1;}else {Turnleft(r->left);Turnright(r);mp[r] = mp[r->left] + 1;}}int dfs(TreeNode*& root) {if (root == NULL) {return 0;}int lh = dfs(root->left);int rh = dfs(root->right);int h = lh - rh;//cout << "__________________" << lh << " " << rh << " " << h << "______"<<root->val<<endl;if (h == 2 || h == -2) {//cout << root->val << endl;string ret = check(root);//cout << ret << endl;change(root, ret);}mp[root] = max(lh, rh) + 1;return max(lh,rh)+1;}TreeNode* balanceBST(TreeNode* root) {dfs(root);return root;}
};

完整代码：

代码中有测试样例

#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
using namespace std;// Definition for a binary tree node.
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};// Function to insert a value into BST
TreeNode* insertIntoBST(TreeNode* root, int val) {if (!root) {return new TreeNode(val);}if (val < root->val) {root->left = insertIntoBST(root->left, val);}else {root->right = insertIntoBST(root->right, val);}return root;
}// Function to construct BST from preorder traversal
TreeNode* bstFromPreorder(vector<int>& preorder) {TreeNode* root = nullptr;for (int val : preorder) {if (val == 0)continue;root = insertIntoBST(root, val);}return root;
}// Function to perform inorder traversal (for verification)
void inorderTraversal(TreeNode* root) {if (root) {inorderTraversal(root->left);cout << root->val << " ";inorderTraversal(root->right);}
}// Function to perform level order traversal
void levelOrderTraversal(TreeNode* root) {if (!root) {return;}queue<TreeNode*> q;q.push(root);while (!q.empty()) {TreeNode* current = q.front();q.pop();cout << current->val << " ";if (current->left) {q.push(current->left);}if (current->right) {q.push(current->right);}}
}class Solution {
public:unordered_map<TreeNode*, int>mp;void fun1(vector<int>& g, TreeNode* r) {if ( r == NULL||(r->left==NULL&&r->right==NULL))return;if (mp[r->left] == mp[r->right])return;g.push_back(mp[r->left] - mp[r->right]);fun1(g, r->left);fun1(g, r->right);}string check(TreeNode* root) {vector<int>g;fun1(g, root);if (g[0] == 2&&g[1]==1)return "LL";else if (g[0] == 2&&g[1]==-1)return "LR";else {if (g[0] == -2&&g[1]==1)return "RL";return "RR";}return "NO";}void Turnleft(TreeNode*& r) {TreeNode* A = r;TreeNode* B = r->right;A->right = B->left;B->left = A;r = B;}void Turnright(TreeNode*& r) {TreeNode* A = r;TreeNode* B = r->left;A->left = B->right;B->right = A;r = B;}void change(TreeNode*& r, string ret) {if (ret == "LL") {Turnright(r);mp[r] = mp[r->left] + 1;}else if (ret == "RR") {Turnleft(r);mp[r] = mp[r->left] + 1;}else if (ret == "RL") {Turnright(r->right);Turnleft(r);mp[r] = mp[r->left] + 1;}else {Turnleft(r->left);Turnright(r);mp[r] = mp[r->left] + 1;}}int dfs(TreeNode*& root) {if (root == NULL) {return 0;}int lh = dfs(root->left);int rh = dfs(root->right);int h = lh - rh;//cout << "__________________" << lh << " " << rh << " " << h << "______"<<root->val<<endl;if (h == 2 || h == -2) {//cout << root->val << endl;string ret = check(root);//cout << ret << endl;change(root, ret);}mp[root] = max(lh, rh) + 1;return max(lh,rh)+1;}TreeNode* balanceBST(TreeNode* root) {dfs(root);return root;}
};int main() {vector<int> preorder={ 31,25,47,16,28,0,0,0,0,0,30,0,0 };/*31,25,47,0,0,40,69,0,43,0,0 ,0,0            RL1,0,2,0,3,0,4,0,0                         RR31,25,47,0,0,40,69,36,0,0,0 ,0,0            RL31,25,47,16,28,0,0,0,0,26,0,0,0             LR31,25,47,16,28,0,0,0,0,0,30,0,0             LR*/TreeNode* root = bstFromPreorder(preorder);// Verification by performing inorder traversalinorderTraversal(root);cout << endl;levelOrderTraversal(root);cout << endl;Solution solve;root=solve.balanceBST(root);levelOrderTraversal(root);cout << endl;return 0;
}