【数据结构】七、图

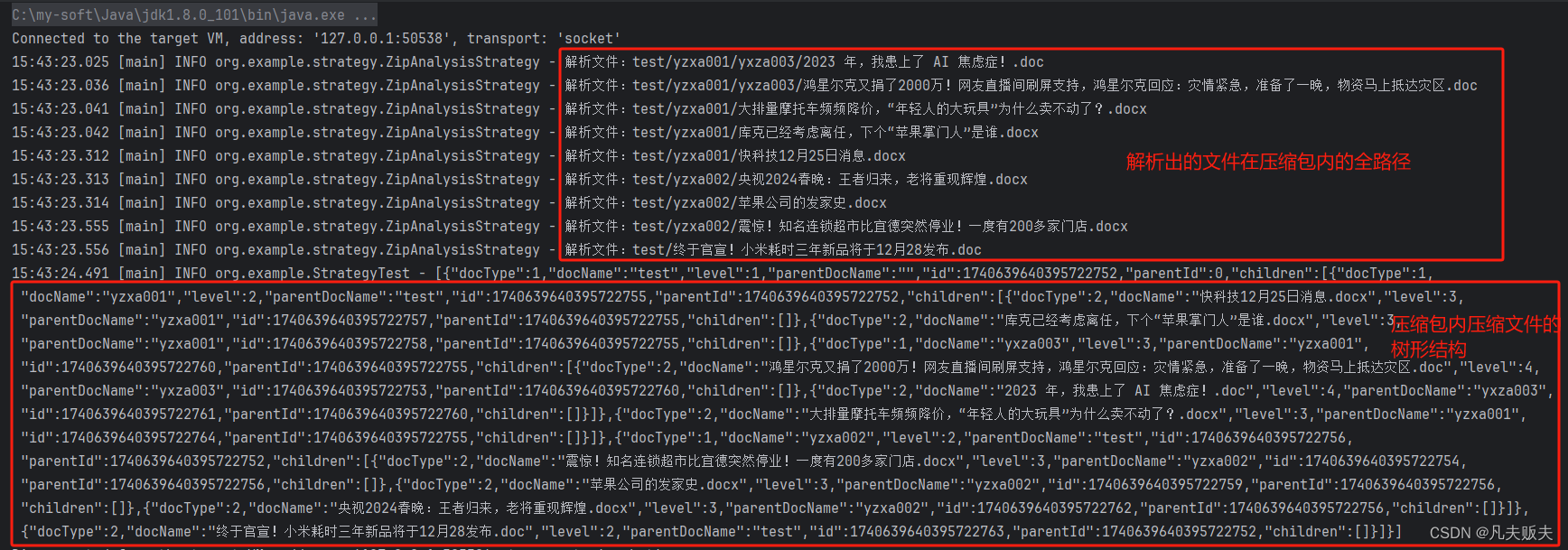
一、概念

图：记为G(V,E)

有向图：每条边都有方向

无向图：边无方向

完全图：每个顶点都与剩下的所有顶点相连

完全有向图有n(n-1)条边；完全无向图有n(n-1)/2条边

对于完全无向图，第一个节点与剩下n-1个节点相连，第二个与剩下n-2个相连……倒数第二个与最后一个相连，[(n-1)+(n-2)+......+1] = n*(n-1)/2

乘2得到完全有向图的边数

带权图：边上标有数值的图

连通图：任意两点都有路可走

要连通具有n个顶点的有向图，至少需要n条边。（构成环）

生成树：该树包含图的所有n个节点，树有n-1条边，将图连通。

如果添加一条边，必定出现环；

邻接点：一条边两端的点互为邻接点。

度：与点相连的边的条数为点的度；有向图中，从点发出的边数叫点的出度，在点终止的边数叫点的入度。

路径：从一个点沿着边走到另一个点，途径的顶点序列叫路径。

路径长度：非带权图的路径长度是指此路径上边的条数；带权图的路径长度是指路径上各边的权之和。

二、图的存储结构

2.1邻接矩阵

建立一个长和宽都为顶点数的数组，用数组元素的值表示点之间的连接情况。

无向图：

点不相连为0，相连为1
无向图邻接矩阵对称
顶点i的度 = 第i行/列中，1的个数

有向图：

不对称
元素 $a_{ij}$ 为1，表明有一条点i指向点j的边（注意方向）
顶点i的出度 = 第i行中，1的个数
顶点i的入度 = 第i列中，1的个数
顶点i的度 = 第i行和第i列中，1的个数之和

带权图：

相当于把有向图的1换为边上的值

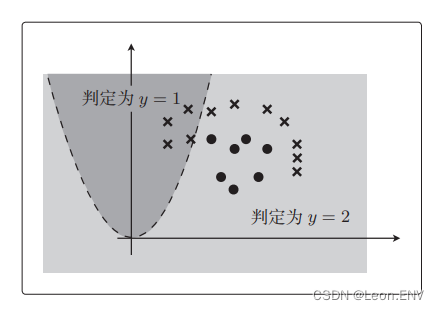
设图的邻接矩阵如下所示。各顶点的度依次是( )

A. 1 2 1 2

B. 2 2 1 1

C. 3 4 2 3

D. 4 4 2 2

答案：C 行和列的1求和

空间复杂度：n^2

代码：

int* adjacent_mat(int v, int e, int direct) 
{int* mat = (int*)malloc(sizeof(int) * v * v);  //分配空间if (!mat) return NULL;int i, start, end, weight;for (i = 0; i < v * v; i++)mat[i] = INF;           //节点全部初始化为无穷大（设无穷为65535）for (i = 0; i < e; i++)     //输入边信息{printf("输入起始 终止 权值：");scanf_s("%d %d %d", &start, &end, &weight);direct == 0 ? mat[start * v + end] = mat[end * v + start] = weight : mat[start * v + end] = weight;      //direct=0时生成无向图，对称赋值；等于1生成有向图}for (i = 0; i < v * v; i++) {mat[i] == INF ? printf("0 ") : printf("%d ", mat[i]);if ((i + 1) % v == 0)printf("\n");}return mat;
}

2.2邻接表

适用于稀疏矩阵

对每个节点建立一个链表，把与之相连的点存入节点，连接起来

一个图的邻接矩阵唯一，邻接表不唯一

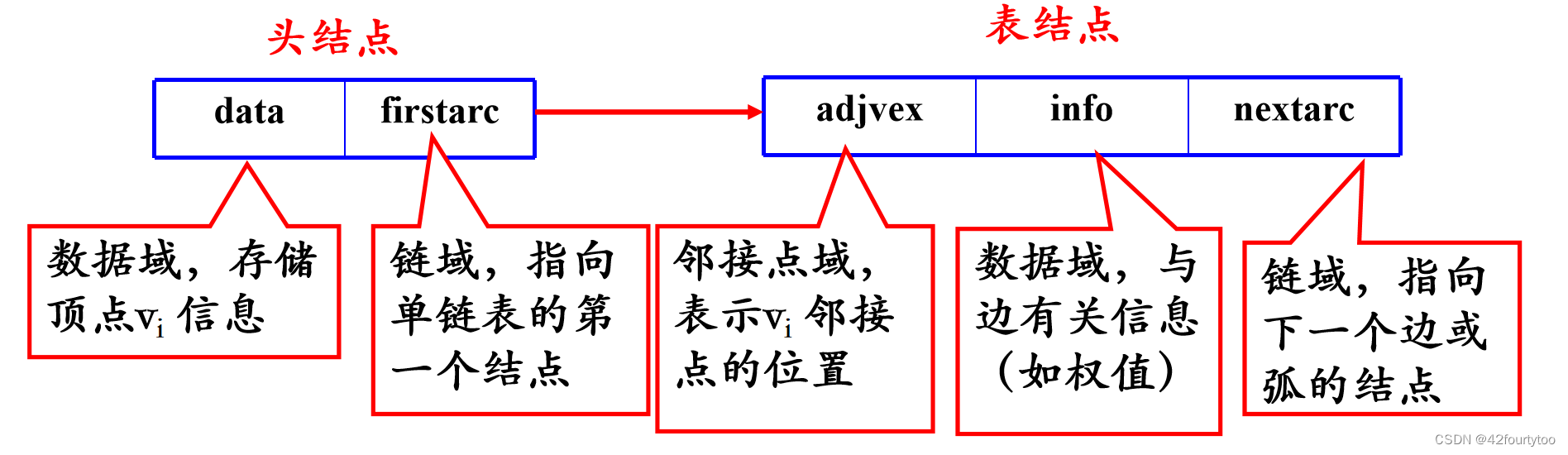
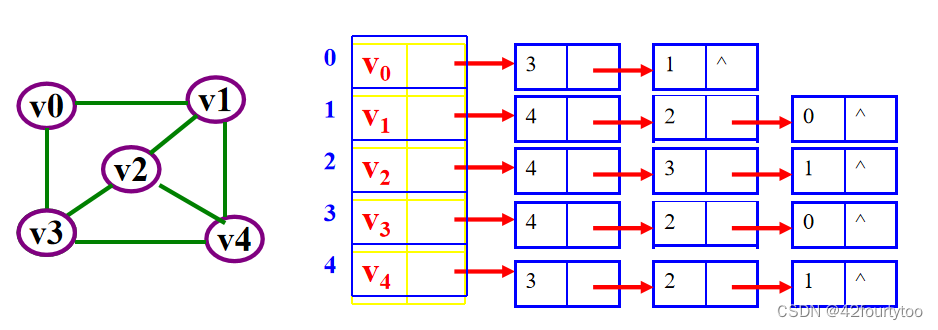
无向图的邻接表，顶点的度=该节点链表子结点个数：

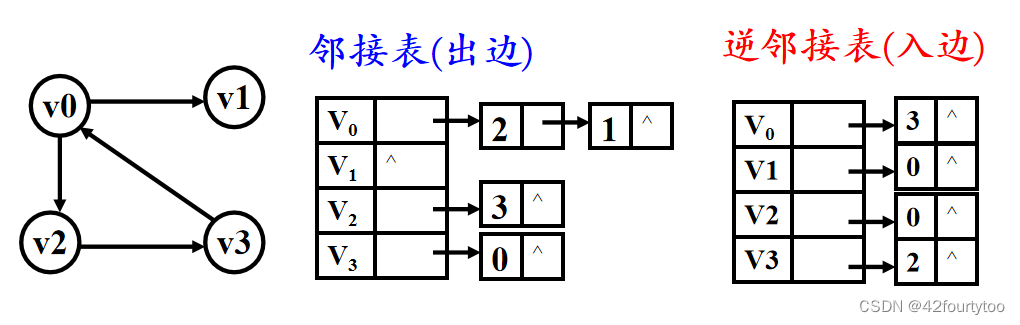
有向图的邻接表和逆邻接表：

空间复杂度(n+e) 点数加边数

代码：

node* adjacency_list(int v, int e, int direct) 
{headnode* headlist = (headnode*)malloc(sizeof(headnode) * v);if (!headlist) return NULL;int i;for (i = 0; i < v; i++) {headlist[i].data = i;headlist[i].next = NULL;}int start, end, weight;node* p, * newnode;for (i = 0; i < e; i++){printf("输入起始 终止 权值：");scanf_s("%d %d %d", &start, &end, &weight);if (direct != 2) {newnode = (node*)malloc(sizeof(node));newnode->adjvex = newnode->data = end;newnode->next = NULL;p = headlist[start].next;if (!p) {headlist[start].next = newnode;}else {while ((p->next) != NULL)p = p->next;p->next = newnode;}}if (direct == 0 || direct == 2){newnode = (node*)malloc(sizeof(node));newnode->adjvex = newnode->data = start;newnode->next = NULL;p = headlist[end].next;if (!p) {headlist[end].next = newnode;}else {while ((p->next) != NULL)p = p->next;p->next = newnode;}}}for (i = 0; i < v; i++) {printf("%d:", headlist[i].data);p = headlist[i].next;while (p) {printf("%d ", p->data);p = p->next;}printf("\n");}
}

2.3十字链表

考试没要求，先不写

三、图的遍历

图的遍历是从给定的源点出发，每个节点仅访问一次

基本算法有深度遍历和广度遍历两种

3.1深度优先DFS

沿着一条路一直走，没路了再回头找最近的分岔路口

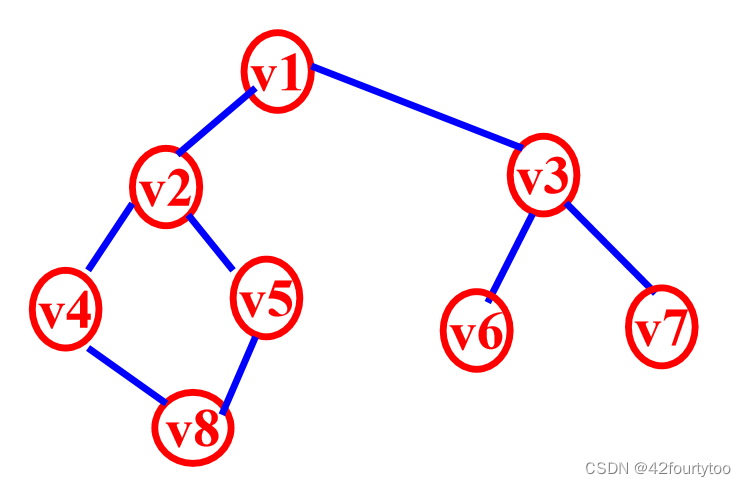
如上图，从v1开始DFS，可得到v1-v2-v4-v8-v5-v3-v6-v7

void DFS(int*mat, int v, int num, int*& visited)  //深度优先，递归版。需要传入邻接矩阵，点数，起始点编号，已访问数组
{printf("%d", num);             //输出起始节点visited[num] = 1;              //标记起始节点for (int i = 0; i < v; i++)    //在起始节点这一行从头搜索未遍历过的邻接点，进行递归if (!visited[i] && mat[num * v + i] != INF)DFS(mat, v, i, visited);	
}void DFS2(int* mat, int v) 
{int head = 0, i;int* stack = (int*)malloc(sizeof(int) * v);     //创建栈if (!stack) return;int* visited = (int*)malloc(sizeof(int) * v);   //创建标记数组，初始化为0if (!visited)  return;for (i = 0; i < v; i++)visited[i] = 0;int num;printf("输入开始节点编号：");scanf_s("%d", &num);//循环中，入栈在最后，所以先入栈一个点stack[head++] = num;      //入栈，标记, 输出visited[num] = 1;printf("%d", num);int temp;while (head)    //栈空时结束{temp = stack[head - 1];   //获取栈顶for (i = 0; i < v; i++)   //对栈顶对应的邻接矩阵所在行进行遍历，有未标记且相邻的就赋值退出，找不到则退栈{if (visited[i] == 0 && mat[temp * v + i] != INF) {temp = i;break;}}if (i == v)   //找不到退栈，找到入栈head--;else {stack[head++] = i;visited[i] = 1;printf("%d", i);}}
}void DFS3(int* mat, int v) 
{int top = -1, i;int* stack = (int*)malloc(sizeof(int) * v);     //创建栈if (!stack) return;int* visited = (int*)malloc(sizeof(int) * v);   //创建标记数组，初始化为0if (!visited)  return;for (i = 0; i < v; i++)    //标记数组初始化为0visited[i] = 0;int num;printf("输入开始节点编号：");scanf_s("%d", &num);//循环中，入栈在最后，所以先入栈一个点stack[++top] = num;      //入栈，top指向栈顶元素visited[num] = 1;        //标记int temp;while (top >= 0)    //栈空时结束{temp = stack[top];   //获取栈顶printf("%d", temp);for (i = 0; i < v; i++)   //对栈顶对应的邻接矩阵所在行进行遍历，有未标记且相邻的就赋值退出，找不到则退栈{if (visited[i] == 0 && mat[temp * v + i] != INF) {stack[++top] = i;visited[i] = 1;break;}}if (i == v)   //该节点所有相邻节点访问完毕，退栈top--;}
}

3.2广度优先BFS

访问节点，把它的子节点全部访问，再依次访问子节点的全部子节点

时间复杂度：

DFS和BFS相同：

用邻接矩阵存储时，O(n^2)

用邻接表存储时，O(n+e)

四、最小生成树

生成树：是一个极小连通子图，它含有图中全部顶点，但只有n-1条边

最小生成树：各边权值之和最小的树

4.1PRIM普利姆算法

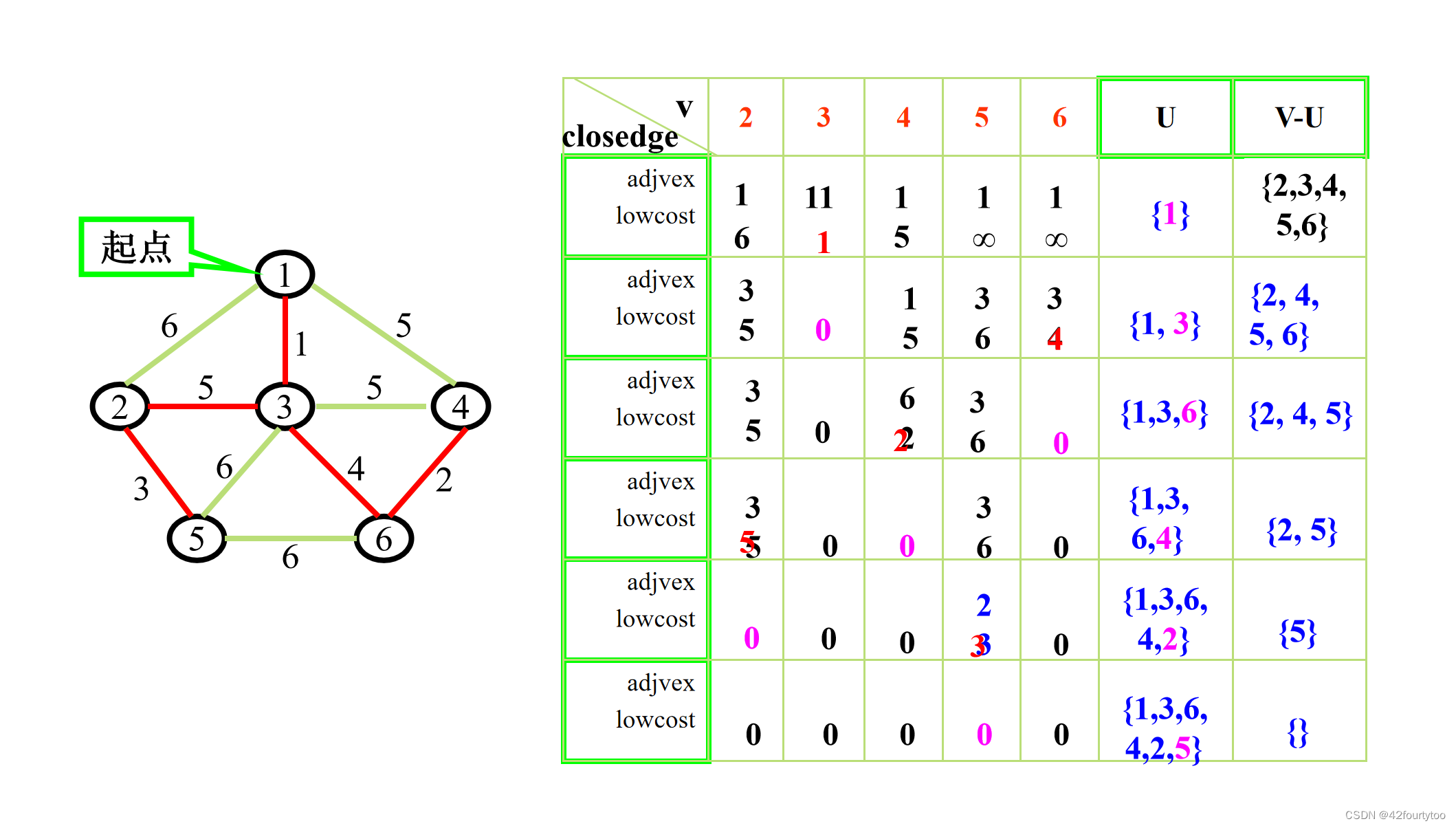
将所有点分为树U和图V两个集合，找到UV两个点集之间的权值最小边，把该边V中的点移到U里面，重复，直到V点全部到U里面

表格横表头为除起点外其他点、U集合、V-U集合；竖表头为lowcost：点到U集合的最小值，adjvex：最小值相连的点

每一次选出lowcost最小的加入U集合，然后用这个节点到其它节点的距离更新lowcost和adjvex；已确定的点写0

#include<stdio.h>
#include<stdlib.h>#define INF 65535typedef struct node {int adjvex;int data;struct node* next;
}node;typedef struct {int data;node* next;
}headnode;int* adjacent_mat(int v, int e, int direct)
{int* mat = (int*)malloc(sizeof(int) * v * v);if (!mat) return NULL;int i, start, end, weight;for (i = 0; i < v * v; i++)mat[i] = INF;for (i = 0; i < e; i++){printf("输入起始 终止 权值：");scanf_s("%d %d %d", &start, &end, &weight);direct == 0 ? mat[start * v + end] = mat[end * v + start] = weight : mat[start * v + end] = weight;}for (i = 0; i < v * v; i++) {mat[i] == INF ? printf("0 ") : printf("%d ", mat[i]);if ((i + 1) % v == 0)printf("\n");}return mat;
}void prim(int* mat, int v)   //求最小生成树。始终寻找未标记点到已标记集合的最短距离；而迪杰斯特拉是寻找未标记点到源点的最短距离
{int i, num, min, x, time = 0;int* visited = (int*)malloc(sizeof(int) * v);   //标记是否已遍历if (!visited) return;for (i = 0; i < v; i++)visited[i] = 0;int* lowcost = (int*)malloc(sizeof(int) * v);   //lowcost为未标记点到已标记点集合的最小值，from为与之连接的点的编号if (!lowcost) return;int* from = (int*)malloc(sizeof(int) * v);if (!from) return;printf("输入起始节点：");scanf_s("%d", &num);visited[num] = 1;time++;for (i = 0; i < v; i++) {lowcost[i] = mat[num * v + i];from[i] = num;}while (time != v){min = INF;for (i = 0; i < v; i++)    //找到距离最小点，传播{if (lowcost[i] < min && visited[i] != 1){min = lowcost[i];x = i;}}printf("%d-%d\n", from[x], x);visited[x] = 1;//num = x;time++;for (i = 0; i < v; i++)   //更新距离最小值if (mat[x * v + i] < lowcost[i] && visited[i] != 1) {lowcost[i] = mat[x * v + i];from[i] = x;}}
}int main() {int v, e, direct;printf("输入点数 边数：");scanf_s("%d %d", &v, &e);printf("无向图输入0，有向图输入1：");scanf_s("%d", &direct);int* admat = adjacent_mat(v, e, direct);prim(admat, v);
}

时间复杂度：O(n^2) 外层：为n个节点确定位置；内层：对于新确定的节点计算他和其他节点的距离

五、拓扑排序

1.选定一个没有直接前驱的点，输出

2.删除该起点和它相邻的边

3.重复1，2直到点全部输出，得到拓扑序列

如果还有未输出的节点，说明这些点都有直接前驱，即图中存在环

拓扑排序可以判断图是否有环

拓扑序列为：4 0 3 2 1 5

对上图进行拓补排序,可以得到不同的拓扑序列的个数是( )

答案：3

六、关键路径

顶点表示事件，有向边表示活动，边的权值表示完成活动所需时间，这样的网络叫AOE网

比如说，我们要完成一项工程，为了达到最终目标，我们要先完成许多小任务

事件最早发生时间VE：是到这一事件的最长路径。因为只有所有前期工作都做完了，这个事件才能发生，所以把前期工作完成需要的最长时间是该事件的最早发生时间。

ve(源点)=0
ve(k) = Max{ ve{j} + Weight(j, k) }, j为k的任意前提顶点, Weight(j, k)表示<j, k>边上的权值

事件的最晚发生时间VL：在完成总工程所需时间不变的情况下，一个事件最晚可以发生的时间。比如ab是c事件的前期工作，a花的时间比b长，由于c最早开始时间由最长的路径决定，所以b可以推迟一会再发生，也不会耽误总工期。

vl(汇点) = ve(汇点)
vl(k) = Min{ vl(j) - Weight(k, j) } ，k为j的任意前驱

边的最早开始时间E：即起始点的最早发生时间，事件一发生，活动就开始

边的最晚开始时间L：终点的最晚发生时间减去活动所需时间，由活动结束最晚时间倒退活动最晚开始时间

时间余量：活动的最早最晚开始时间之差，代表该活动最长拖延时间。如果该活动时间余量为0，说明为保证总时间，该活动不能拖延，称其为关键活动。把关键活动连起来得到关键路径

应用题模板：

写出点的ve和vl，边的权值、e和l

下列关于AOE网的叙述中，不正确的是（）。
A．关键活动不按期完成就会影响整个工程的完成时间
B．任何一个关键活动提前完成，那么整个工程将会提前完成
C．所有的关键活动提前完成，那么整个工程将会提前完成
D．某些关键活动提前完成，那么整个工程将会提前完成

答案：B 关键路径是网络中最长路径，表示完成工程的最短时间。关键活动延期，总工程延期；关键活动提前，总工程不一定提前，因为关键路径可能不止一条

七、最短路径

迪杰斯特拉算法

用于求一个点到其它点的最短路径

找与起点相连的节点，更新距离和路径

找距离最小的节点，将其固定，更新为起点

应用题模板：

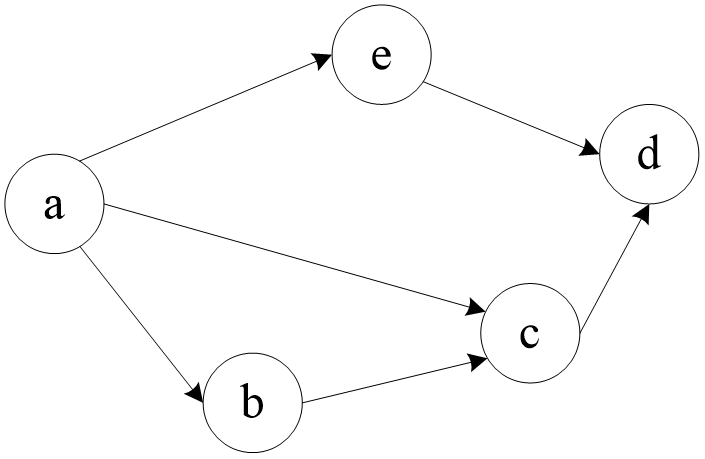
如下有向带权图,若采用迪杰斯特拉算法求源点a到其他各顶点的最短路径,得到的第一条最短路径的目标顶点是b,第二条最短路径的目标顶点是c,后续得到的其余各最短路径的目标顶点依次是（）

答案：fde

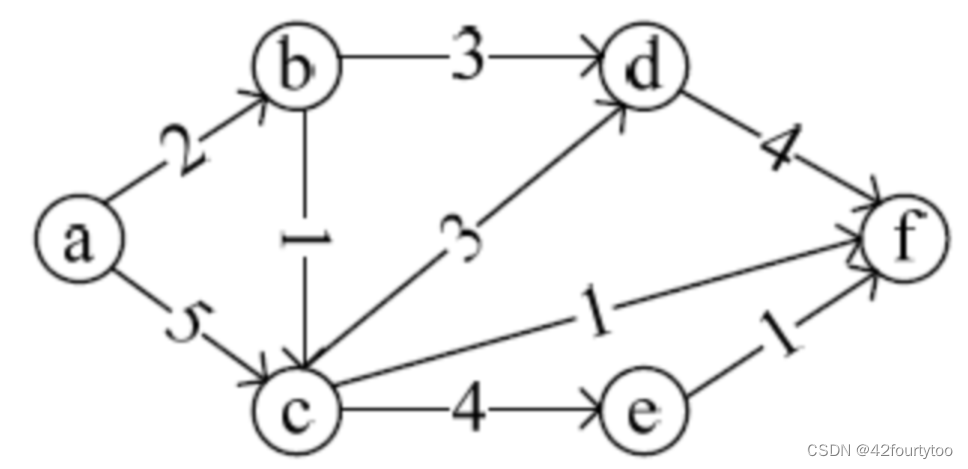
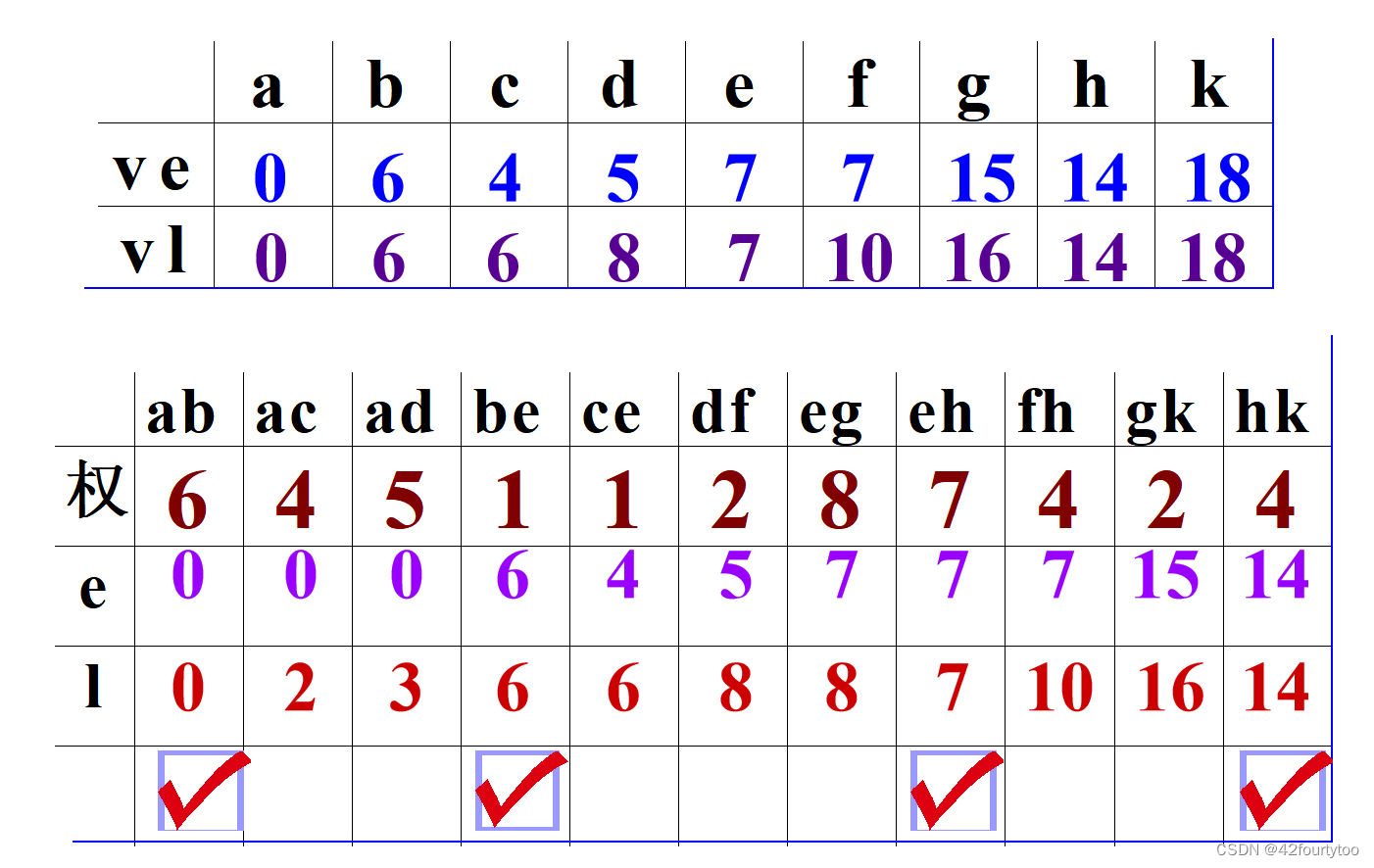
下列 AOE 网表示一项包含 8 个活动的工程。通过同时加快若干活动的进度可以缩短整个工程的工期。下列选项中，加快其进度就可以缩短工程工期的是（）

A. c 和 e

B. d 和 e

C. f 和 d

D. f 和 h

答案：C 根据图做出ve、vl表，再做出e、l表，找到关键路径。有bdcg、bdeh、bfh三条。要缩短总工期，三条关键路径都要缩短，只有C选项能同时影响三条路径。

从本题可以看出，只看点的ve=vl不能确定关键路径，必须看e=l

下列关于最小生成树的说法中，正确的是（）。

Ⅰ．最小生成树的代价唯一
Ⅱ．所有权值最小的边一定会出现在所有的最小生成树中
Ⅲ．使用普里姆（ Prim）算法从不同顶点开始得到的最小生成树一定相同
Ⅳ．使用普里姆算法和克鲁斯卡尔（ Kruskal）算法得到的最小生成树总不相同

A.仅Ⅰ

B.仅Ⅱ

C.仅Ⅰ、 Ⅲ

D.仅Ⅱ、 Ⅳ

答案：A 设想一个各边权值相等的树，则BCD错