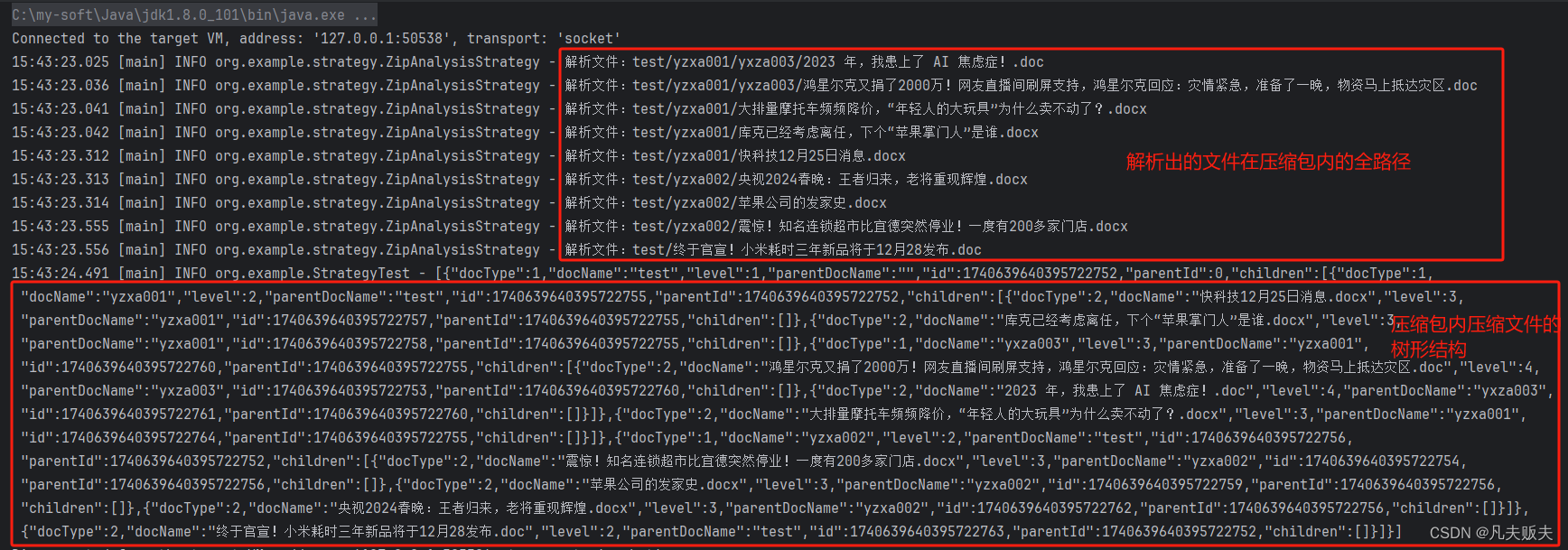
高斯分布的概率密度函数：

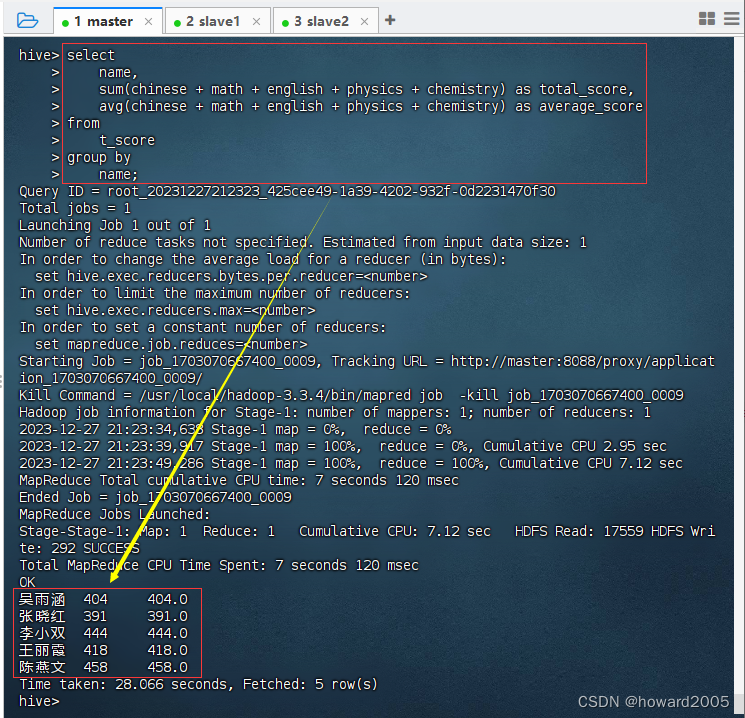
其本质问题可抽象为：已知两个独立高斯分布，$N1\sim (u1,\delta 1^2)，N2\sim (u2,\delta 2^2)$，求新的概率分布$N=N1\times N2$，通过Matlab数值计算看看两独立概率分布的乘积情况：

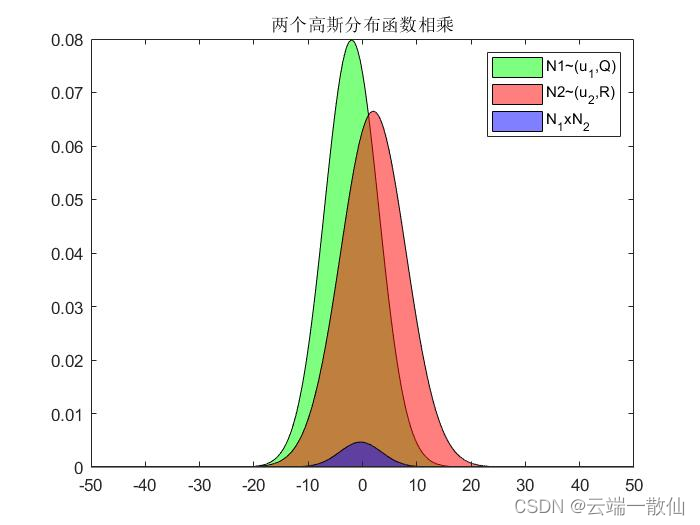
如图所示绿色和红色分别代表两个独立的高斯分布函数，蓝色为两个分布的乘积，从蓝色形状可以粗略的看出乘积结果可能为一个幅值被压缩的高斯分布，其期望在$[u_1,u_2]$之间，但是真实是否如此还需理论推导。
$N_1$的概率分布函数为$f_1(x)$，$N_2$ 的概率分布函数为$f_2(x)$ 则：

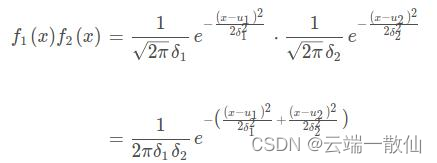
可以直接先单独分析指数部分，设：

设$\lambda$如上所示，则$\beta =\gamma +\lambda$,其中$\gamma$为一个$N\sim (u,{\delta }^2)$的正态分布，$\lambda$为一个常数值。继续简化$\lambda$，如下：

则可得两个高斯分布相乘为：

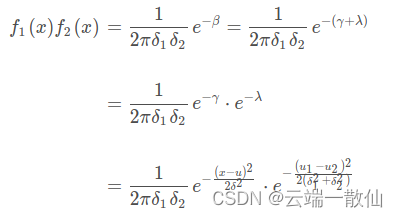
其中：

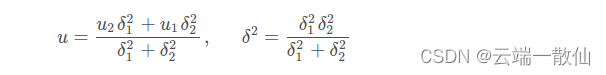
把常数项综合为$S_g$可得其直观表达方式：

两个高斯分布相乘的分布函数即推导出来，即相乘后的分布函数为一个被压缩或者放大的高斯分布，$S_g$为缩放因子，相乘后的概率密度的积分不等于1，但其方差和均值性质不变，所以 $N=N_1\times N_2\sim (u,{\delta }^2)$，也就是我们常说两个高斯分布相乘同样服从高斯分布。
关于缩放因子$S_g$。可以看出，
① 当$S_g<1$时，概率分布被压缩；
② 当 $S_g>1$ 时，概率分布被放大；
平时我们大多数情况下会看到情况①，那什么情况下才能出现情况②呢？？？
进行如下分部分析：

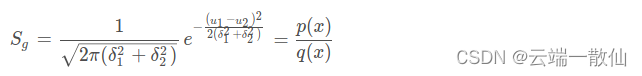
其中：

可以很容易的得到$p(x)>0,q(x)>0$，当$S_g<1$时，$p(x)<q(x)$, 当$S_g>1$时，$p(x)>q(x)$, 因此这里问题转化为判断$p(x),q(x)$的大小。
设自变量$x={\delta }_1^2+{\delta }_2^2$，$N=(u_1-u_2{)}^2$，则$x>0，N>0$

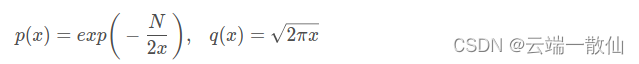
仿真计算 ：$q(x)$是条固定的曲线，$p(x)$是根据N移动的曲线蔟，大多数情况会出现$p(x)<q(x)$（情况①）

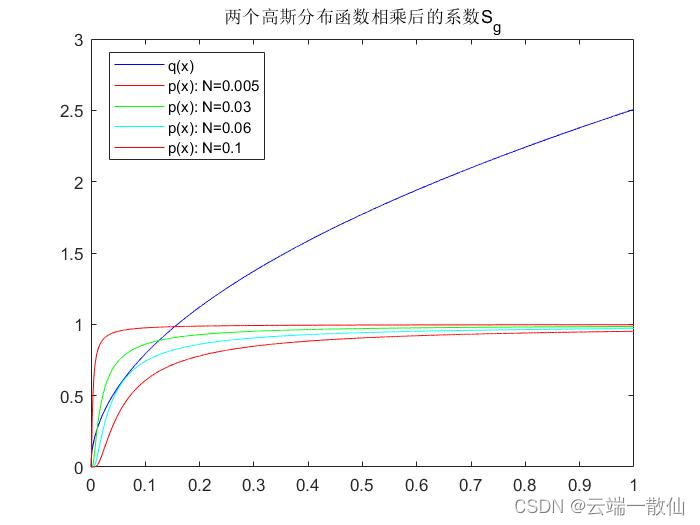
可以看出当$p(x),q(x)$只有一个交点时，即是一个情况②可能出现的临界，(这个临界$N_k$仿真差不多在0.06附近，暂且就这样认为吧)，$N$越小曲线越靠右，就会出现局部$p(x)>q(x)$的情况。
可以得出如下结论：
当$N>0.06$时，不可能出现情况②
当$0<N<0.06$时，且$a<x<b$（其中$a，b$为两交点，$a>0,b<\frac{1}{2\pi }$），出现情况②
我们手动仿真了一些情况，如下

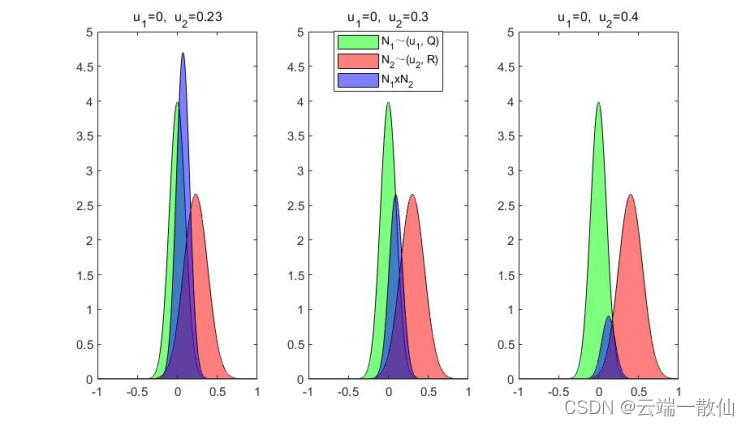
当可以通过$S_g$来判断当前的融合概率是否是被增强还是削弱时，我们是否也可以同时用来判断融合的有效性。在机器人定位中，利用Kalman融合后，可以利用$S_g$判断定位融合是否有效。

• 预测和测量相差很远时，$S_g$就变小，融合分布概率分散，真实位置概率变小；
• 预测和测量相差很近时，且方差很小时，融合分布概率更集中，真实位置概率变大
  如此我们可以设置一个阈值来判断当前融合的有效性。