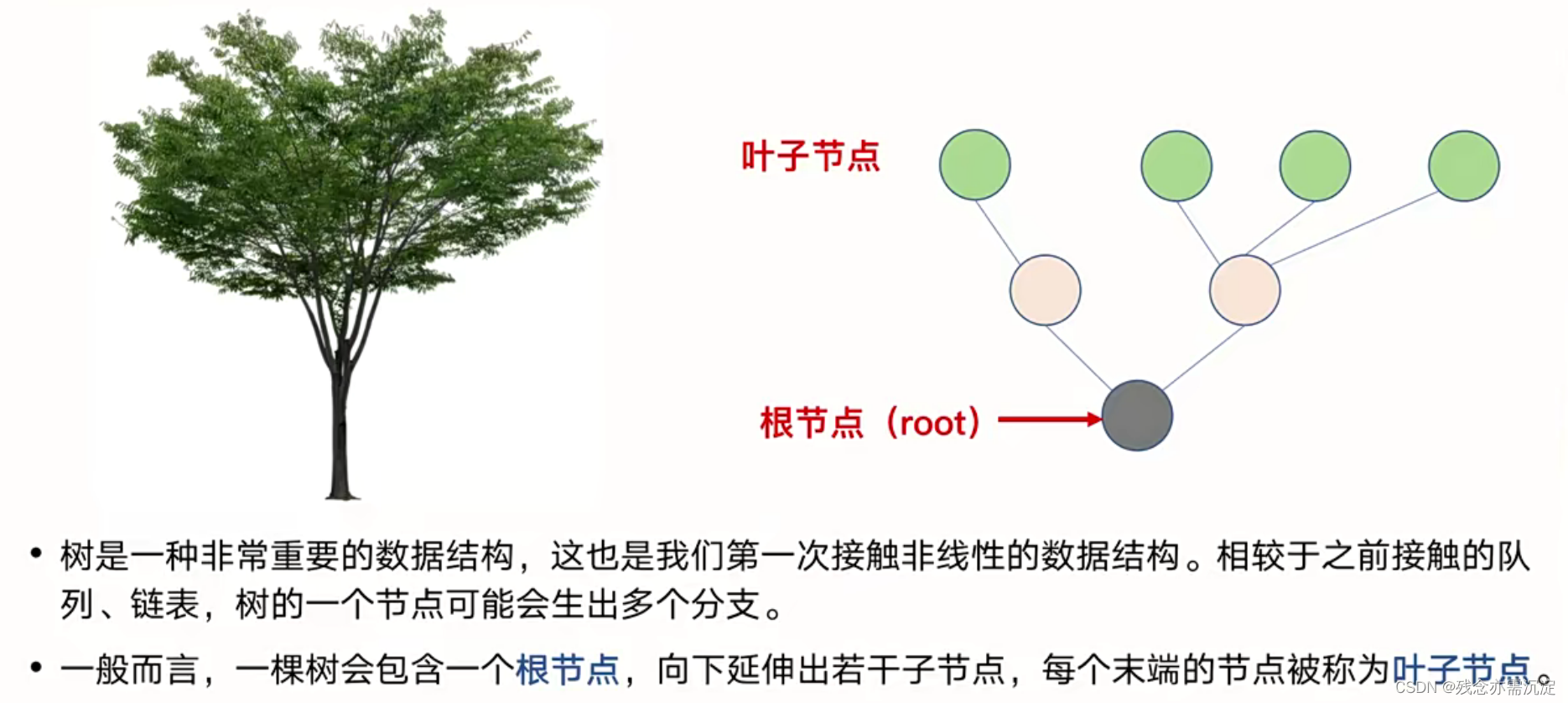
树的简介:
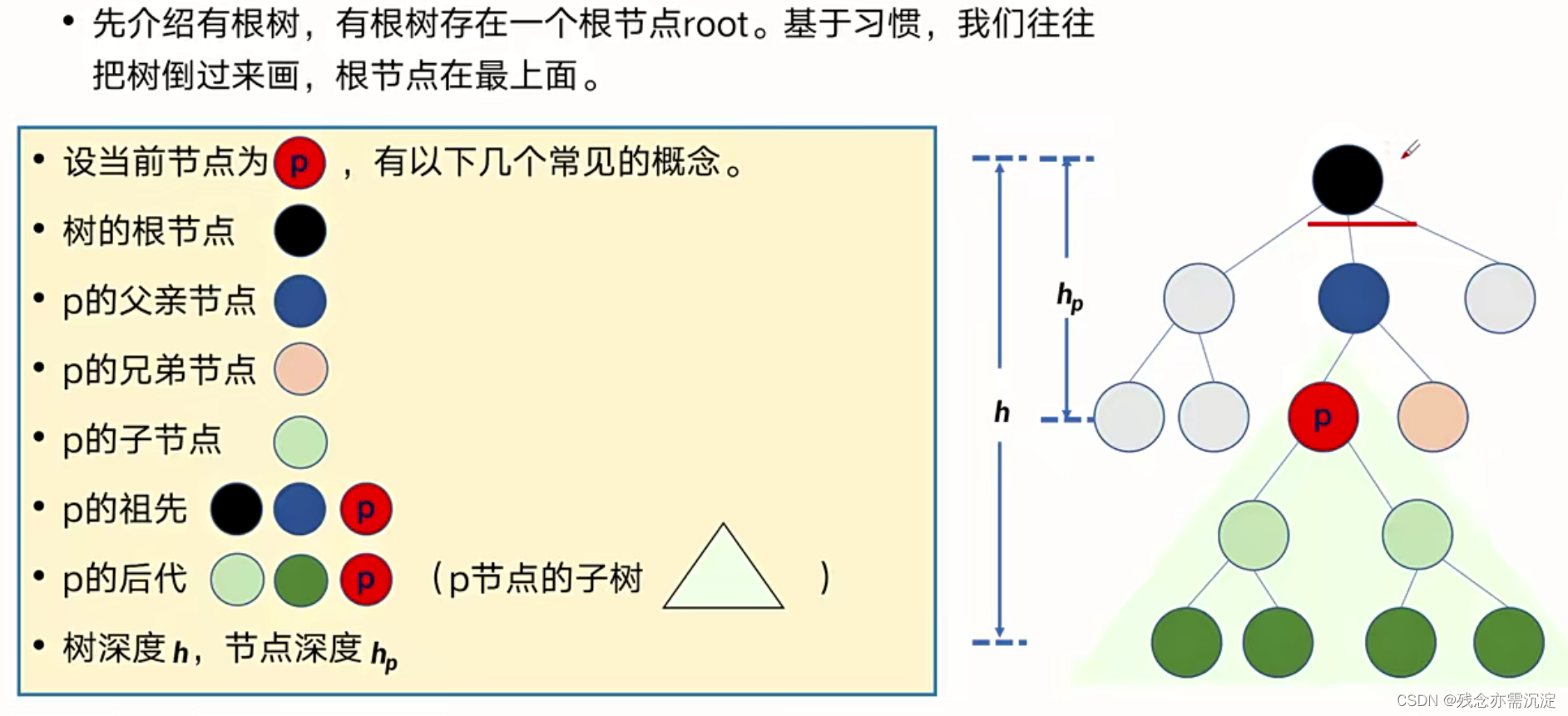
再来看看二叉树的简介:
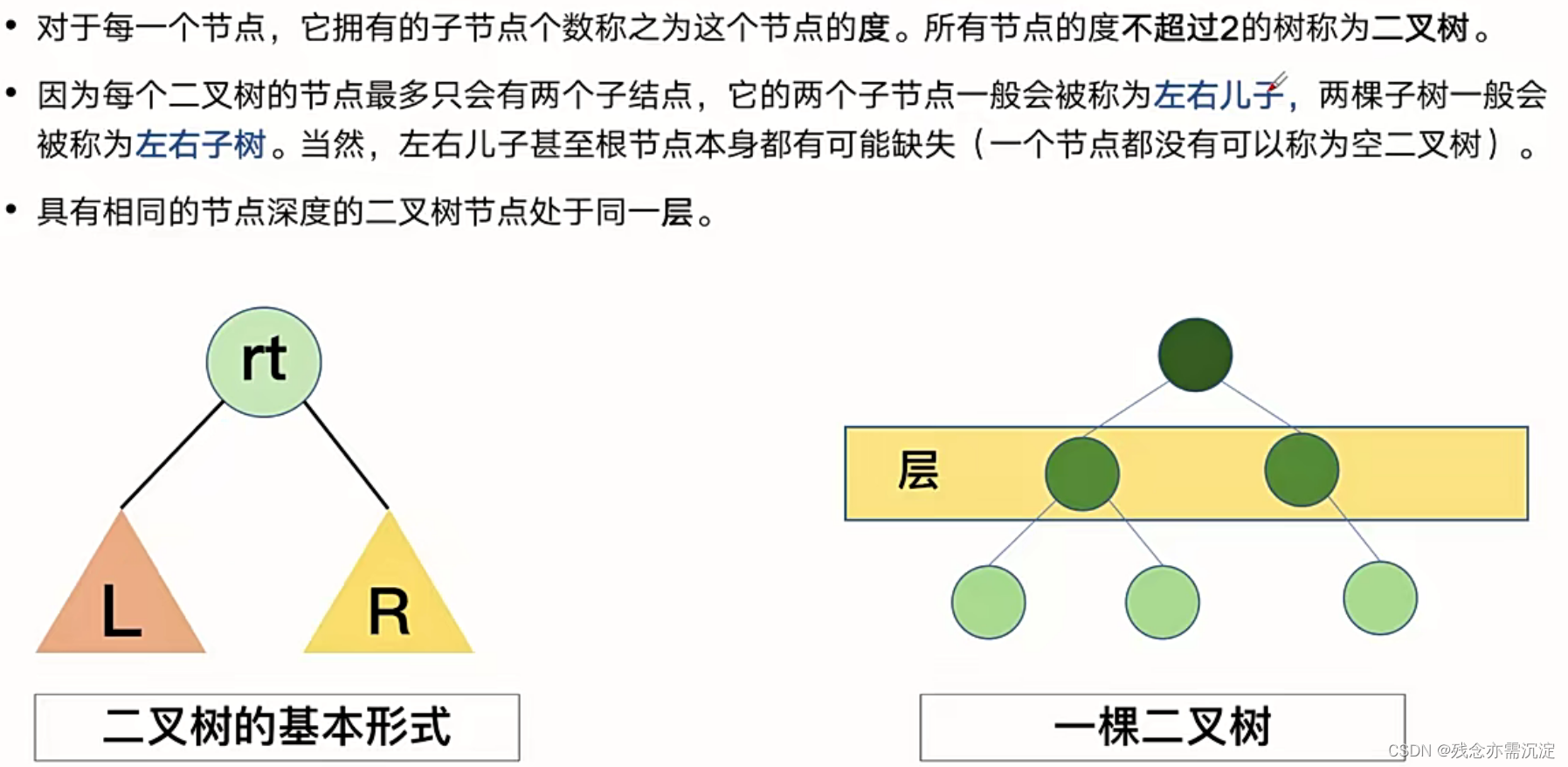
容易想到p叉树就是每个节点最多有p个子节点的树。
接下来看两种特殊的二叉树:
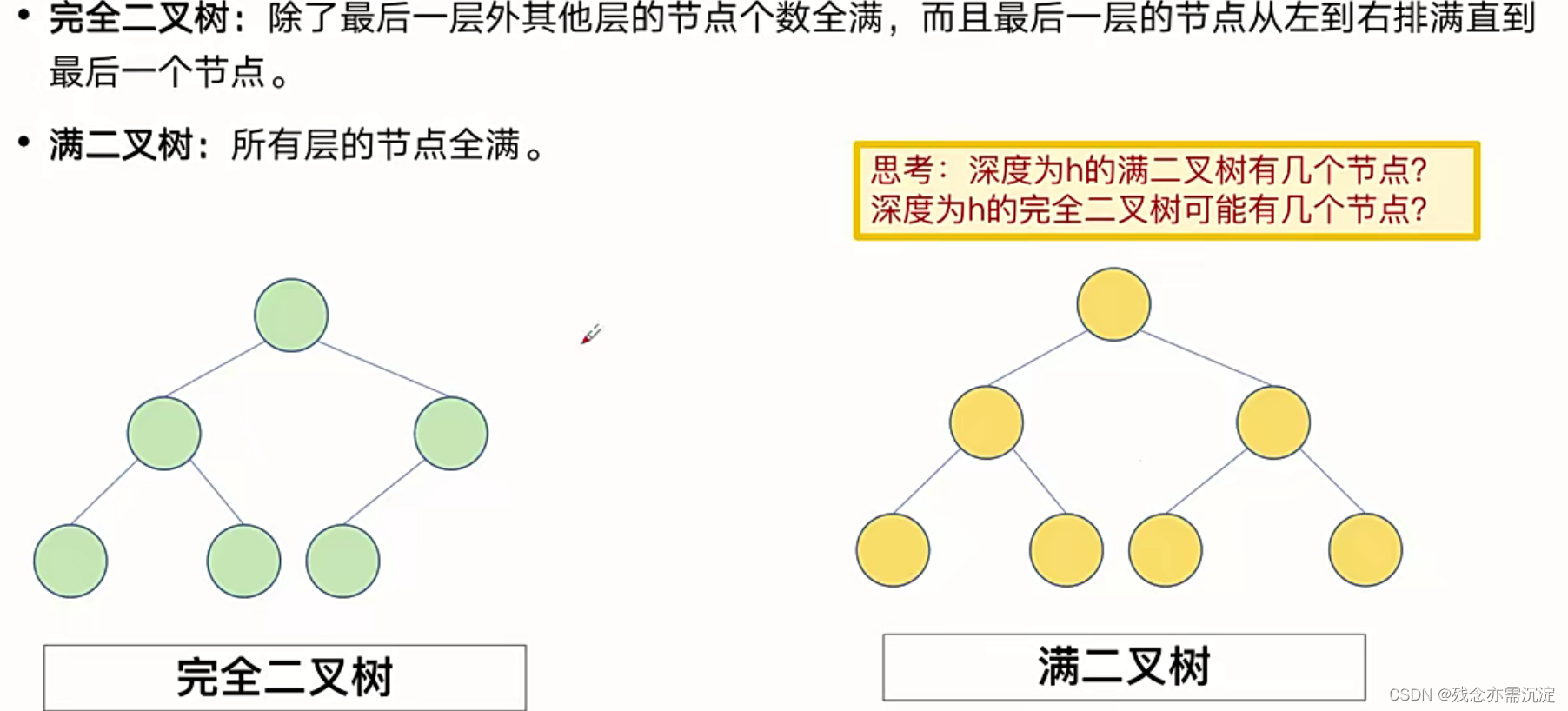
接下来我们思考两个问题:
1.深度为h的满二叉树一共有多少个节点?
对于这一个问题,我们观察满二叉树的结构,会发现最后的答案等于2^0+2^1+2^2+...+2^(h-1)=2^h-1
2.深度为h的完全二叉树的节点数范围是多少?
根据完全二叉树的定义可以知道它最后一层上面的所有部分都满足满二叉树的特征并且最后一层具有一个分界点,分界点的左边节点全部都是存在的而分界点的右边一个节点都没有 。
所以我们可以知道,深度为h的完全二叉树最小节点数为2^0+2^1+2^2+...+2^(h-2)=2^(h-1) -1+1。
而其最多的节点数和满二叉树是一样的。
接下来看完全二叉树的存储与建立:
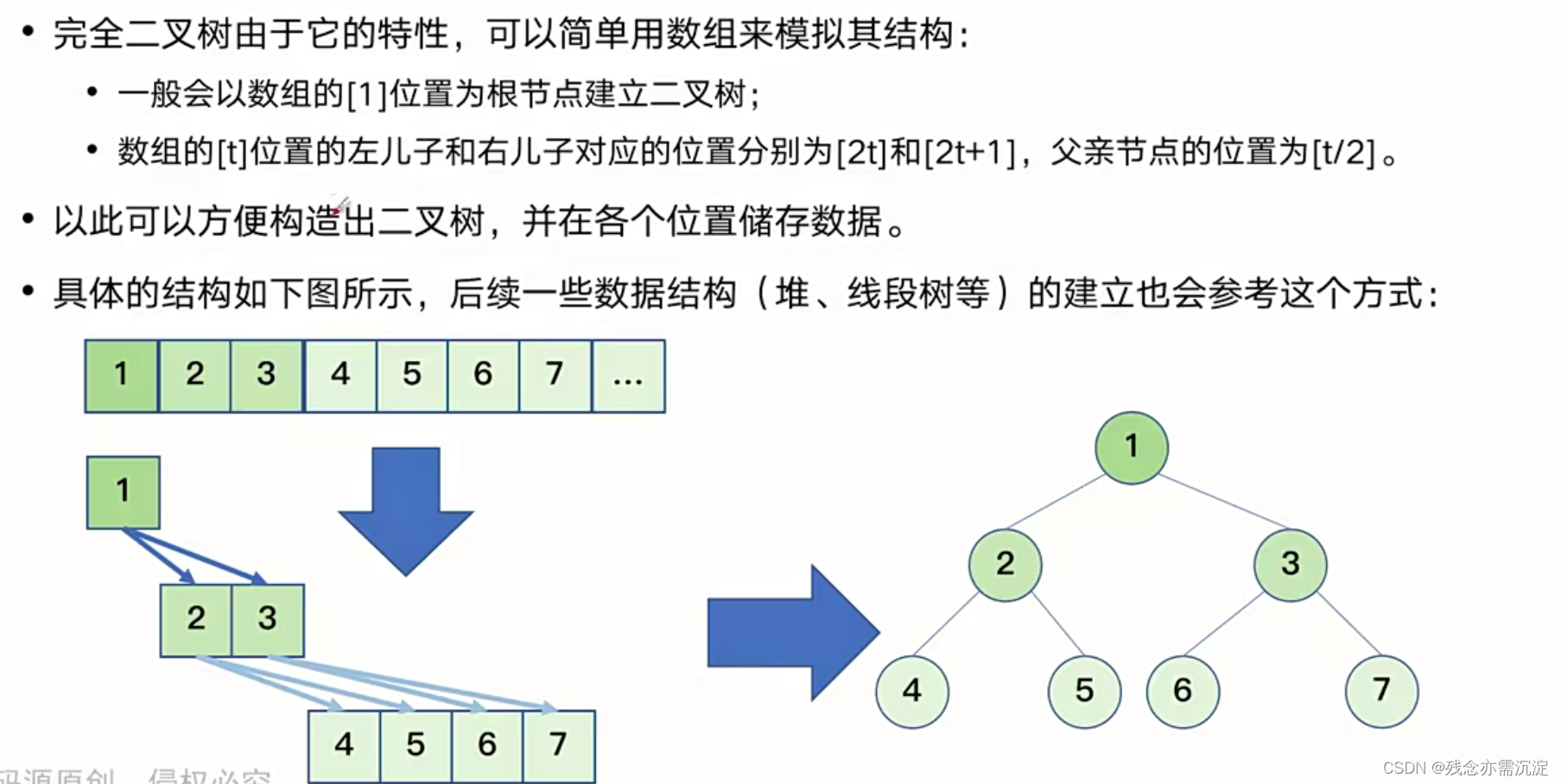
接下来是完全二叉树的建立:
通常我们是通过递归的方式对完全二叉树进行建立:
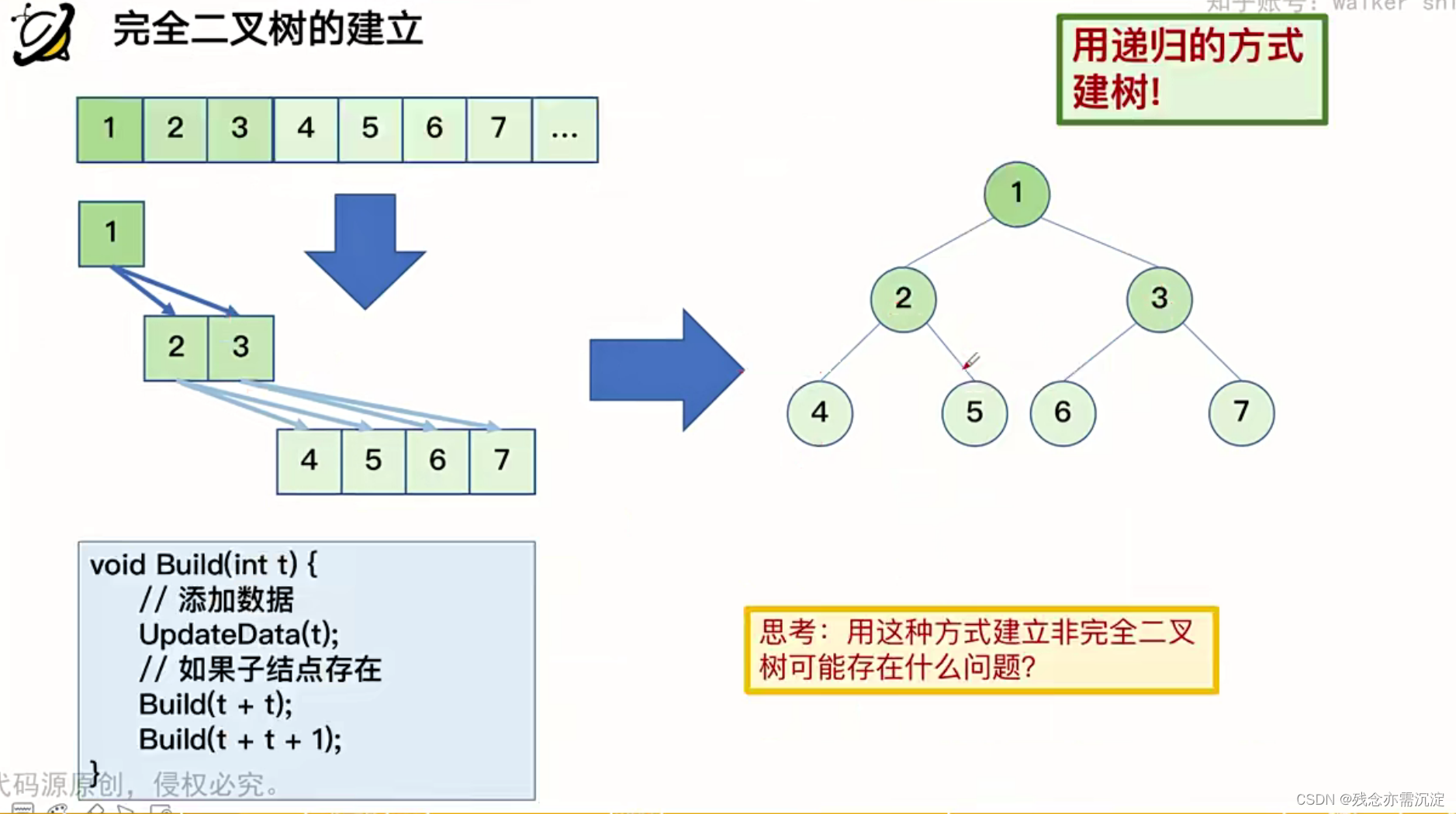
上述蓝色部分的代码就是用以建立一个以t节点为根的子树。
需要注意的是如果用这种方式想去建一个非完全二叉树的话将会导致数组中部分下标的浪费,因为对于一个确定的节点只能建立下标为它左右儿子节点的子节点,而不能保证与他下标相邻的树的节点的建立。所以我们可以知道,是否可以用这样建立树的方式去解决问题取决于问题本身,如果浪费了空间并不影响问题的解答,那么就可以用这样的方法去解答,反之则不可以。
接下来看一下一般二叉树的存储:
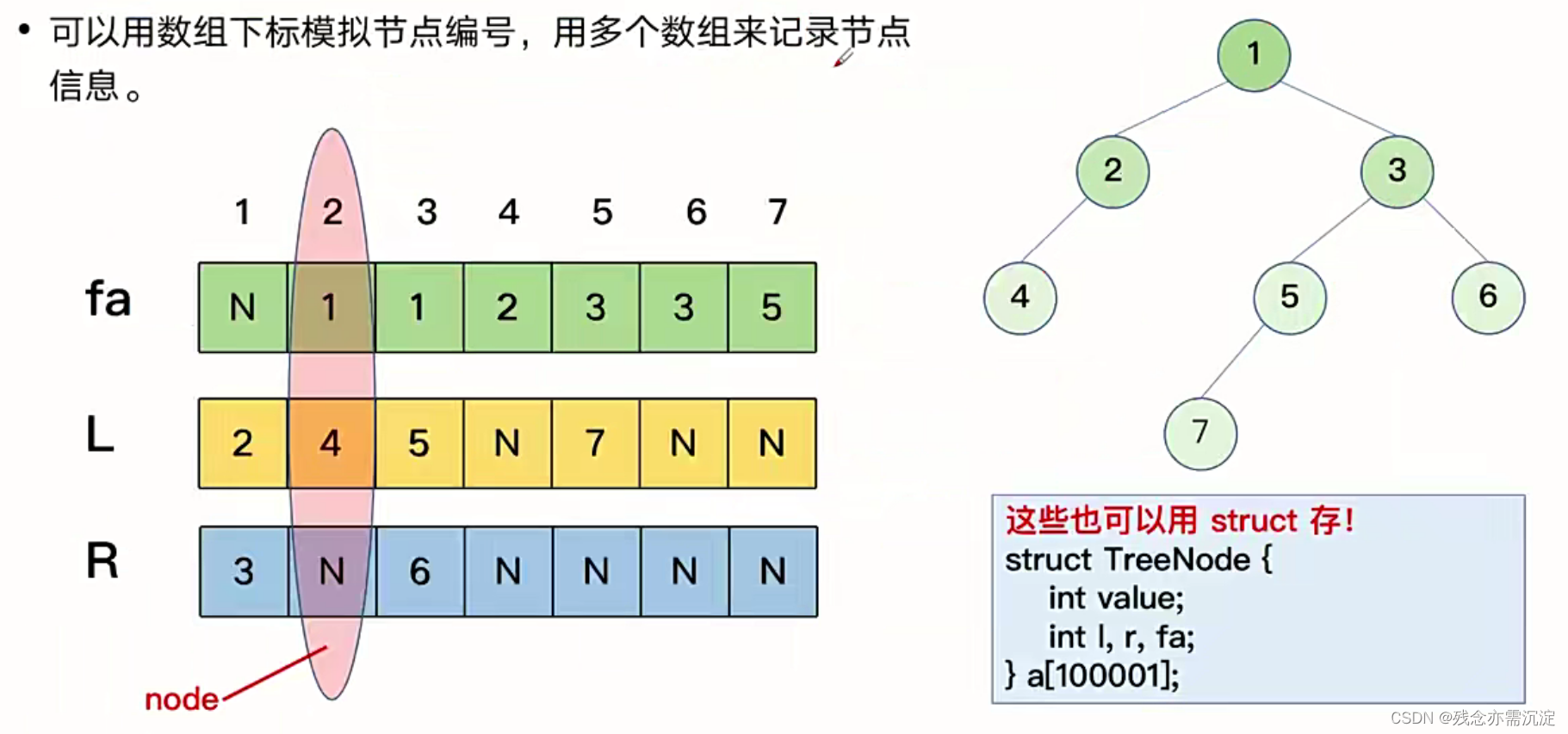
为了解决建立一个非完全二叉树,达到不浪费太大空间的目的,衍生出了一般二叉树的存储方法:
同样的我们可以考虑用指针来存储二叉树:

所以我们可以总结一下二叉树的基本操作有:
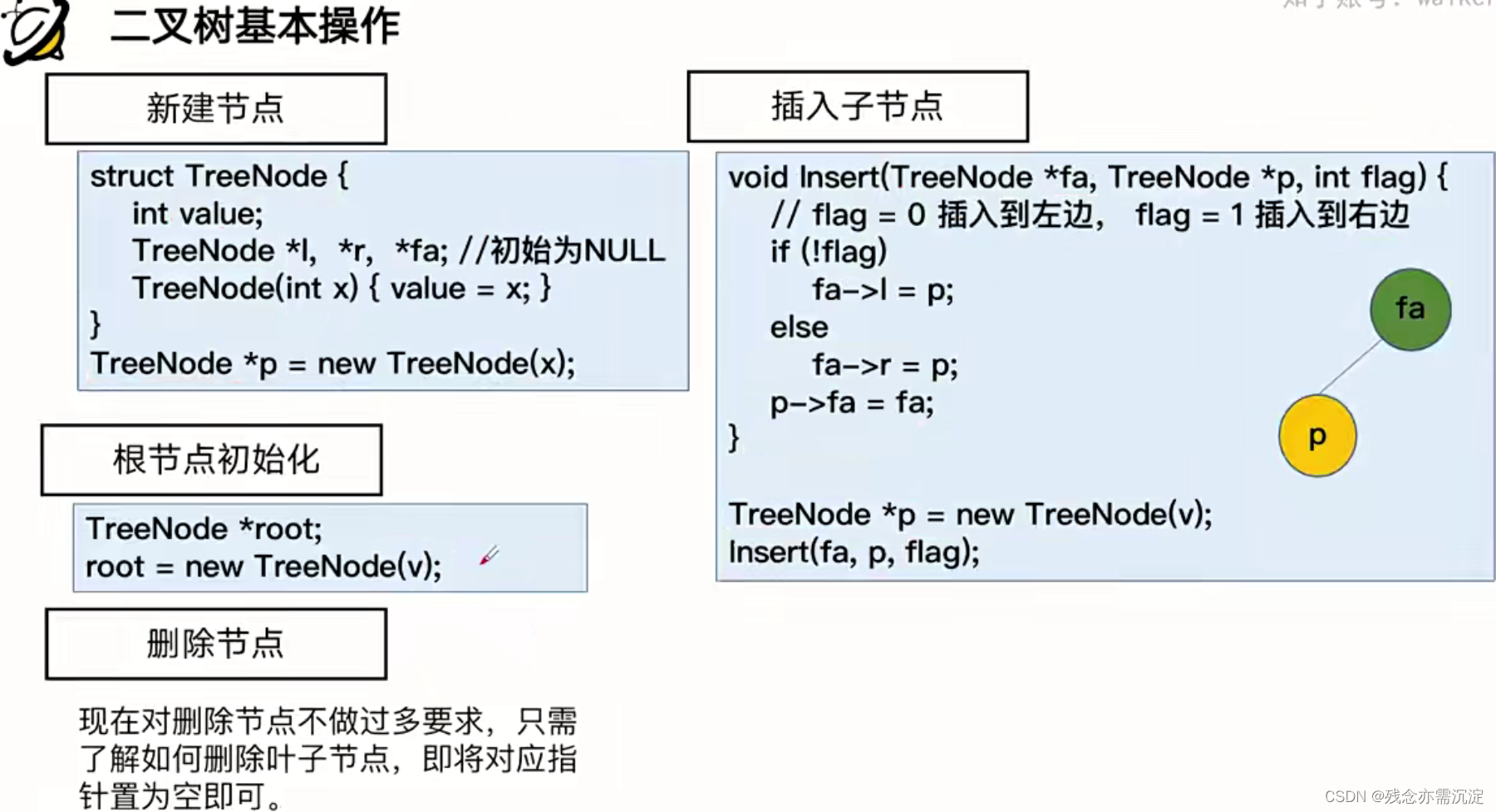 二叉树的遍历顺序:
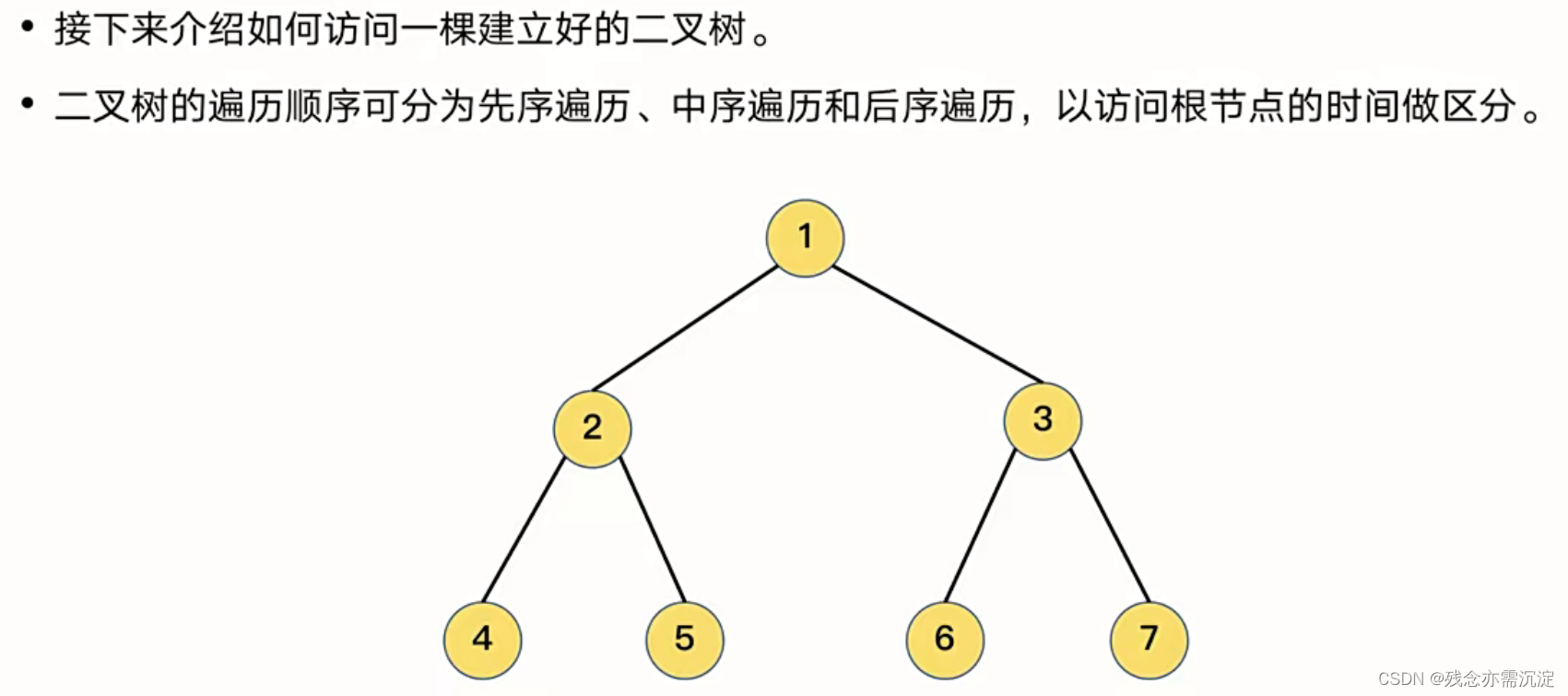
二叉树的遍历顺序:
首先是先序遍历(根左右):
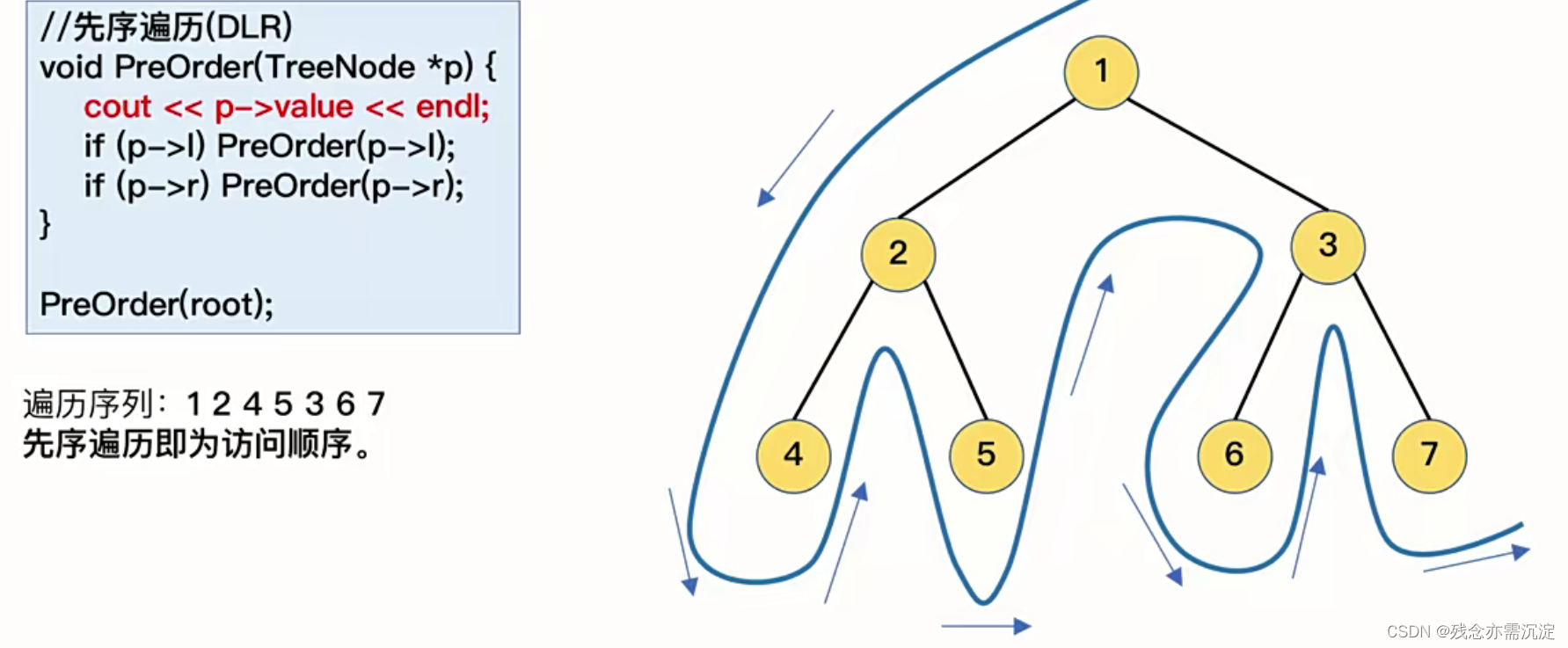
可以看出这样的遍历方式是通过递归的方式实现,从根节点开始进行递归,根据每个节点是否存在左右节点来依次遍历,同时先遍历左然后遍历右。
接下来看中序遍历(也称为左根右):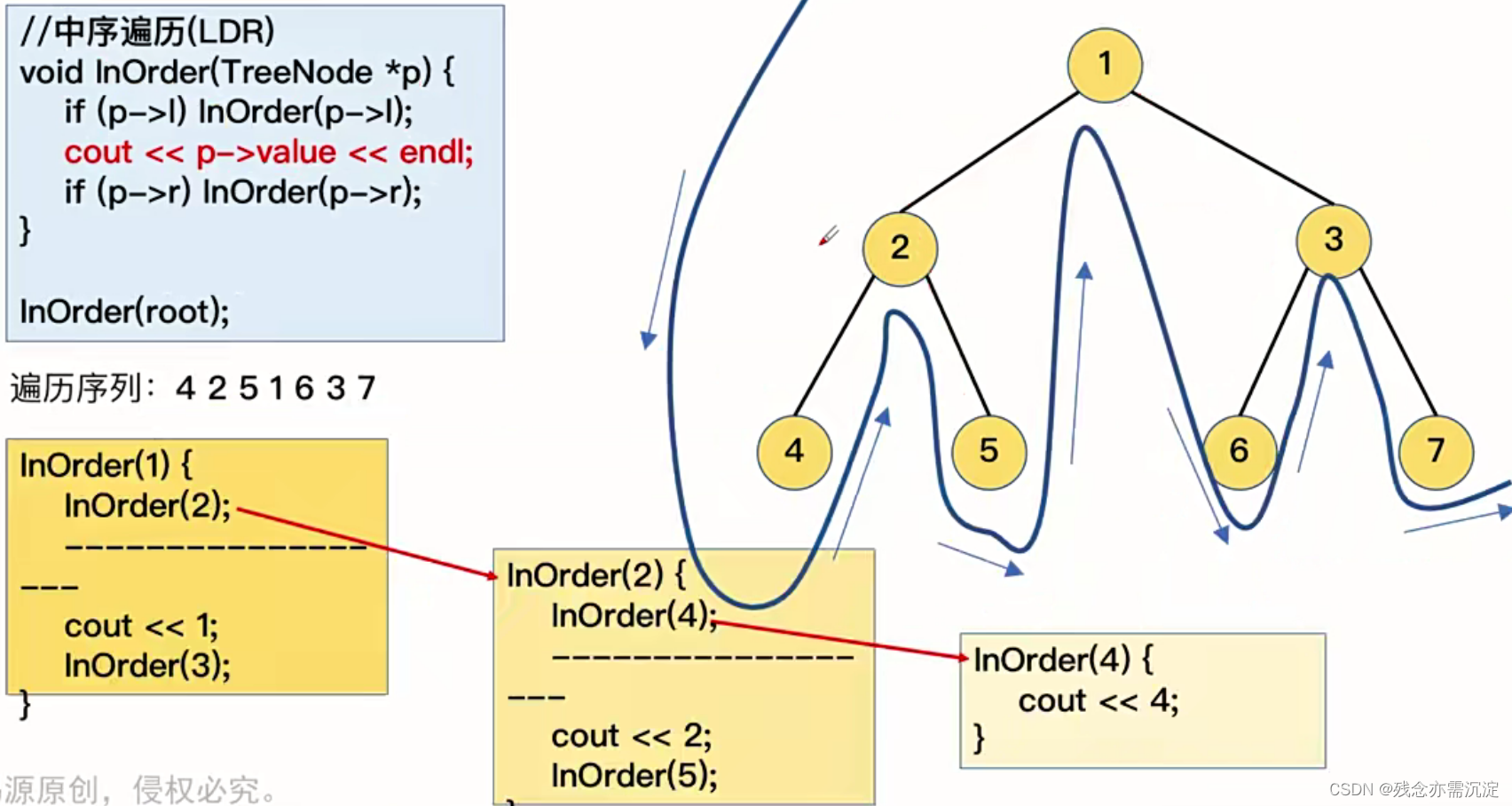
给我的感觉其实就像是以最开始的p节点开始一直先递归左节点然后反正输出,同时在反着输出的过程中如果相应左节点存在右节点,也会进行输出,文字不是很好表达,读者可以仔细去理解。
最后再来看一下后序遍历(左右根):
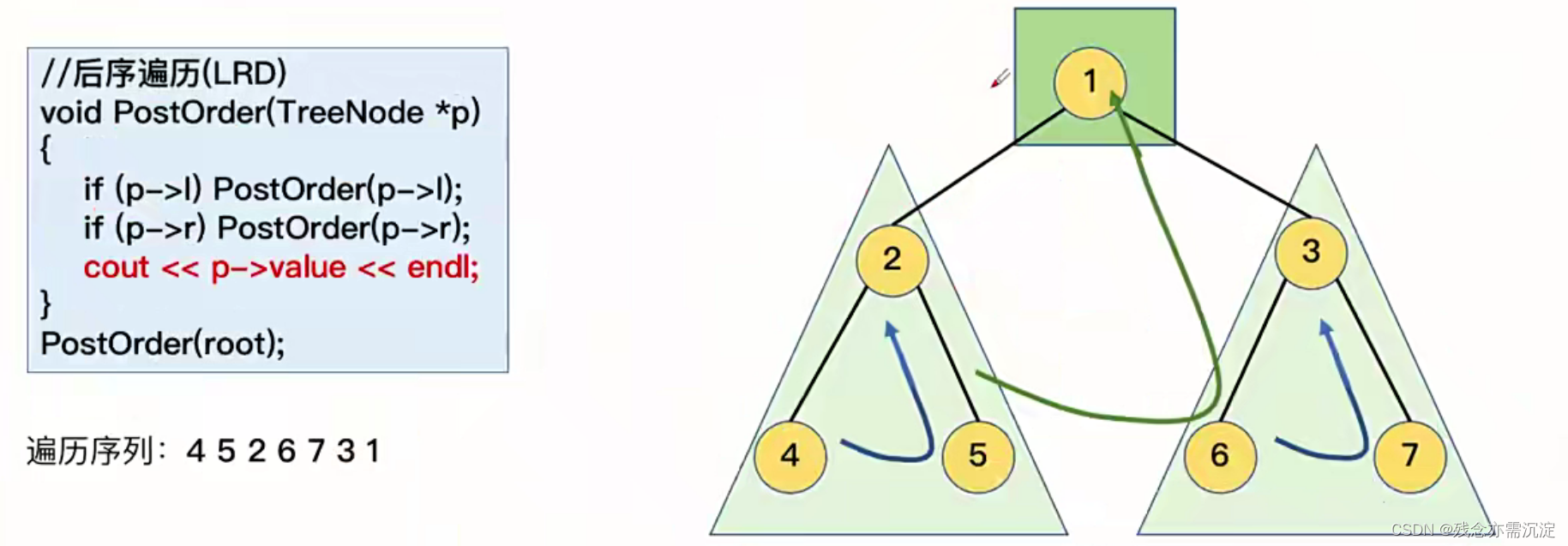
可以看出来这样的遍历顺序就是先从节点p开始,然后依次枚举其左右节点并使用递归的方式枚举到底,最后当不存在子节点的时候就进行输出。
接下来还有一种遍历叫做层级遍历:
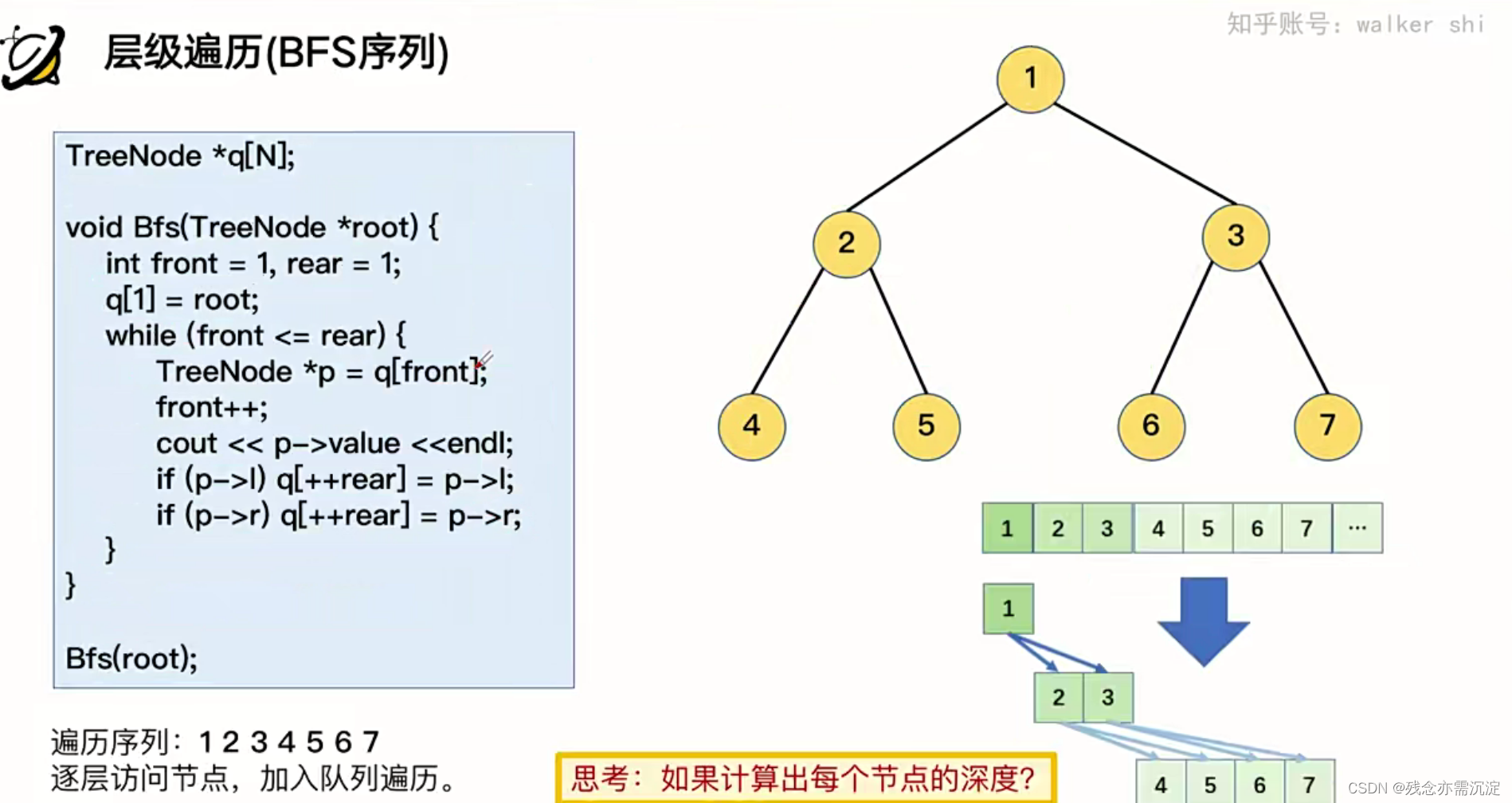
BFS(也叫做宽度优先搜索),这里蕴含了该种搜索的思想:
严格来说,在层级遍历中,我们只需要按照从上往下的顺序遍历所有点,同一层的点的先后顺序不做要求;简单来说,层级遍历指的是我们按深度从小到大的顺序一层层遍历所有点。
接下来就是运用二叉树的基本知识去解答的几道帮助巩固学习的例题:
1.遍历完全二叉树:

代码如下:
#include<bits/stdc++.h>
using namespace std;
int n;
inline void preorder(int x){cout<<x<<' ';if(x+x<=n) preorder(x+x);if(x+x+1<=n) preorder(x+x+1);
}
inline void inorder(int x){if(x+x<=n) inorder(x+x);cout<<x<<' ';if(x+x+1<=n) inorder(x+x+1);
}
inline void postorder(int x){if(x+x<=n) postorder(x+x);if(x+x+1<=n) postorder(x+x+1);cout<<x<<' ';
}
int main(){cin>>n;preorder(1);cout<<endl;inorder(1);cout<<endl;postorder(1);cout<<endl;return 0;
}其中的inline的作用解释如下:

2.遍历一般二叉树:

给出两种方法解答,以下是第一种方法的代码:
#include<bits/stdc++.h>
using namespace std;
int n;
struct treenode{int l,r,fa;
}a[1010];
inline void preorder(int x){cout<<x<<' ';if(a[x].l) preorder(a[x].l);if(a[x].r) preorder(a[x].r);
}
inline void inorder(int x){if(a[x].l) inorder(a[x].l);cout<<x<<' ';if(a[x].r) inorder(a[x].r);
}
inline void postorder(int x){if(a[x].l) postorder(a[x].l);if(a[x].r) postorder(a[x].r);cout<<x<<' ';
}
int main(){cin>>n;for(int i=1;i<=n;i++){int x,y;cin>>x>>y;if(x) a[i].l=x;if(y) a[i].r=y;a[x].fa=a[y].fa=i;}preorder(1);cout<<endl;inorder(1);cout<<endl;postorder(1);cout<<endl;return 0;
}第二种使用指针的方法来解答本题:
#include<bits/stdc++.h>
using namespace std;
int n;
struct treenode{int value;treenode *l,*r,*fa;
}a[1100];
inline void preorder(treenode *t){if(t->value) cout<<t->value<<' ';if(t->l) preorder(t->l);if(t->r) preorder(t->r);
}
inline void inorder(treenode *t){if(t->l) inorder(t->l);cout<<t->value<<' ';if(t->r) inorder(t->r);
}
inline void postorder(treenode *t){if(t->l) postorder(t->l);if(t->r) postorder(t->r);cout<<t->value<<' ';
}
int main(){cin>>n;for(int i=1;i<=n;i++){int x,y;cin>>x>>y;a[i].value=i;if(x) {a[i].l=&a[x];a[x].fa=&a[i];}if(y){a[i].r=&a[y];a[y].fa=&a[i]; }}preorder(&a[1]); cout<<endl;inorder(&a[1]);cout<<endl;postorder(&a[1]);cout<<endl;return 0;
}其实本题完全不用使用第二种方法进行解答,只是单纯的练习一下指针的使用来解答这道题。
3.二叉树的最近公共祖先:

这个题的思路就是利用两个数组来分别存储u与v的祖先,最后存储的祖先一定就是根,所以最开始出现的一样的祖先就是要输出的,代码如下:
#include<bits/stdc++.h>
using namespace std;
int n;
struct treenode{int l,r,fa;
}a[1001];
int c[1001],d[1001];
int main(){cin>>n;for(int i=1;i<=n;i++){int x,y;cin>>x>>y;if(x){a[i].l=x;a[x].fa=i;}if(y){a[i].r=y;a[y].fa=i;}}int l1,l2;l1=l2=0;int u,v;cin>>u>>v;while(u!=1){c[++l1]=u;u=a[u].fa;}c[++l1]=1;while(v!=1){d[++l2]=v;v=a[v].fa;}d[++l2]=1;int x;for(int i=l1,j=l2;j&&i;j--,i--){if(c[i]==d[j]) x=c[i];else break; }cout<<x<<endl;return 0;
}这种做法相对来说比较容易并且也比较容易理解。最后的x就是答案,他就是c,d数组从根往下看,最后一个相同的值,这也就是u和v的最近公共祖先。
接下来再提供一种更为复杂的做法,也就是按层级遍历的方法来写:
#include<bits/stdc++.h>
using namespace std;
int n,q[1025];
struct treenode{int depth;int l,r,fa;
}a[1025];
int main(){cin>>n;for(int i=1;i<=n;i++){int x,y;cin>>x>>y;if(x){a[i].l=x;a[x].fa=i;}if(y){a[i].r=y;a[y].fa=i;}}int front,rear;front=rear=1;q[1]=1;a[1].depth=1;while(front<=rear){int p=q[front];++front;if(a[p].l){q[++rear]=a[p].l;a[a[p].l].depth=a[p].depth+1;}if(a[p].r){q[++rear]=a[p].r;a[a[p].r].depth=a[p].depth+1;}}int u,v;cin>>u>>v;if(a[u].depth<a[v].depth)swap(u,v);int x=a[u].depth-a[v].depth;for(int i=1;i<=x;i++)u=a[u].fa;while(u!=v){u=a[u].fa;v=a[v].fa;}cout<<u<<endl;return 0;
}4.二叉树节点子树和:

注意到有两个数据范围,如果是较小的,那么:
#include<bits/stdc++.h>
using namespace std;
int n;
struct treenode {int value;int l, r, fa;
} a[1000025];
int calculate(int x) {int ans = a[x].value;if (a[x].l) {ans += calculate(a[x].l); // 递归计算左子树的和}if (a[x].r) {ans += calculate(a[x].r); // 递归计算右子树的和}return ans;
}
int main() {cin >> n;for (int i = 1; i <= n; i++) {int x, y;cin >> x >> y;if (x) {a[x].fa = i;a[i].l = x;}if (y) {a[y].fa = i;a[i].r = y;}}for (int i = 1; i <= n; i++) {cin >> a[i].value;}for (int i = 1; i <= n; i++) {cout << calculate(i) << ' ';}return 0;
}
以下这种写法或许更好理解函数部分:
#include<bits/stdc++.h>
using namespace std;
int n;
struct treenode{int value;int l,r,fa;
}a[1025];
int ans;
inline void calculate(int x){ans+=a[x].value;if(a[x].l) calculate(a[x].l);if(a[x].r) calculate(a[x].r);
}
int main(){cin>>n;for(int i=1;i<=n;i++){int x,y;cin>>x>>y;if(x){a[x].fa=i;a[i].l=x; }if(y){a[y].fa=i;a[i].r=y;}}for(int i=1;i<=n;i++){cin>>a[i].value;}for(int i=1;i<=n;i++){ans=0;calculate(i);cout<<ans<<' ';}return 0;
}如果数据范围是较大的那么上述代码必定就会超时了,这时候就不能使用dfs了,考虑这么写:
#include<bits/stdc++.h>
using namespace std;
int n,cnt,v[1000001];
struct treenode{int value;int l,r,fa;
}a[1000001];
int solve(int t){int x=a[t].value;if(a[t].l) x+=solve(a[t].l);if(a[t].r) x+=solve(a[t].r);v[t]=x;return x;
}
int main(){cin>>n;for(int i=1;i<=n;i++){int x,y;cin>>x>>y;if(x){a[x].fa=i;a[i].l=x; }if(y){a[y].fa=i;a[i].r=y;}}for(int i=1;i<=n;i++){cin>>a[i].value;}solve(1);for(int i=1;i<=n;i++){cout<<v[i]<<' ';}return 0;
}这样其实主要是因为考虑到一开始在算第一个子树的左右节点,也就是根的所有子节点的权值和的时候已经把二叉树完全的遍历了一遍,所以在后续不断的递归过程中,很多都重复递归了,所以实际上只需要递归一次,然后利用了一个数组v来存储每个节点的所有子节点加上他本身的权值之和。
谢谢观看!


![[蓝桥 2023 ]三带一](https://img-blog.csdnimg.cn/img_convert/55f881eddd67977f20cb0f125da397bb.jpeg)

![[Ray Tracing: The Rest of Your Life] 笔记](https://img-blog.csdnimg.cn/direct/de08b63a43a443629f5eadf8e098a3b1.png#pic_center)