AVL树介绍以及代码实现

        二叉搜索树的查找和删除虽然最优情况下能够做到 O(logN) 的级别，但是在一些特殊情况下，它的查找速度只能到达 O(N)级别，比如数据按顺序插入，那么就一定是一棵单边树。

        为了针对这种情况，俄罗斯的两位数学家：G.M.Adelson-Velskii 和E.M.Landis在1962年 发明了一种解决上述问题的方法：当向二叉树中插入数据，需要保证树的左右高度之差的绝对值不超过1，通过这种方法能够有效的减少平均搜索长度，这种树就是AVL树。

AVL树的概念

  • 它的左右子树都是AVL树。
  • 左右子树的高度差的绝对值不超过1.

若一个二叉搜索树能够保持高度平衡，他就是AVL树，有n个节点，它的高度为 O(logN)，搜索时间为 O(logN)。

了解了AVL树的概念，就来看看它的实现代码吧。

AVL树节点的实现

template<class K,class V>
class AVLNode {
public:pair<K, V> _kv;AVLNode<K, V>* _left;AVLNode<K, V>* _right;AVLNode<K, V>* _parent;int _bf;AVLNode(pair<K, V> kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};

AVL树相比于普通的二叉搜索树，还多出了一个指向父节点的指针，以及平衡因子 _bf 。

平衡因子:本博客中的平衡因子的值等于右子树的高度-左子树的高度。

刚创建的节点的平衡因子为0.

AVL树节点的插入

bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){pNode cur = new Node(kv);_root = cur;return true;}pNode cur = _root;pNode parent = nullptr;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}//这个时候cur应该到空了，parent指向下一个cur = new Node(kv);if (parent->_kv.first > kv.first){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}while (parent){if (cur == parent->_left){parent->_bf--;}else if (cur == parent->_right){parent->_bf++;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//需要自旋if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == 1){//左右双旋RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){//右左双旋RotateRL(parent);}break;}else{assert(-1);}}
}

 AVL树的插入刚开始和二叉搜索树类似，首先找到插入节点的位置，然后再插入到该节点的位置。

不过不同的是，根据cur插入位置的不同，需要更新cur的父节点的平衡因子。

如果插入在左子树位置，父节点的平衡因子就减减，否则就加加。

而且根据父节点平衡因子的变化，有可能需要一直更新父节点的平衡因子直到根节点。

比如这样的：

假设我们插入新节点到e节点下(左右子树中任意一个)

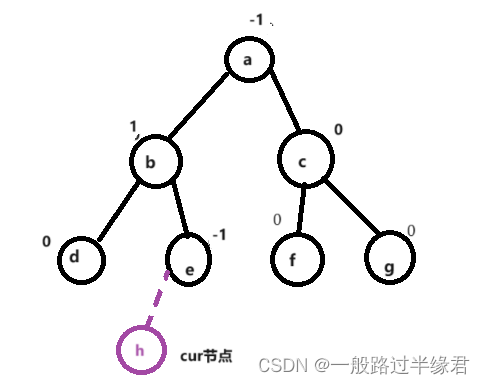
我们发现其父节点的平衡因子都需要更新，一直到根节点。

而这是有规律的。

  • 当父节点的平衡因子变为 1/-1，说明子树的高度变更，需要向上更新平衡因子
  • 当父节点的平衡因子变为0，则说明子树的高度不变，只需要更新父节点的平衡因子
  • 当父节点的平衡因子变为2/-2，则说明子树的高度过高，需要父节点自旋。 

节点的自旋

节点的共四种情况：右单旋，左单旋，左右双旋，右左双旋。

右单旋

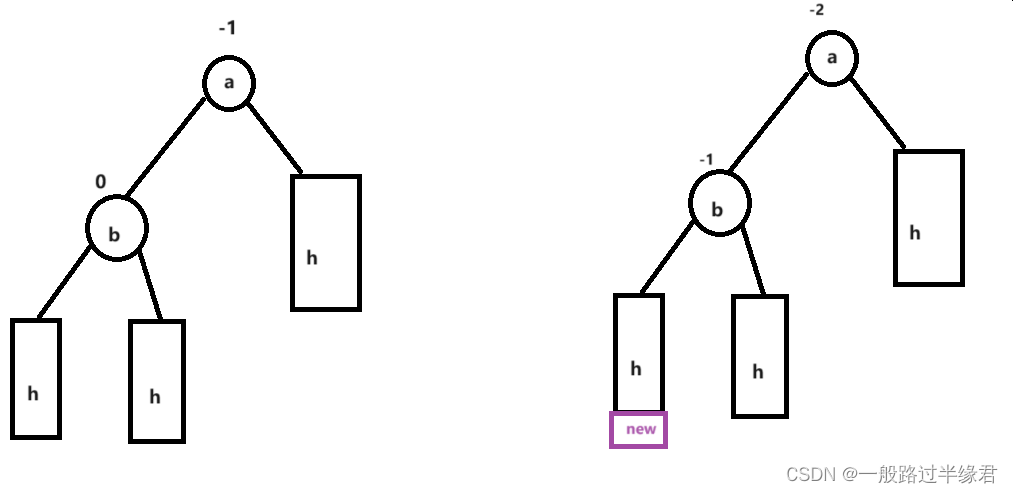 当节点插入在较高左子树的左侧时，就会出现左子树高度-右子树高度 = -2，导致左右不平衡，此时需要使平衡因子=-2的节点进行左旋，变成下面的样子。

  • 将a节点连接到b节点的右指针（a肯定大于b节点）
  • 将b节点的右子树连接到a节点的左指针（b的右子树肯定都小于a）
  • 再更新平衡因子

我们发现通过右单旋，a节点和b节点的平衡因子都变为0了。

通过这个思路，可以得到代码。

void RotateR(pNode parent)
{pNode pleft = parent->_left;pNode pleft_R = pleft->_right;pNode P_parent = parent->_parent;//将左子树的右指针指向parentpleft->_right = parent;//将parnet 的左指针指向左子树的右节点parent->_left = pleft_R;if (pleft_R){//若左子树的右节点不为空，就将它的父节点设置为parentpleft_R->_parent = parent;}//将左子树设置为parent的父节点parent->_parent = pleft;pleft->_parent = P_parent;if (P_parent == nullptr){_root = pleft;pleft->_parent = nullptr;}else{if (parent == P_parent->_left){P_parent->_left = pleft;}else if (parent == P_parent->_right){P_parent->_right = pleft;}}parent->_bf = pleft->_bf = 0;
}

左单旋

当节点插入在较高右子树的右节点，就需要进行左单旋。

左单旋的过程和右单旋一样，只是方向是不同的。

  • 将a节点连接到b节点的左指针（a肯定小于b节点）
  • 将b节点的左子树连接到a节点的右指针（b的左子树肯定都大于a）
  • 再更新平衡因子
	void RotateL(pNode parent){pNode pright = parent->_right;pNode pright_L = pright->_left;pNode P_parent = parent->_parent;//将右子树的左指针指向parentpright->_left = parent;//将parnet 的右指针指向左子树的右节点parent->_right = pright_L;if (pright_L){//若左子树的右节点不为空，就将它的父节点设置为parentpright_L->_parent = parent;}//将左子树设置为parent的父节点parent->_parent = pright;pright->_parent = P_parent;if (P_parent == nullptr){_root = pright;pright->_parent = nullptr;}else{if (parent == P_parent->_left){P_parent->_left = pright;}else if (parent == P_parent->_right){P_parent->_right = pright;}}parent->_bf = pright->_bf = 0;}

左右双旋

这种情况可以看做右单旋的另一种节点插入情况。

右单旋是插入较高左子树的左侧，而当新节点插入较高左子树的右侧时就会出现新的情况。

此处新节点可以插在c节点的左子树或者右子树，都一样，只是最后平衡因子更新不同。 

这种情况下无论是单纯的左单旋还是右单旋都没有用，需要两个一起来。

  • 先以b节点作为父节点来进行一次左单旋。
  • 然后再以a节点作为父节点来进行一次右单旋。
  • 最后查看新节点是在c节点的左子树还是右子树来进行平衡节点的更新。

通过左右双旋能够使AVL树平衡，不过根据新节点的位置，a和b的平衡因子会不同。

比如新节点在c节点的左子树上，那么b的平衡因子为0，a的平衡因子为1。

新节点在c节点的右子树上，b的平衡因子为-1，a的平衡因子为0。

void RotateLR(pNode parent)
{pNode subL = parent->_left;pNode subLR = subL->_right;int bf = subLR->_bf;RotateL(subL);RotateR(parent);if (bf == 1)//新增节点在右边{subL->_bf = -1;parent->_bf = 0;subLR->_bf = 0;}else if (bf == -1)//新增节点在左边{subL->_bf = 0;parent->_bf = 1;subLR->_bf = 0;}else if (bf == 0)//本身是新增节点{subL->_bf = 0;parent->_bf = 0;subLR->_bf = 0;}else{assert(false);}
}

右左双旋

右左双旋就是左旋的另一种情况：新节点在较高右子树的左节点，情况和左右双旋一样，需要两个单旋合作来实现平衡。

void RotateRL(pNode parent)
{pNode subR = parent->_right;pNode subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);if (bf == 1)//新增节点在右边{subR->_bf = 0;parent->_bf = -1;subRL->_bf = 0;}else if (bf == -1)//新增节点在左边{subR->_bf = 1;parent->_bf = 0;subRL->_bf = 0;}else if (bf == 0)//本身是新增节点{subR->_bf = 0;parent->_bf = 0;subRL->_bf = 0;}else{assert(false);}
}

通过这四种方式能够保证AVL树的平衡。

AVL树的验证

验证AVL树是否是AVL树，有两个条件：

  • 左右子树的高度差是否等于平衡因子
  • 节点的左右子树都是AVL树

因此我们通过递归来检查AVL树是否是AVL树。

	bool IsBalance(){return _IsBalance(_root);}bool _IsBalance(pNode root){if (root == nullptr){return true;}int left = Height(root->_left);int right = Height(root->_right);int dff = right - left;if (dff != root->_bf){cout << "平衡因子异常" << endl;return false;}return abs(dff) != 2 && _IsBalance(root->_left) && _IsBalance(root->_right);}int Height(pNode root){if (root == nullptr){return 0;}int left = Height(root->_left);int right = Height(root->_right);return left > right ? left + 1 : right + 1;}

通过递归遍历检查，可以检查是否是AVL树。

AVL树的删除

AVL树的删除大致和二叉搜索树类似，不过不同的是，AVL树需要更新平衡因子，当删除节点后，有节点的平衡因子变为-2/2时，就需要进行自旋。

平衡因子的更新

删除节点时的平衡因子的更新和插入节点时平衡因子的更新正好相反。

  • 当左节点被删除时，父节点的平衡因子需要++
  • 当右节点被删除时，父节点的平衡因子需要--
  • 当父节点的平衡因子变为1/-1时，说明原本的平衡因子为0，删除后节点的高度不变，不用向上更新节点
  • 当父节点的平衡因子变为0时，说明原本的平衡因子为1/-1，删除后节点的高度变化，需要向上更新节点
  • 当父节点的平衡因子变为2/-2时，说明高度过高，需要自旋
父节点的平衡因子为-2时

这种情况下有三种情况：父节点的左子树的平衡因子为 0/1/-1。

左子树平衡因子为0时

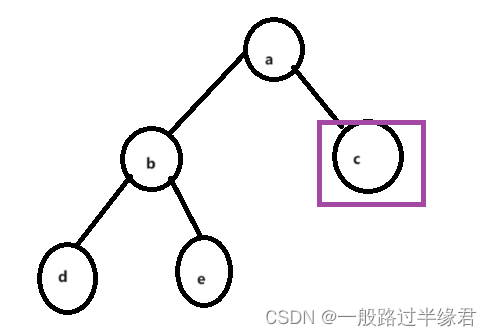
 如图，删除c节点后，a节点的平衡因子变为-2，而b的平衡因子为0。

这种情况我们可以直接看做是插入的右单旋或者左右单旋的情况，此处我们可以直接用右单旋。

左子树平衡因子为1时

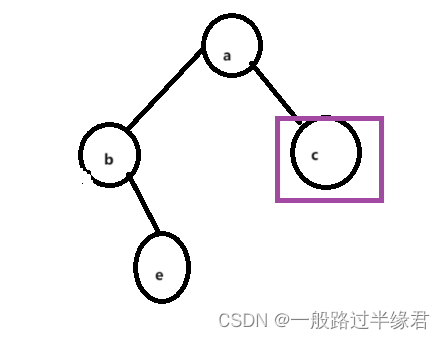
这种情况下就是左右双旋的情况，需要先对b节点进行左单旋，再对a节点进行右单旋。

左子树的平衡因子为-1时

这种情况下就是单纯的右单旋了。 

父节点的平衡因子为2时

右子树的平衡因子为0时

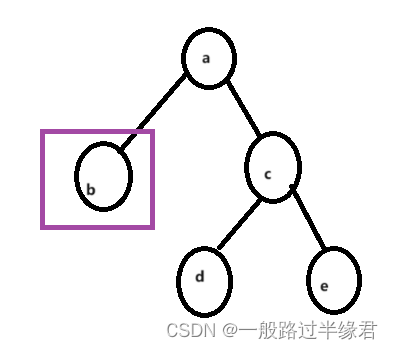
这种情况下可以单纯采用左单旋

右子树的平衡因子为-1时

这种情况下需要采用右左单旋

 平衡因子为1时

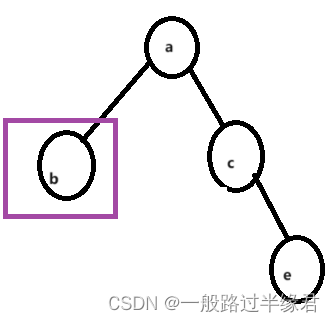
这种情况下就可以直接采用左单旋。 

删除的更新代码
void DelUpdate(pNode cur, pNode parent)
{while (parent){//删除左节点就需要++if (cur == parent->_left){parent->_bf++;}else if (cur == parent->_right){parent->_bf--;}if (parent->_bf == 0){cur = parent;parent = parent->_parent;}else if (parent->_bf == 1 || parent->_bf == -1){break;}else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == 2){if (parent->_right->_bf == 0){pNode p_right = parent->_right;RotateL(parent);parent->_bf = 1;p_right->_bf = -1;break;}else if (parent->_right->_bf == 1){RotateL(parent);}else if (parent->_right->_bf == -1){RotateRL(parent);}cur = parent;parent = parent->_parent;}else if (parent->_bf == -2){if (parent->_left->_bf == 0){pNode p_left = parent->_left;RotateR(parent);parent->_bf = -1;p_left->_bf = 1;break;}else if(parent->_bf == 1){RotateLR(parent);}else if (parent->_left->_bf == -1){RotateL(parent);}cur = parent;parent = parent->_parent;}}}
}

删除时的更新并未直接删除节点，删除节点的操作应该在平衡因子更新后再进行操作。

节点的删除

节点的删除有三种情况：左右为空，有一边不为空，左右都不为空。

左右为空

当节点的左右都为空时，就在更新平衡因子后直接删除该节点，然后根据节点的位置来使父节点的指针指向空。

如图，删除的d节点是b节点的左节点，那么需要使b节点的左节点指向空。 

右一边不为空

这个时候还需要把d节点连接到a节点的左指针，把d节点的父指针指向a节点后再删除b节点。

左一边不为空

 这个时候需要把d节点连接到a节点的左指针上，再更新d节点的父指针。

左右不为空

这个情况下，我们需要找到cur（被删除节点）的右子树中的最小节点，也就是右子树的最左节点，然后交换最左节点和cur的值，再删除最左节点即可。

注意：minright是最左节点，但不一定没有右子树，因此需要检查是否有右子树，将右子树连接到minright的父节点的左指针上。 

代码实现
bool Erase(const pair<K, V>& kv)
{pNode cur = Find(kv);pNode parent = cur->_parent;pNode delnode = cur;if (cur == nullptr){return false;}//若左右都是空树else if (cur->_left == nullptr && cur->_right == nullptr){//若是根还需要将_root 置空if (_root == cur){_root = nullptr;delete cur;}//若不是根还需要向上调整else{//更新后cur和parent都会改变，因此需要重新赋值DelUpdate(cur, parent);parent = delnode->_parent;if (delnode == parent->_left){parent->_left = nullptr;}else{parent->_right = nullptr;}delete delnode;}}else if (cur->_left == nullptr && cur->_right != nullptr){//左为空右不为空if (cur == _root){//若是根节点_root = cur->_right;_root->_parent = nullptr;delete cur;}else{pNode delnode = cur;//更新平衡因子DelUpdate(cur, parent);parent = delnode->_parent;pNode cur_R = delnode->_right;cur_R->_parent = parent;if (delnode == parent->_left){parent->_left = cur_R;}else if (delnode == parent->_right){parent->_right = cur_R;}delete delnode;}}else if (cur->_left != nullptr && cur->_right == nullptr){if (cur == _root){//若是根节点_root = cur->_left;_root->_parent = nullptr;delete cur;}else{pNode delnode = cur;//更新平衡因子DelUpdate(cur, parent);parent = delnode->_parent;pNode cur_L = delnode->_left;cur_L->_parent = parent;if (delnode == parent->_left){parent->_left = cur_L;}else if (delnode == parent->_right){parent->_right = cur_L;}delete delnode;}}//左右都不空else{pNode minRight = cur->_right;pNode minRight_P = cur;//找到右子树的最左节点while (minRight->_left){minRight_P = minRight;minRight = minRight->_left;}//交换它们的值cur->_kv.first = minRight->_kv.first;cur->_kv.second = minRight->_kv.second;//记录下最左节点的右子树,由于更新平衡因子会改变minRight的指向，因此记录下minRightpNode minRight_R = minRight->_right;pNode tmp = minRight;//更新平衡因子DelUpdate(minRight, minRight_P);minRight = tmp;minRight_P = minRight->_parent;if (minRight == minRight_P->_left){if (minRight_R != nullptr){minRight_R->_parent = minRight_P;}minRight_P->_left = minRight_R;}else if (minRight == minRight_P->_right){if (minRight_R != nullptr){minRight_R->_parent = minRight_P;}minRight_P->_right = minRight_R;}delete minRight;}return true;
}

 总结

        这就是AVL树的总结和实现了，作为map和set的底层结构，AVL树的结构十分重要，需要各位同学好好学习。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/232624.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

字节跳动基础架构SRE-Copilot获得2023 CCF国际AIOps挑战赛冠军

字节跳动基础架构SRE-Copilot获得2023 CCF国际AIOps挑战赛冠军

近日&#xff0c;2023 CCF国际AIOps挑战赛决赛暨“大模型时代的AIOps”研讨会在北京成功举办&#xff0c;活动吸引了来自互联网、运营商、科研院所、高校、软硬件厂商等领域多名专家学者参与&#xff0c;为智能运维的前沿学术研究、落地生产实践打开了新思路。决赛中&#xff0…
阅读更多...
安全加密基础—基本概念、keytool、openssl

安全加密基础—基本概念、keytool、openssl

安全加密基础—基本概念、keytool、openssl 目录 前言 一、概念 明文通信 无密钥密文通信 对称加密 非对称加密 数字签名 消息摘要(MD5) CA数字证书(解决公钥分发的问题) HTTPS 相关文件扩展名 常用后缀名 普通的pem文件内容 二、keytool 2.1常用的命令如下 2…
阅读更多...
【linux踩雷】Ubuntu中su root密码无法使用

【linux踩雷】Ubuntu中su root密码无法使用

【linux踩雷】Ubuntu中su root密码无法使用 在ubuntu的安装过程中&#xff0c;没有出现设置root密码&#xff0c;以为密码为空&#xff0c;但是却不能使用 解决方法&#xff1a; 先用sudo passwd更改密码&#xff0c;再去su root就可以了。
阅读更多...
2024前端炫酷源码分享（附效果图及在线演示）

2024前端炫酷源码分享（附效果图及在线演示）

分享10款非常有趣的前端特效源码 其中包含css动画特效、js原生特效、svg特效以及小游戏等 下面我会给出特效样式图或演示效果图 但你也可以点击在线预览查看源码的最终展示效果及下载源码资源 GSAP-火箭动画特效 GSAP 火箭动画 当氮气充足的情况下 火箭会冲出 并继续飞行 图片…
阅读更多...
AI教我学编程之C#关键字

AI教我学编程之C#关键字

AI教我学编程系列学习第三课 — C#关键字 前言重点先知关键字分类保留字上下文关键字 对话AI首遇波澜调整指令第一次第二次第三次直到我提出如下指令 人工智能&#xff1f;阶段总结 知识拓展1、Ecma和ISO是什么&#xff1f;2、System&#xff0c;dllhost.exe&#xff0c;taskmg…
阅读更多...
推荐几个免费的HTTP接口Mock网站和工具

推荐几个免费的HTTP接口Mock网站和工具

在前后端分离开发架构下&#xff0c;经常遇到调用后端数据API接口进行测试、集成、联调等需求&#xff0c;比如&#xff1a; &#xff08;1&#xff09;前端开发人员很快开发完成了UI界面&#xff0c;但后端开发人员的API接口还没有完成&#xff0c;不能进行前后端数据接口对接…
阅读更多...
html5实现好看的个人博客模板源码

html5实现好看的个人博客模板源码

文章目录 1.设计来源1.1 主界面1.2 认识我界面1.3 我的文章界面1.4 我的模板界面1.5 文章内容界面 2.结构和源码2.1 目录结构2.2 源代码 源码下载 作者&#xff1a;xcLeigh 文章地址&#xff1a;https://blog.csdn.net/weixin_43151418/article/details/135368653 html5实现好看…
阅读更多...
【数据库原理】（11）SQL数据查询功能

【数据库原理】（11）SQL数据查询功能

基本格式 SELECT [ALL|DISTINCT]<目标列表达式>[,目标列表达式>]... FROM <表名或视图名>[,<表名或视图名>] ... [ WHERE <条件表达式>] [GROUP BY<列名 1>[HAVING <条件表达式>]] [ORDER BY <列名 2>[ASC DESC]];SELECT: 指定要…
阅读更多...
网络知识-以太网技术的发展及网络设备

网络知识-以太网技术的发展及网络设备

目 录 一、背景介绍 &#xff08;一&#xff09;网络技术的时代 &#xff08;二&#xff09;以太网技术脱颖而出 二、以太网的工作原理 &#xff08;一&#xff09;、载波侦听多路访问&#xff08;CSMA/CD&#xff09; 1、数据发送流程 2、发送过程解析 3、…
阅读更多...
CAN协议

CAN协议

文章目录 CAN介绍CAN的优势多主控制通信速度较快&#xff0c;通信距离远具有错误检测、错误通知和错误恢复功能故障封闭功能连接节点多 ISO11519-2物理层特性ISO11898物理层特性CAN 收发芯片 JTA1050 CAN 协议5 种帧5种帧介绍数据帧的构成帧起始仲裁段控制段数据段CRC段ACK段帧…
阅读更多...
应用OpenCV绘制箭头

应用OpenCV绘制箭头

绘制箭头函数 方法&#xff1a;函数cv2.arrowedLine( ) 语法格式&#xff1a;cv2.arrowedLine(img, pt1, pt2, color[, thickness[, line_type[, shift[, tipLength]]]]) 参数说明&#xff1a; img&#xff1a;要画的直线所在的图像&#xff0c;也称为画布。。 pt1&#x…
阅读更多...
ubuntu 22 virt-manger(kvm)安装winxp； ubuntu22体验 firebird3.0

ubuntu 22 virt-manger(kvm)安装winxp； ubuntu22体验 firebird3.0

安装 、启动 virt-manager sudo apt install virt-manager sudo systemctl start libvirtdsudo virt-manager安装windowsXP 安装过程截图如下 要点1 启用 “包括寿终正寝的操作系统” win_xp.iso 安装过程 &#xff1a; 从winXp.iso启动, 执行完自己重启从硬盘重启&#xff0c…
阅读更多...
【已解决】Invalid bound statement (not found)

【已解决】Invalid bound statement (not found)

报错讯息 org.apache.ibatis.binding.BindingException: Invalid bound statement (not found): com.casey.mapper.SysRoleMapper.getUserRoleCode at org.apache.ibatis.binding.MapperMethod S q l C o m m a n d . < i n i t > ( M a p p e r M e t h o d . j a v a :…
阅读更多...
基于java,springboot的论旅游管理系统设计与实现

基于java,springboot的论旅游管理系统设计与实现

环境以及简介 基于java,springboot的论旅游管理系统设计与实现&#xff0c;Java项目&#xff0c;SpringBoot项目&#xff0c;含开发文档&#xff0c;源码&#xff0c;数据库以及ppt 源码下载 环境配置&#xff1a; 框架&#xff1a;springboot JDK版本&#xff1a;JDK1.8 服…
阅读更多...
关于“Python”的核心知识点整理大全65

关于“Python”的核心知识点整理大全65

目录 20.2.19 设置 SECRET_KEY 20.2.20 将项目从 Heroku 删除 注意 20.3 小结 附录 A 安装Python A.1.1 确定已安装的版本 A.1.2 在 Linux 系统中安装 Python 3 A.2 在 OS X 系统中安装 Python A.2.1 确定已安装的版本 A.2.2 使用 Homebrew 来安装 Python 3 注意 …
阅读更多...
[C#]使用DlibDotNet人脸检测人脸68特征点识别人脸5特征点识别人脸对齐人脸比对FaceMesh

[C#]使用DlibDotNet人脸检测人脸68特征点识别人脸5特征点识别人脸对齐人脸比对FaceMesh

【官方框架地址】 https://github.com/takuya-takeuchi/DlibDotNet 【算法介绍】 DlibDotNet是一个开源的.NET库&#xff0c;用于实现机器学习和计算机视觉应用。它基于C库dlib&#xff0c;通过C/CLI封装了dlib的所有功能&#xff0c;为.NET开发者提供了简单易用的API。以下是…
阅读更多...
缘分的计算

缘分的计算

题目描述&#xff1a; 缘分是一个外国人难以理解的中文名词。大致说来&#xff0c;缘分是一种冥冥中将两人&#xff08;通常是情人&#xff09;结合的力量。仅管这是种迷信&#xff0c;很多人——特别是女生——喜欢去计算它。 不幸的是&#xff0c;644 也是这样。有天&#x…
阅读更多...
Oracle-深入了解cache buffer chain

Oracle-深入了解cache buffer chain

文章目录 1.Cache buffer chain介绍2.Buffer cache的工作原理3 Buffer chains4.Multi-versioning of Buffers5.Latches6.诊断CBC latch等待7.解决 CBC Latch等待 1.Cache buffer chain介绍 经常看到会话等待事件“latch&#xff1a;cache buffers chain”。 如果想知道意味着什…
阅读更多...
vue3 + TS + vite 搭建中后台管理系统（完整项目）

vue3 + TS + vite 搭建中后台管理系统（完整项目）

vue3 TS vite 搭建中后台管理系统&#xff08;完整项目&#xff09; 前言1、搭建步骤及方法2、集成多种插件功能&#xff0c;实现中后台按需使用3、新手学TS如何快速进入状态、定义TS类型4、layout搭建四款常见风格6、大屏搭建效果5、vue3Ts运营管理系统总结&#xff1a; 前言…
阅读更多...
力扣hot100 将有序数组转换为二叉搜索树 递归

力扣hot100 将有序数组转换为二叉搜索树 递归

&#x1f468;‍&#x1f3eb; 题目地址 时间复杂度&#xff1a; O ( n ) O(n) O(n) &#x1f60b; AC code /*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNod…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023