【数据结构】二叉树的创建和遍历：前序遍历，中序遍历，后序遍历，层次遍历

一、二叉树的定义

1、二叉树的定义

2、二叉树的五种形态

二叉树的子树：

3、满二叉树与完全二叉树

4、二叉树的性质

5、二叉树的存储结构

1、顺序存储

编辑

2、链式存储

二、二叉树的遍历

按照前序序列构建二叉树

1、前 (先) 序遍历(Preorder Traversal )

前序遍历动态过程图：

下面是前序遍历的递归图解：

前序遍历代码及注释：

2. 中序遍历(Inorder Traversal)

中序遍历动态过程图：

中序遍历代码及注释：

3. 后序遍历(Postorder Traversal)

后序遍历动态过程图：

后序遍历代码及注释：

4、层序遍历

层序遍历代码及注释：

一、二叉树的定义

1、二叉树的定义

二叉树（Binary Tree）是有n（n≥0）个结点的有限集合：
（1) 该集合或者为空（n=0)；
（2）或者由一个根结点及两个不相交的分别称为左子树和右子树组成的非空树；
（3）左子树和右子树同样又都是二叉树。
在一棵非空的二叉树中，每个结点至多只有两棵子树，分别称为左子树和右子树，且左右子树的次序不能任意交换。所以，二叉树是特殊的有序树。值得注意的是，由于二叉树上任结点的子树有左、右之分，因此即使一个结点只有一棵非空子树，仍须区别它是该结点的左子树还是右子树，这是与树不同的。

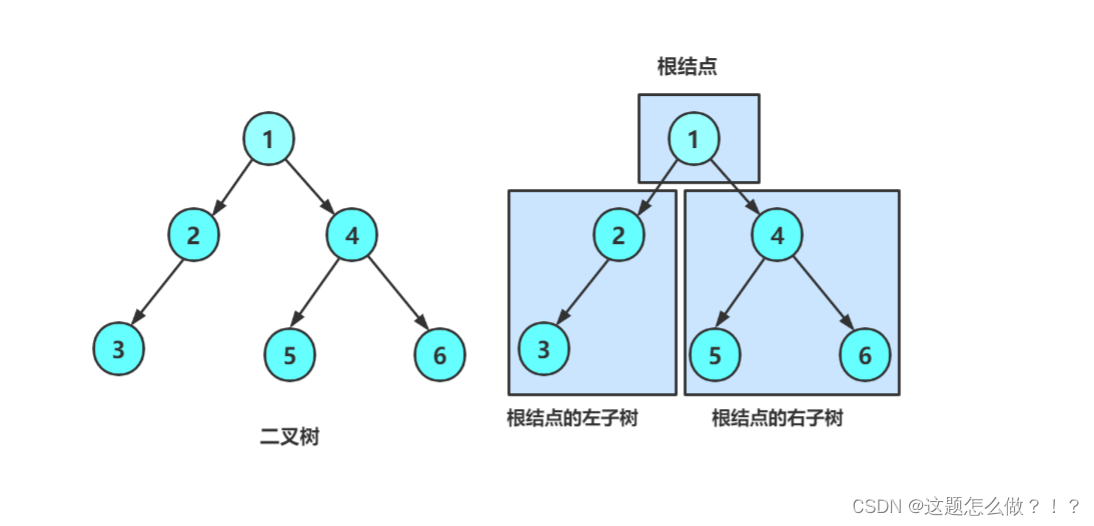
2、二叉树的五种形态

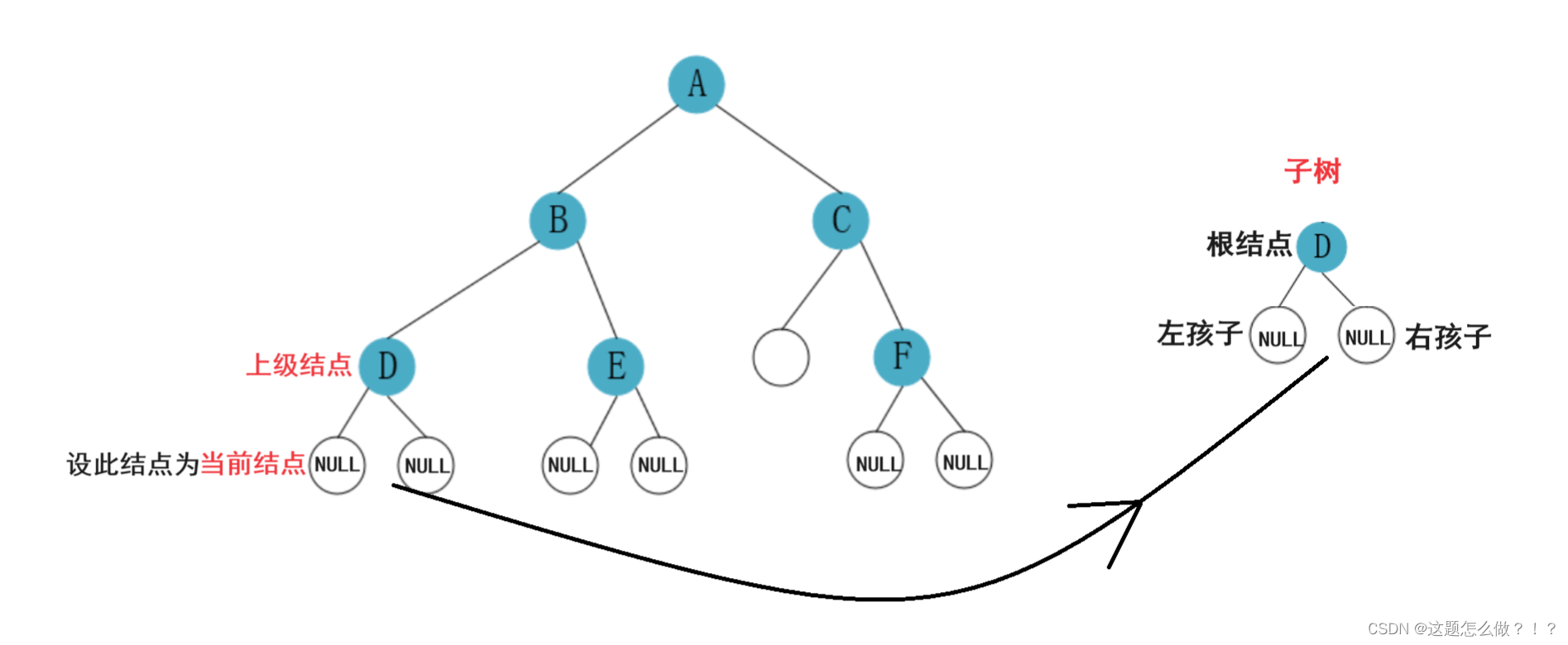
二叉树的子树：

在二叉树中，一个子树是指由二叉树中的某个节点及其后代节点组成的树。换句话说，对于一个给定的二叉树，可以选择其中的一个节点作为子树的根节点，并且包含该节点的所有后代节点，形成一个新的子树。

具体定义如下：
在一个二叉树中，每个节点最多只有两个子节点，分别为左子节点和右子节点。对于任意一个节点，在它的左子节点和右子节点上又可以分别构成两个独立的子树，这样就形成了一个递归的结构。

3、满二叉树与完全二叉树

1. 满二叉树：一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是，则它就是满二叉树。
2. 完全二叉树：完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。特点：树高为h时，前h-1层节点为满。 要注意的是满二叉树是一种特殊的完全二叉树。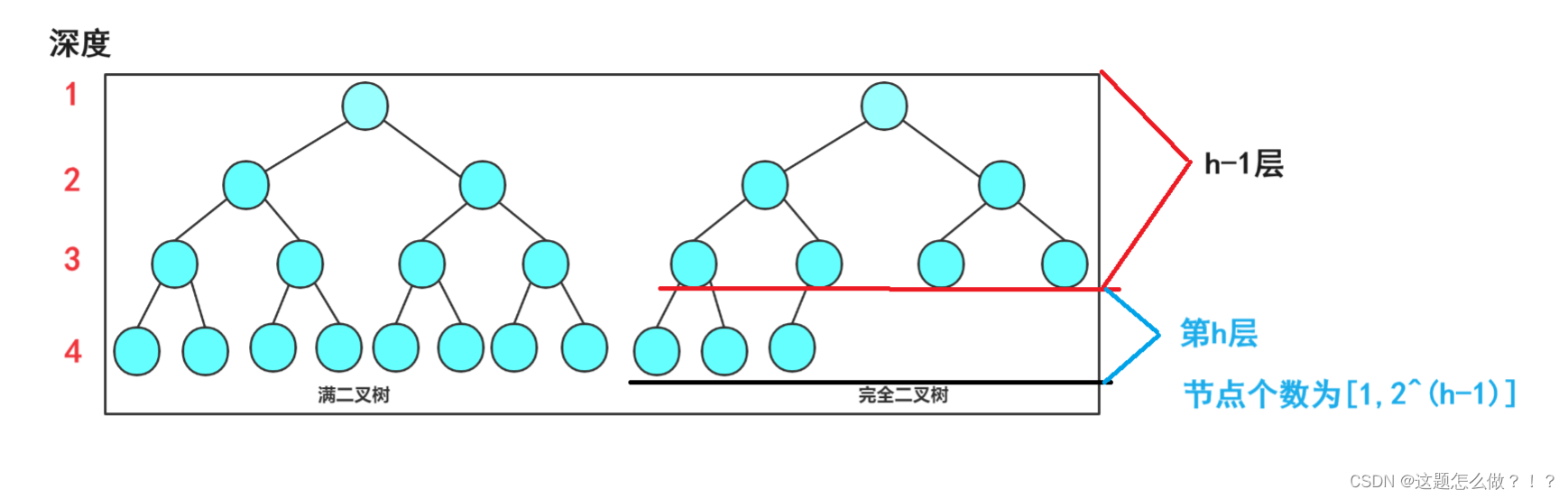

4、二叉树的性质

若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有2^(i-1)个结点。
若规定根节点的层数为1，则深度为h的二叉树的最大结点数是2^h-1。
对任何一棵二叉树, 如果度为0的叶结点个数为n0，度为2的分支结点个数为n2，则有 n0 = n2 + 1。
若规定根节点的层数为1，具有n个结点的满二叉树的深度h= log2(n+1)。（这里的log是以2为底的对数）
对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，则对于序号为i的结点有：
a. 若i > 0，i位置节点的双亲序号为(i-1)/2，若i = 0，则i为根节点编号，无双亲节点。
b. 若2i+1 < n，左孩子序号为2i+1，若2i+1 >= n，则无左孩子。
c. 若2i+2 < n，右孩子序号为2i+2，若2i+2 >= n，则无右孩子。

5、二叉树的存储结构

二叉树一般可以使用两种结构存储，一种顺序结构，一种链式结构。

1、顺序存储

顺序结构存储就是使用数组来存储，一般使用数组只适合表示完全二叉树，因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储，关于堆我们后面的博客会专门讲解。二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树。

2、链式存储

二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址。链式结构又分为二叉链和三叉链，本节内容我们主要讲解二叉链式存储结构。

链式二叉树结点定义如下：

typedef char BTDataType; // 使用typedef关键字给char类型取了一个别名BTDataTypetypedef struct BTNode // 使用struct关键字定义了一个名为BTNode的结构体
{BTDataType data;        // 二叉树节点的数据域，用于存储具体的数据值struct BTNode* left;    // 二叉树节点的左子节点指针，指向左子节点struct BTNode* right;   // 二叉树节点的右子节点指针，指向右子节点
} BTNode;   // 使用BTNode作为该结构体类型的别名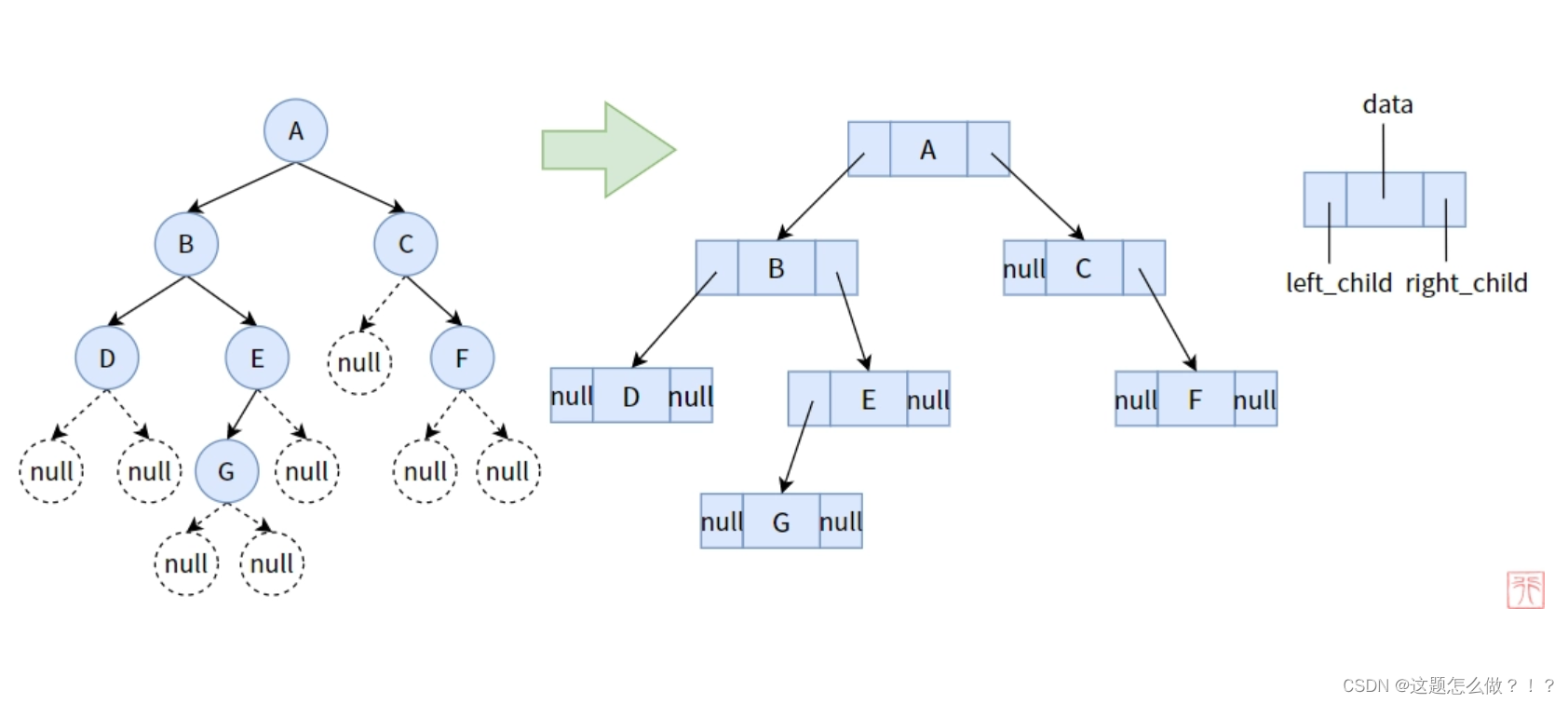

二、二叉树的遍历

按照前序序列构建二叉树

在对二叉树进行遍历之前我们先对通过前序遍历的数组"ABD##E#H##CF##G##"构建一颗二叉树。注意：'#' 字符代表该节点为空。

// 前序建立二叉树的函数
BTNode* CreateBinaryTreePre(BTDataType* a, int n, int* pi)
{// 如果数组索引超出数组长度，返回空指针if (*pi >= n){return NULL;}// 如果当前位置的值为 '#'，表示当前位置为空节点，将数组索引向后移动，并返回空指针if (a[*pi] == '#'){(*pi)++;return NULL;}// 动态分配一个新的二叉树节点BTNode* root = (BTNode*)malloc(sizeof(BTNode));// 如果内存分配成功if (root){// 将当前位置的值存储到新节点的数据域中root->data = a[(*pi)++];// 递归调用CreateBinaryTreePre函数，构建新节点的左子树root->left = CreateBinaryTreePre(a, n, pi);// 递归调用CreateBinaryTreePre函数，构建新节点的右子树root->right = CreateBinaryTreePre(a, n, pi);}else{// 如果内存分配失败，打印错误信息并退出程序perror("malloc fail!");exit(-1);}return root;  // 返回根节点
}// 主函数
int main()
{BTNode* root;   // 定义二叉树的根节点指针BTDataType a[] = { 'A','B','D','#','#','E','#','H','#','#','C','F','#','#','G','#','#' ,'\0' };int n = strlen(a);int pi = 0;   // 定义一个变量用于追踪数组的索引位置// 调用CreateBinaryTreePre函数，传入数组a、数组长度n和索引位置的指针pi，//生成二叉树，并返回根节点指针root = CreateBinaryTreePre(a, n, &pi);return 0;
}

1、前 (先) 序遍历(Preorder Traversal )

访问根结点的操作发生在遍历其左右子树之前——即： 根节点 -> 左子树 -> 右子树。

前序遍历二叉树的算法可以按照如下的步骤实现：

如果二叉树为空，直接返回。
访问当前节点，即输出当前节点的值。
对当前节点的左子树进行前序遍历。
对当前节点的右子树进行前序遍历。

我们如何理解遍历顺序呢？博主在这里分享一下自己的方法：

对于一棵二叉树，我们先找到其根节点，打印出根结点的值后，我们对其左子树进行遍历。由于一颗二叉树可以划分出许多子树，那么遍历左子树时我们即可将当前节点（即根结点的左孩子结点）看作左子树的根结点，然后对当前子树再进行根节点 -> 左子树 -> 右子树 的遍历方法，如果当前结点为空，返回上一层递归。在当前根节点的左子树遍历完成时我们再对右子树进行遍历，如此循环往复，直至遍历完整棵树停止。

简而言之，就是当遍历到一个新结点时，把当前结点当作根节点，接着去遍历当前结点的左右子树。进入下一个子树遍历时，继续把当前结点当作根节点，如此循环往复下去，直至遇到空结点，递归开始回溯。

前序遍历动态过程图：

下面是前序遍历的递归图解：

前序遍历代码及注释：

// 前序遍历二叉树
void PrintPreOrder(BTNode* root)
{// 如果当前节点为空，返回if (!root){return;}// 打印当前节点的值printf("%c ", root->data);// 递归遍历左子树PrintPreOrder(root->left);// 递归遍历右子树PrintPreOrder(root->right);
}

2. 中序遍历(Inorder Traversal)

访问根结点的操作发生在遍历其左右子树之中（间）——即： 左子树 --> 根节点 --> 右子树。

中序遍历二叉树的算法可以按照如下步骤实现：

如果二叉树为空，直接返回。
对当前节点的左子树进行中序遍历。
访问当前节点，即输出当前节点的值。
对当前节点的右子树进行中序遍历。

对于中序遍历，我们采取类似的方法。当我们遍历时，将当前结点当作子树的根节点，先去寻找该根节点有没有左孩子，如果有，我们就向左进行遍历，当到达新结点时，我们依旧将其看作根节点去寻找该结点的左孩子，如果当前结点为空，再回溯到其父结点打印数据，再去寻找它的右孩子。当当前子树遍历完成时，我们回溯到此子树根节点的上一层的节点，打印节点数据，之后再去找该结点的右孩子。如此循环往复，直至遍历完整棵树停止。

中序遍历动态过程图：

中序遍历代码及注释：

// 中序遍历
void PrintInOrder(BTNode* root)
{// 如果当前节点为空，即已经到达叶子节点或者是空树的情况，直接返回if (!root){return;}// 递归调用中序遍历函数，遍历左子树PrintInOrder(root->left);// 打印当前节点的数据printf("%c ", root->data);// 递归调用中序遍历函数，遍历右子树PrintInOrder(root->right);
}

3. 后序遍历(Postorder Traversal)

访问根结点的操作发生在遍历其左右子树之后——即： 左子树 -->右子树 --> 根节点。

后序遍历二叉树的算法可以按照如下的步骤实现：

如果二叉树为空，直接返回。
对当前节点的左子树进行后序遍历。
对当前节点的右子树进行后序遍历。
访问当前节点，即输出当前节点的值。

对于后序遍历，我们依然按照之前的方法。当我们遍历时，将当前结点当作子树的根节点，先去寻找该根节点有没有左孩子，如果有，我们就向左进行遍历，直至树的底部；如果当前结点为空，返回上一层递归，再去判断当前节点有没有右孩子，如果有我们再向右遍历，重复上面的过程。当当前子树左右孩子遍历完后，我们回退至子树的根结点打印数据。如此循环往复，直至遍历完整棵树停止。

后序遍历动态过程图：

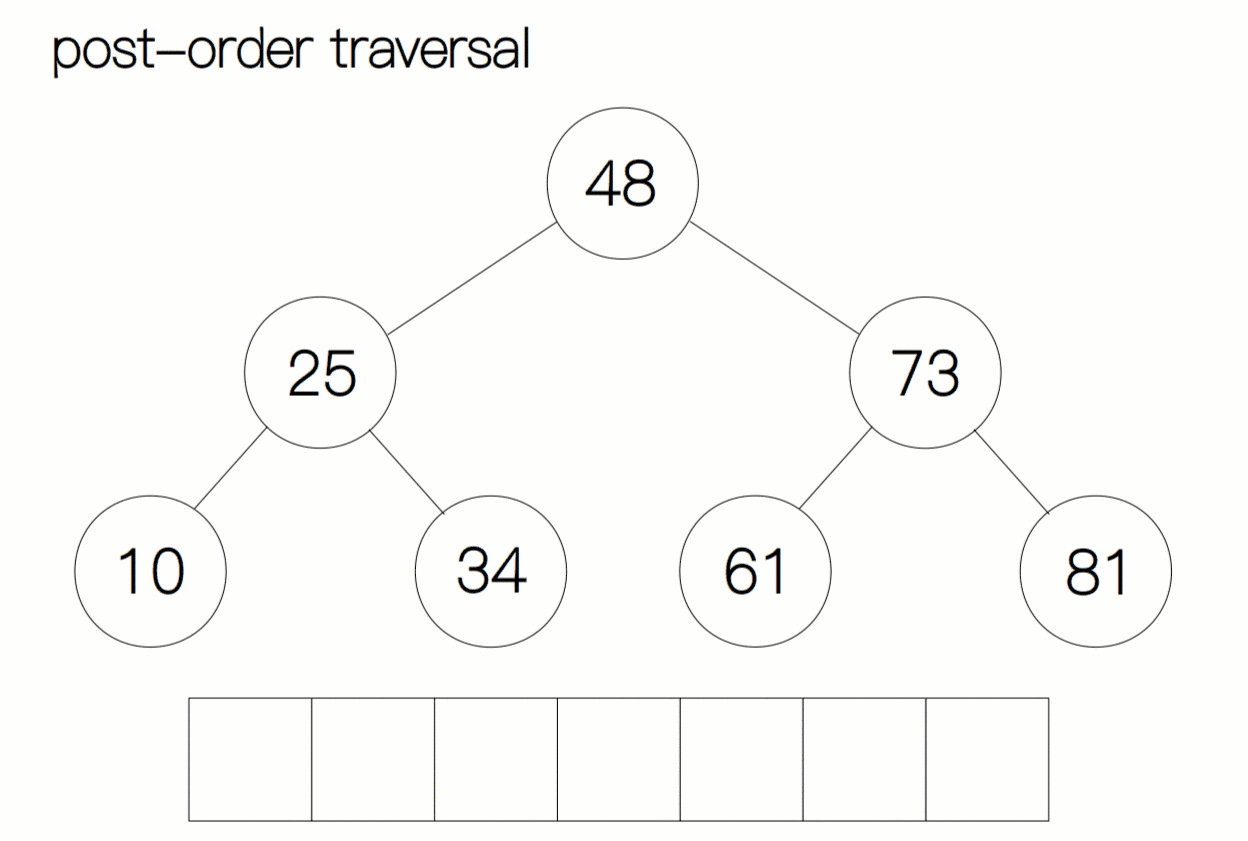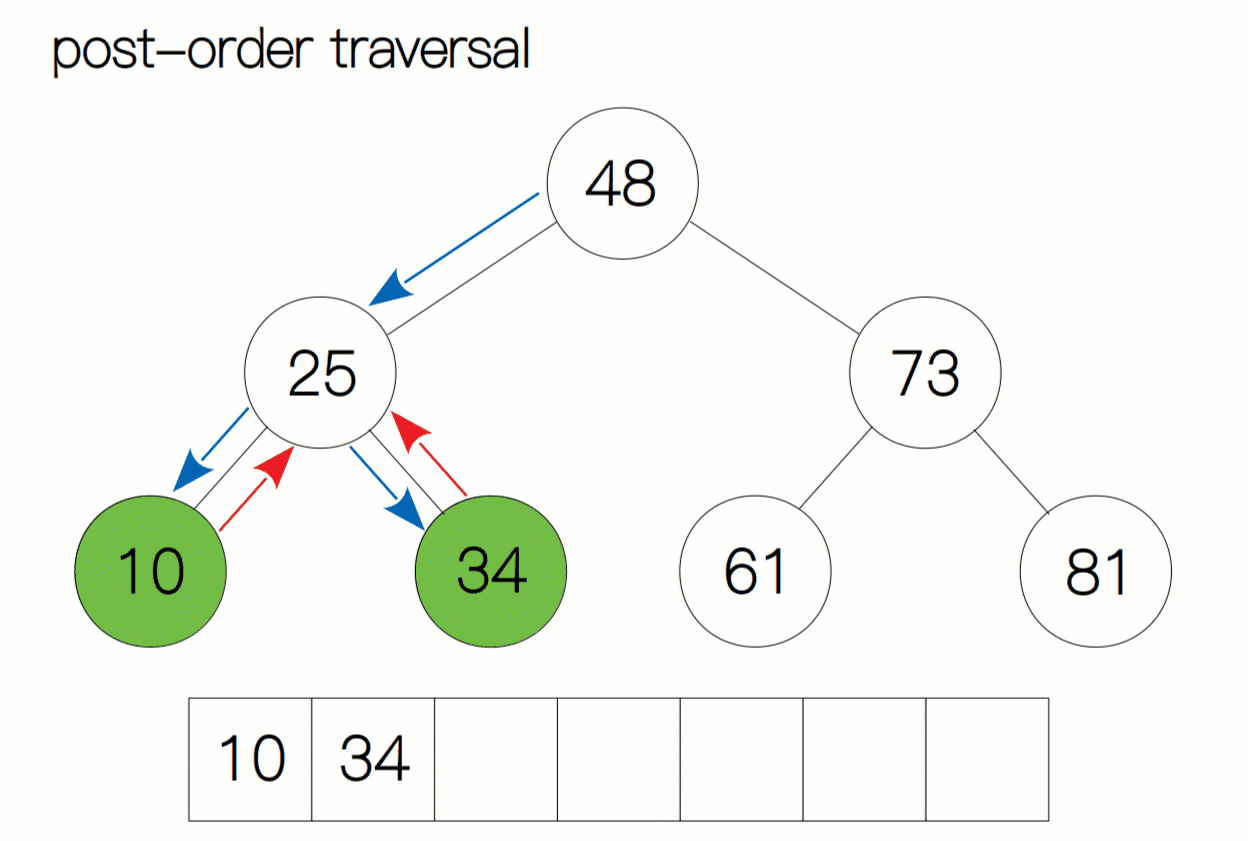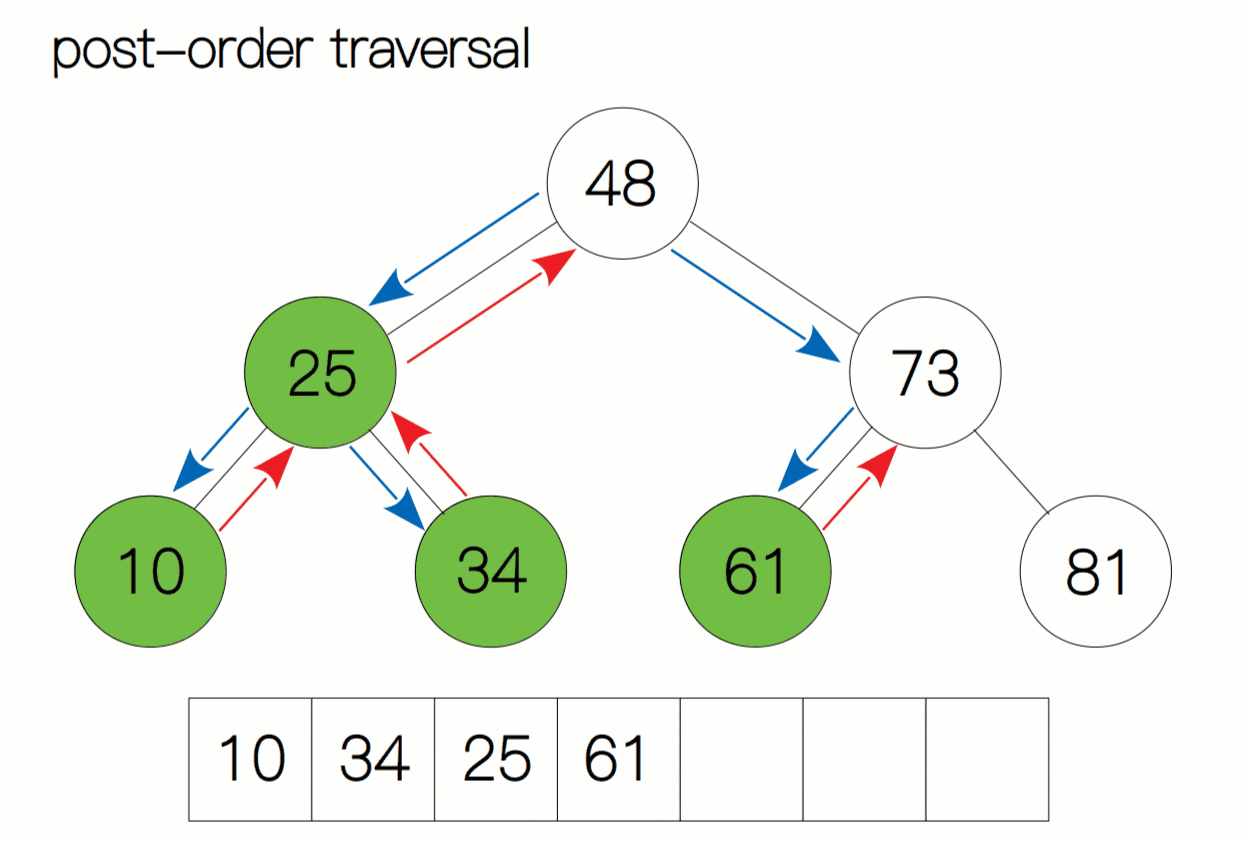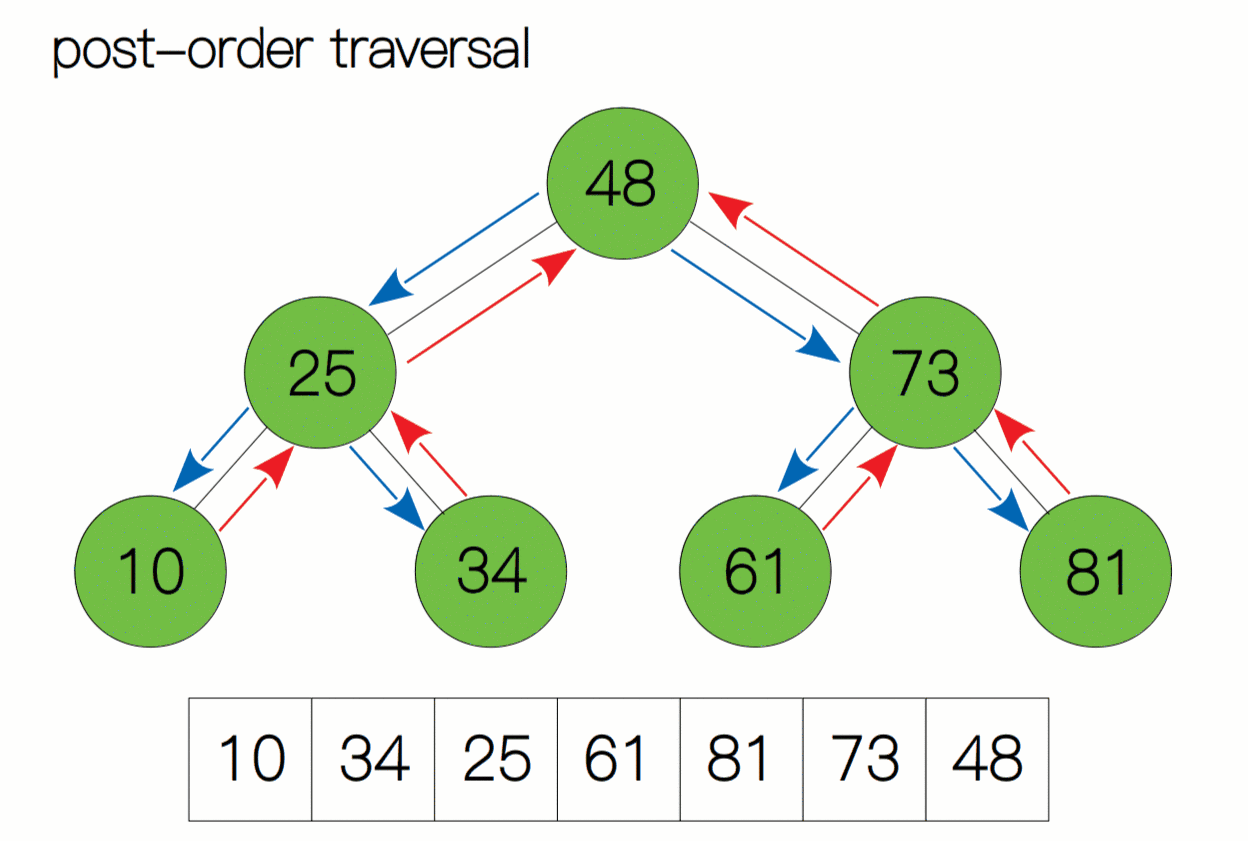
后序遍历代码及注释：

// 后序遍历
void PrintPostOrder(BTNode* root)
{// 如果当前节点为空，直接返回if (!root){return;}// 递归调用后序遍历函数，遍历左子树PrintPostOrder(root->left);// 递归调用后序遍历函数，遍历右子树PrintPostOrder(root->right);// 打印当前节点的数据printf("%c ", root->data);
}

4、层序遍历

层序遍历是二叉树中最常用的遍历方法之一，它依次按层遍历二叉树中的结点。

具体实现思路如下：

创建一个队列，将根节点插入队列中。
取出队列的首个节点，访问该节点。
若该节点有左子节点，将左子节点插入队列中。
若该节点有右子节点，将右子节点插入队列中。
重复步骤 2 ~ 4，直到队列为空为止。

层序遍历代码及注释：

typedef char BTDataType;  // 二叉树中每个节点所存储的数据类型为 chartypedef struct BTNode
{BTDataType data;  // 节点存储的数据struct BTNode* left;  // 左子节点struct BTNode* right;  // 右子节点
}BTNode;  // 定义二叉树结构体typedef BTNode* QueueDataType;  // 队列中每个节点所存储的数据类型为 BTNode 指针typedef struct QNode
{QueueDataType val;  // 节点存储的数据struct QNode* next;  // 指向下一个节点的指针
}QNode;  // 定义队列节点结构体typedef struct Queue
{QNode* front;  // 队头指针QNode* rear;  // 队尾指针int size;  // 队列中元素的个数
}Queue;  // 定义队列结构体// 初始化队列
void QueueInit(Queue* q)
{assert(q);q->front = NULL;q->rear = NULL;q->size = 0;
}// 入队
void QueuePush(Queue* q, QueueDataType x)
{assert(q);QNode* temp = (QNode*)malloc(sizeof(QNode));if (temp == NULL){perror("malloc fail!");exit(-1);}temp->val = x;temp->next = NULL;if (q->front == NULL){q->front = q->rear = temp;  // 队列为空时，新元素既是队头也是队尾}else{q->rear->next = temp;  // 把新元素连接到队尾后q->rear = temp;  // 更新队尾指针为新的元素}q->size++;  // 队列元素个数加1
}// 判断队列是否为空
bool QueueEmpty(Queue* q)
{assert(q);if (q->front == NULL){return true;  // 队列为空}return false;  // 队列不为空
}// 获取队头元素
QueueDataType QueueTop(Queue* q)
{assert(q);if (!QueueEmpty(q)){return q->front->val;  // 返回队头元素的值}else{printf("队空，无法获取队头元素！\n");exit(-1);}
}// 出队
void QueuePop(Queue* q)
{assert(q);if (!QueueEmpty(q)){QNode* temp = q->front;  // 保存队头指针q->front = q->front->next;  // 移动队头指针到下一个元素free(temp);  // 释放原队头节点的内存空间q->size--;  // 队列元素个数减1}else{printf("队空，无法删除队头元素！\n");exit(-1);}
}// 获取队列元素个数
int QueueSize(Queue* q)
{assert(q);return q->size;  // 返回队列元素个数
}// 二叉树的层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{assert(root);Queue q;QueueInit(&q);  // 初始化队列QueuePush(&q, root);  // 将根节点入队int TSize = 1;while (!QueueEmpty(&q)){// 遍历当前层级的结点while (TSize > 0){BTNode* cur = QueueTop(&q);  // 获取队头元素QueuePop(&q);  // 出队printf("%c ", cur->data);  // 输出当前结点的数据if (cur->left){QueuePush(&q, cur->left);  // 左子节点入队}if (cur->right){QueuePush(&q, cur->right);  // 右子节点入队}TSize--;  // 减少当前层级元素个数}printf("\n");  // 输出换行符表示当前层级遍历结束TSize = QueueSize(&q);  // 更新当前层级元素个数}
}