文章目录
- 前言
- 代码模拟梯度下降
- 构建函数与导函数
- 函数的可视化
- 求这个方程的最小值(直接求导)
- 求方程最小值(不令方程导为0)【梯度下降】
- eta=0.1
- eta = 0.2
- eta = 50
- eta = 0.01
- 画出eta=0.1时的梯度下降x的变化过程
- 总结
前言
💫你好,我是辰chen,本文旨在准备考研复试或就业
💫本文内容来自某机构网课,是我为复试准备的第一个项目
💫欢迎大家的关注,我的博客主要关注于考研408以及AIoT的内容
🌟 预置知识详见我的AIoT板块,需掌握 基本Python语法, Numpy, Pandas, Matplotlib
以下的几个专栏是本人比较满意的专栏(大部分专栏仍在持续更新),欢迎大家的关注:
💥ACM-ICPC算法汇总【基础篇】
💥ACM-ICPC算法汇总【提高篇】
💥AIoT(人工智能+物联网)
💥考研
💥CSP认证考试历年题解
代码模拟梯度下降
import numpy as np
import matplotlib.pyplot as plt
构建函数与导函数
f = lambda x : (x - 3.5) ** 2 - 4.5 * x + 10
# 导函数
g = lambda x : 2 * (x - 3.5) - 4.5
函数的可视化
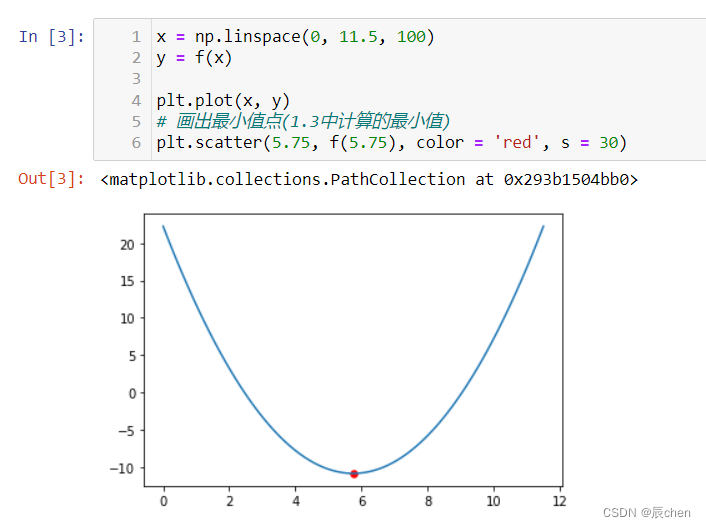
x = np.linspace(0, 11.5, 100)
y = f(x)plt.plot(x, y)
# 画出最小值点(5.75即为最小值点,具体计算即为令导数为0,见下个代码块)
plt.scatter(5.75, f(5.75), color = 'red', s = 30)
求这个方程的最小值(直接求导)
'''
令导数值 = 0
2 * (x - 3.5) - 4.5 = 0
2 * x = 11.5
x = 5.75
'''
求方程最小值(不令方程导为0)【梯度下降】
eta=0.1
# 给一个步幅,也就是学习率
eta = 0.1 # 正解为 x = 5.75, 若我们梯度下降求得的 x = 5.749, 5.7501 ... 亦是正确答案(很接近)
x = np.random.randint(0, 12, size = 1)[0]# 多次 while 循环,每次梯度下降,记录一下上一次的值,规定一个精确度进行比较
# +0.1; +0.2; +1;...都是可以的,是为了让他们在一开始有差异
last_x = x + 0.1# 下面自定义一个精确度
precision = 0.0001
print('-----------------随机的x是:', x)while True:if np.abs(x - last_x) < precision: # 退出死循环条件:更新时变化甚微break# 更新,梯度下降last_x = xx = x - eta * g(x)print('+++++++++++++++++更新之后的x是:', x)
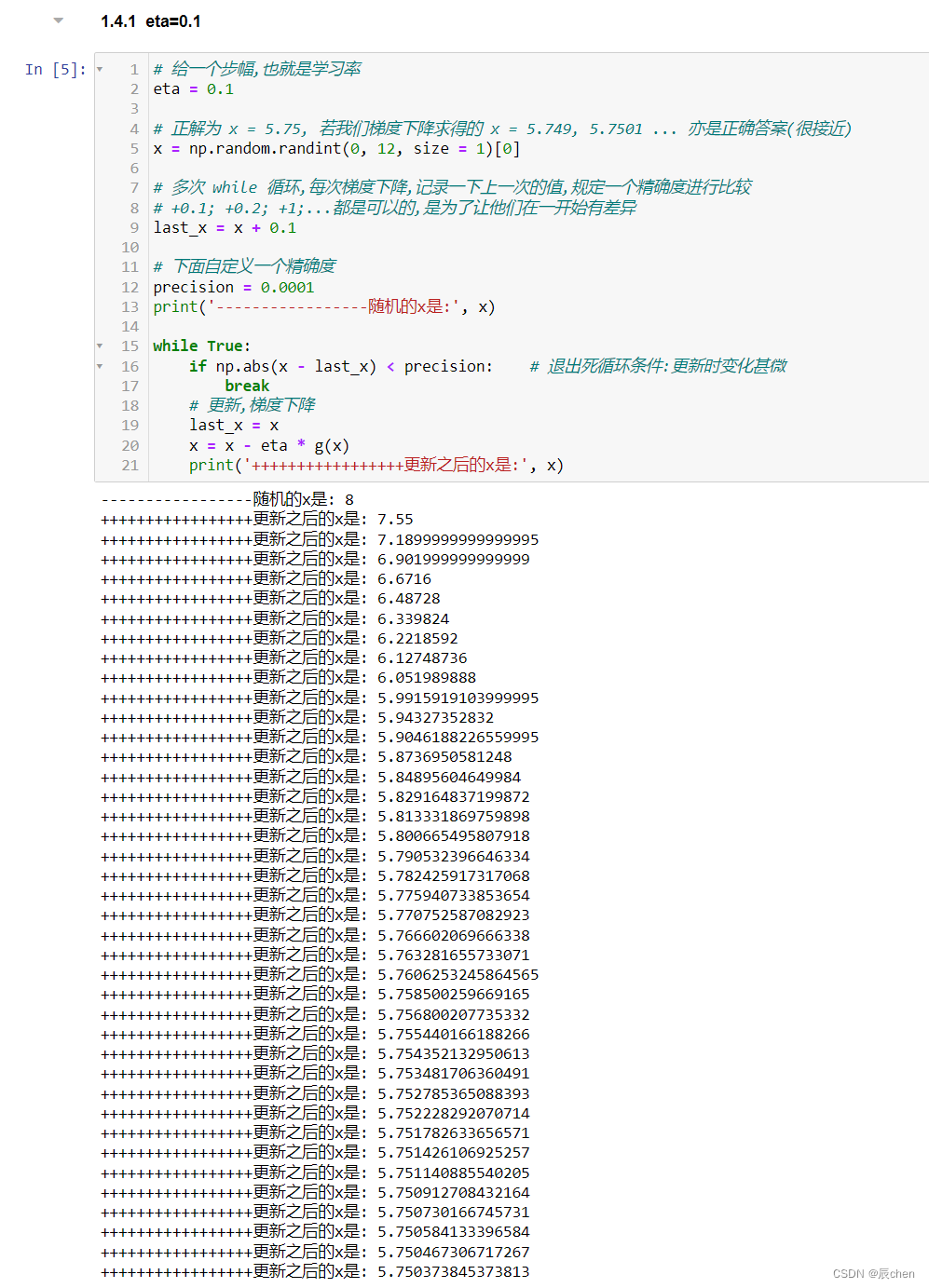
可以看到,最终逼近的结果为 5.750373845373813,可以认为是正确解
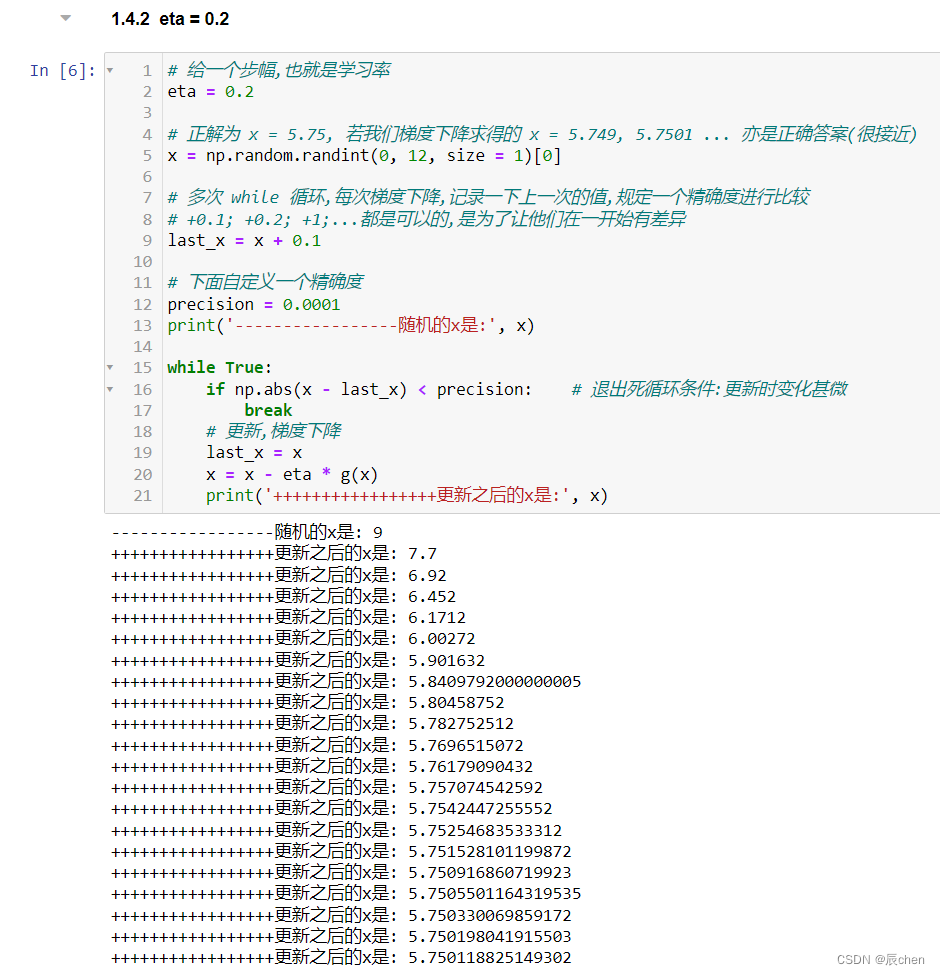
eta = 0.2
把 eta 调大之后,可以明显观察到收敛的快了
# 给一个步幅,也就是学习率
eta = 0.2# 正解为 x = 5.75, 若我们梯度下降求得的 x = 5.749, 5.7501 ... 亦是正确答案(很接近)
x = np.random.randint(0, 12, size = 1)[0]# 多次 while 循环,每次梯度下降,记录一下上一次的值,规定一个精确度进行比较
# +0.1; +0.2; +1;...都是可以的,是为了让他们在一开始有差异
last_x = x + 0.1# 下面自定义一个精确度
precision = 0.0001
print('-----------------随机的x是:', x)while True:if np.abs(x - last_x) < precision: # 退出死循环条件:更新时变化甚微break# 更新,梯度下降last_x = xx = x - eta * g(x)print('+++++++++++++++++更新之后的x是:', x)
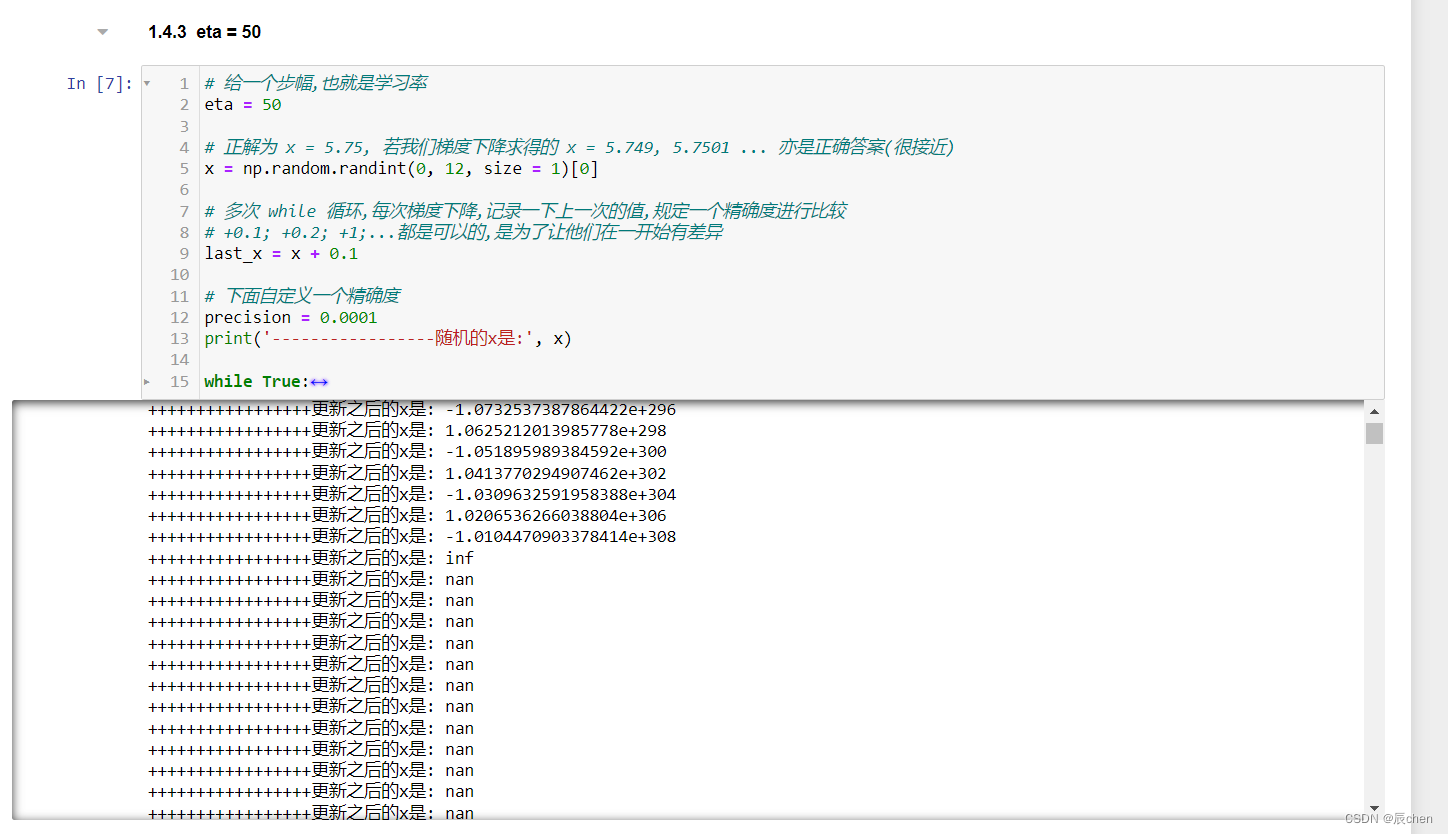
eta = 50
当然,eta 的值也不可以设的过大,会造成发散
# 给一个步幅,也就是学习率
eta = 50# 正解为 x = 5.75, 若我们梯度下降求得的 x = 5.749, 5.7501 ... 亦是正确答案(很接近)
x = np.random.randint(0, 12, size = 1)[0]# 多次 while 循环,每次梯度下降,记录一下上一次的值,规定一个精确度进行比较
# +0.1; +0.2; +1;...都是可以的,是为了让他们在一开始有差异
last_x = x + 0.1# 下面自定义一个精确度
precision = 0.0001
print('-----------------随机的x是:', x)while True:if np.abs(x - last_x) < precision: # 退出死循环条件:更新时变化甚微break# 更新,梯度下降last_x = xx = x - eta * g(x)print('+++++++++++++++++更新之后的x是:', x)
这是一个死循环
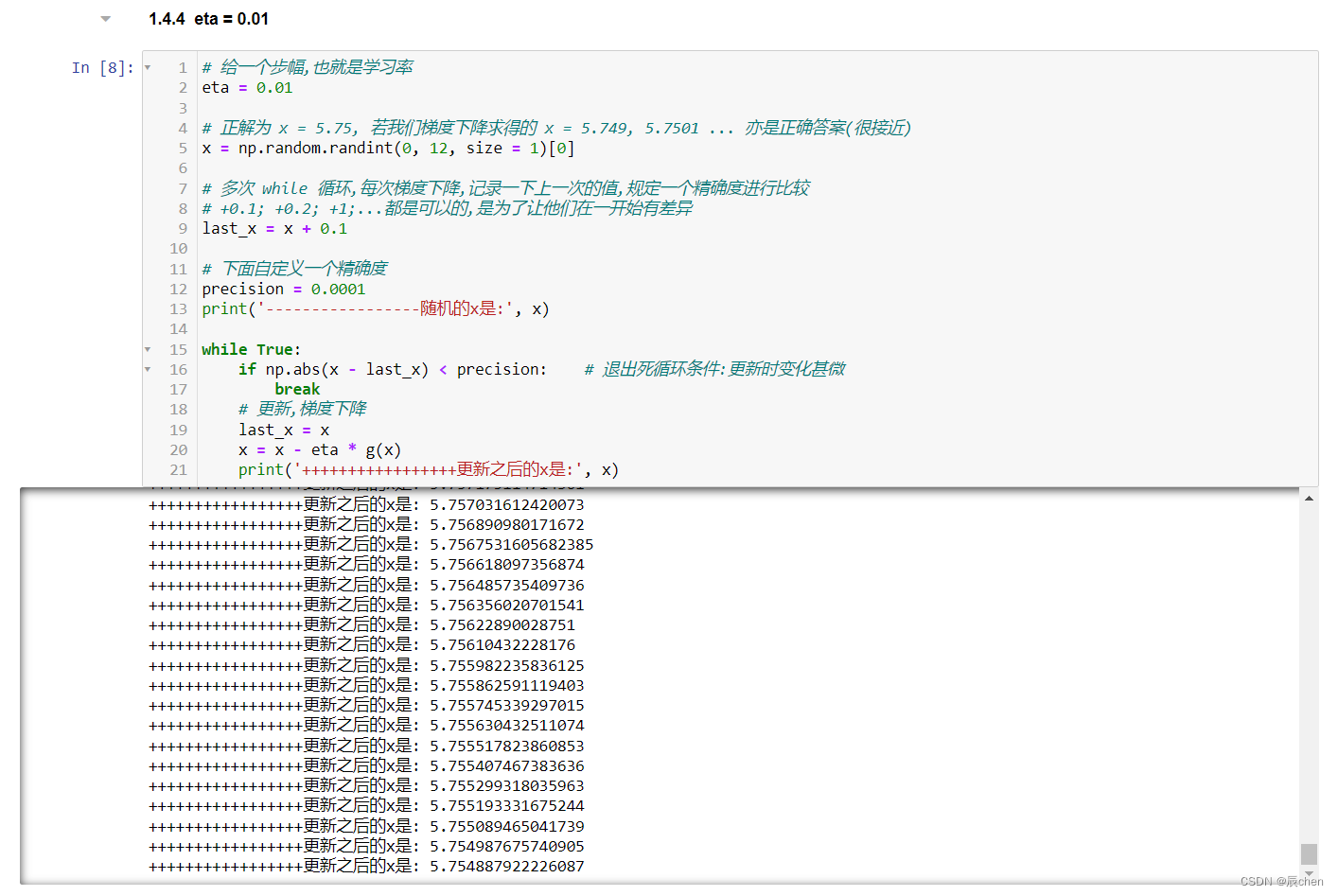
eta = 0.01
如果 eta 的值设的比较小,会收敛,但是会很慢
# 给一个步幅,也就是学习率
eta = 0.01# 正解为 x = 5.75, 若我们梯度下降求得的 x = 5.749, 5.7501 ... 亦是正确答案(很接近)
x = np.random.randint(0, 12, size = 1)[0]# 多次 while 循环,每次梯度下降,记录一下上一次的值,规定一个精确度进行比较
# +0.1; +0.2; +1;...都是可以的,是为了让他们在一开始有差异
last_x = x + 0.1# 下面自定义一个精确度
precision = 0.0001
print('-----------------随机的x是:', x)while True:if np.abs(x - last_x) < precision: # 退出死循环条件:更新时变化甚微break# 更新,梯度下降last_x = xx = x - eta * g(x)print('+++++++++++++++++更新之后的x是:', x)
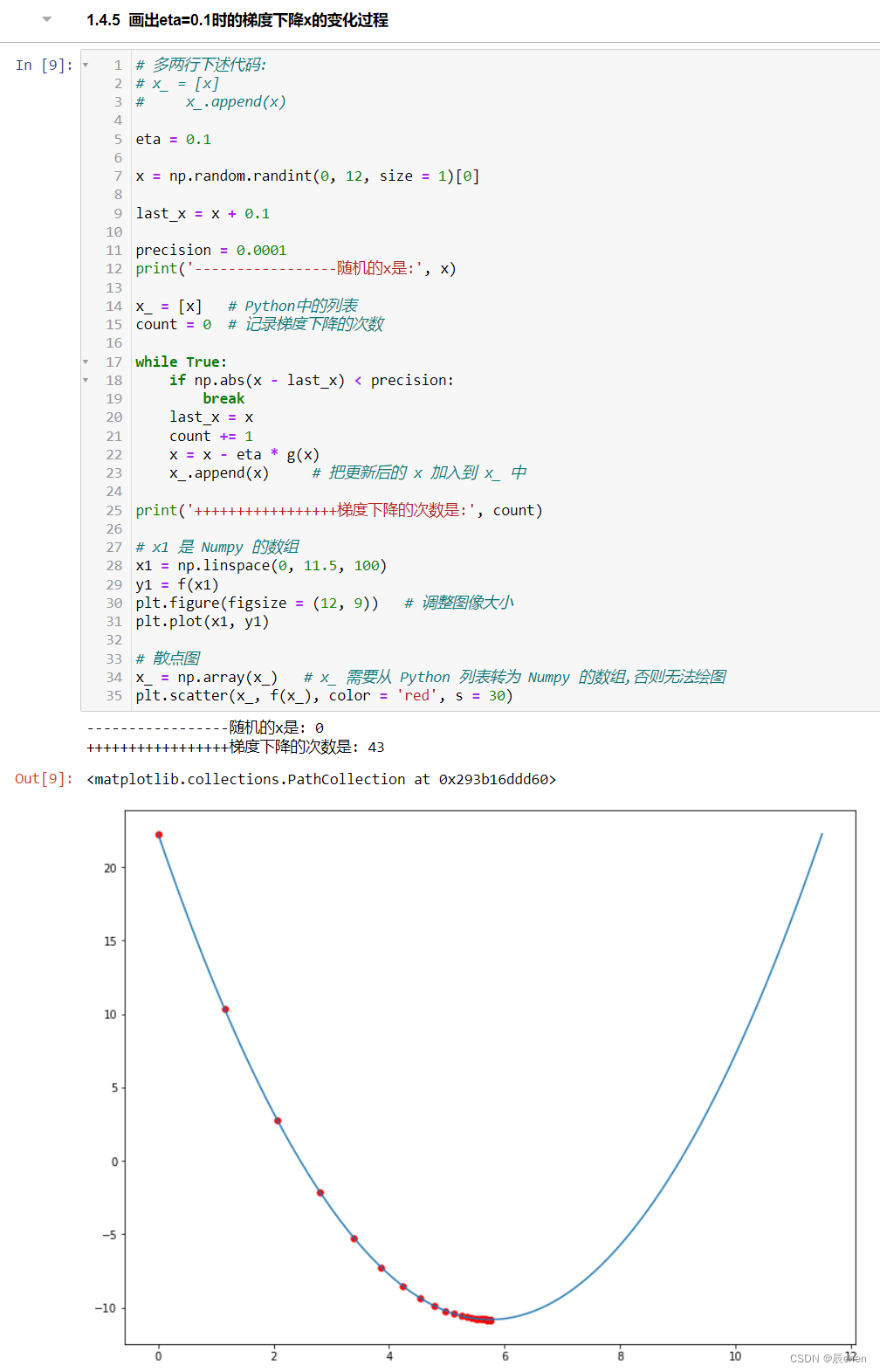
画出eta=0.1时的梯度下降x的变化过程
# 多两行下述代码:
# x_ = [x]
# x_.append(x)eta = 0.1 x = np.random.randint(0, 12, size = 1)[0]last_x = x + 0.1precision = 0.0001
print('-----------------随机的x是:', x)x_ = [x] # Python中的列表
count = 0 # 记录梯度下降的次数while True:if np.abs(x - last_x) < precision: breaklast_x = xcount += 1x = x - eta * g(x)x_.append(x) # 把更新后的 x 加入到 x_ 中print('+++++++++++++++++梯度下降的次数是:', count)# x1 是 Numpy 的数组
x1 = np.linspace(0, 11.5, 100)
y1 = f(x1)
plt.figure(figsize = (12, 9)) # 调整图像大小
plt.plot(x1, y1)# 散点图
x_ = np.array(x_) # x_ 需要从 Python 列表转为 Numpy 的数组,否则无法绘图
plt.scatter(x_, f(x_), color = 'red', s = 30)
总结
模拟的时候还发现了 eta 设置的过小算出来的值也是错误的现象,知道了原因后会补在这里