内容参考于:三分钟音乐社
上一个内容:87.乐理基础-记号篇-反复记号(一)反复、跳房子-CSDN博客
下图红色左括号框起来的东西,它们都相对比较抽象一点,这几个词都是意大利语
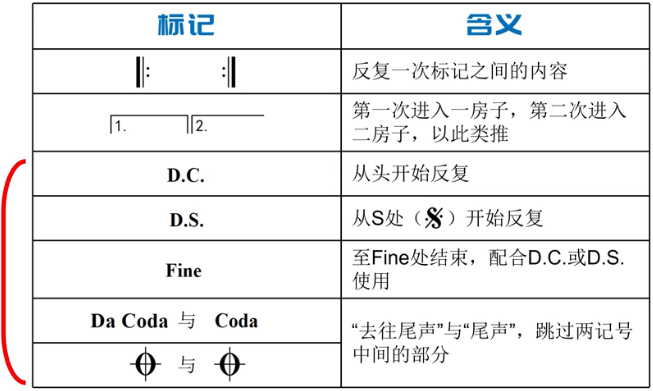
首先D.C.这个标记,然后把D.C.单独拿出来,如图1,D.C.不同的写法看图10
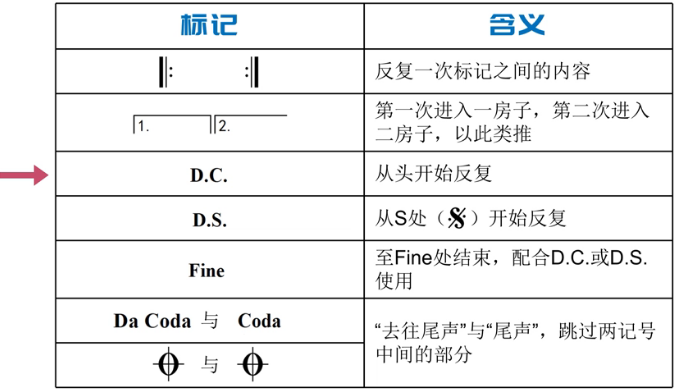
D.S.然后看图14
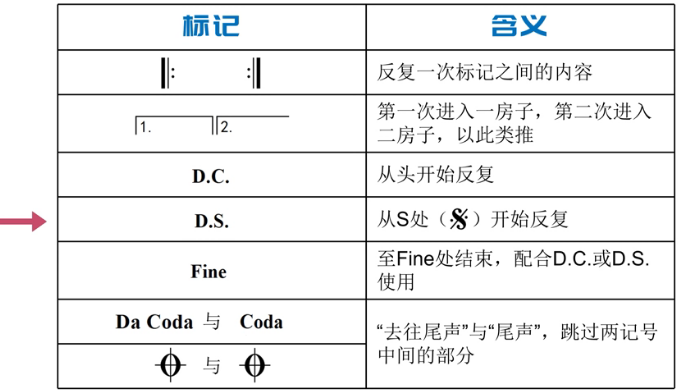
图1:意思就是从头反复,也就是遇到这个东西之后就要从头开始去演奏,演奏到什么时候为止,又分为两种情况,第一种情况在乐谱中遇见某一个地方写了一个Fine,那就从头演奏到Fine这个地方就全曲结束,也就是见到D.C.就从头演奏一直到Fine这个地方就全曲结束,实际的例子如图2,第二种情况乐谱中不会出现Fine,因为可能需要连接一段尾声( 意文为Coda),如图11,这个第二种也就是从头反复至Da Coda,然后跳到Coda处继续演奏,这时D.C.可能会写成D.C. al Coda,然后上方表里的东西都通过D.C.把Fine、Da Coda 与 Coda、圈加十字都写完了,就还剩一个D.S.,第一种情况的第三种写法是D.C. al Fine,第二种情况的第三种写法是D.C. al Coda,详情看图10哪里的说明,图10位置只写了第一种情况的第三种写法说明,但是第二种写法的说明与它意思一样

图2:遇到D.C.从头演奏之后Fine才会生效,然后乐谱写法,通常D.C.是写在乐谱下方,而Fine写在乐谱上方,就像下图的样子,但是即便是把D.C.写在了上方,或者把Fine写在了下方,这也是都有可能的算不上什么错误,对乐谱实际上该怎样演奏都没任何影响的,这是第一点,第二点,这个D.C.对应的是终止线,那也可能有的谱写的是 后反复记号,如图3

图3:然后毕竟D.C.表示从头反复,但一个后反复记号也表示从头反复,这两种都表示从头反复的记号叠在一起并非是双重效果,最多算是一种强调作用,实际上仍然只是从头反复一次到Fine就结束了,如图2所示,然后D.C.位置还可能是单小节线,如图4
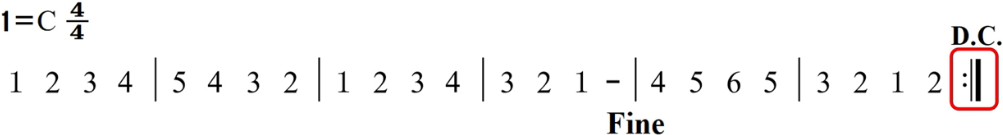
图4:因为虽然乐谱从外观上看上去好像这里是最后了,但实际上音乐并没有真正结束,所以有的谱可能并不会在这里画终止线,而只是画一根小节线,还有可能是画双竖线,如图5

图5:这种两根窄竖线的线,它没有一个明确的名字,如图6,那D.C.这里的确是可以写双竖线,毕竟音乐也没有真正结束,音乐又重新从头开始反复第二遍,那也有一种分节、分段的感觉。然后D.C.这个地方并没有结束,所以可以不用画终止线,那有些谱可能就会在Fine对应的地方写上终止线,因为Fine这个地方才是真正结束的地方,如图9

图6:叫下方的任意一个都可以,它主要作用是拿来提示音乐分节或者分段了,如图7

图7:比如一首音乐从C调转到G调,那它在乐谱上,就会在转掉的这个地方写双竖线,给一种音乐分节、分段的感觉,但并不是说双竖线的这个地方要停顿一下,只是提示这里转调了,所以画跟双竖线提示这里音乐分段了,但是这种地方,不写双竖线,仍然只是普通的一根小节线,比如图8

图8:就是由图7的双竖线变成了图8的小节线,这也是没问题的,并不是一定要写成上面那种双竖线的,然后回到图5

图9:那些终止线也不是完全没有道理的,所以说,关于D.C.和Fine它们所对应的位置处的,不同的乐谱可能写的是不同的线,不管它画什么线,实际效果都是一模一样的,都是到了D.C.之后从头反复,然后到Fine出结束,所以不要去纠结线的问题,有D.C.和Fine直接看D.C.和Fine就好,那些线怎样画都不重要。

图10:D.C.是第一种写法,Da Capo是第二种写法,第三种写法叫做Da Capo al Fine简称D.C. al Fine,第三种写法是要把配合乐谱中有fine的时候才会使用的

图11:乐谱中是没有Fine的,首先还是从头开始演奏,然后到D.C.之后,就意味着又要从头开始反复,这个时候没有Fine了,这时就要一直进行到Da Coda这个地方,Coda的意思是尾声,Da Coda就是去往尾声的意思,如图12

图12:所以到了Da Code这个地方,我们就要直接跳过Da Coda和Coda中间的段落,直接从Coda处继续,然后一直到结束,然后Da Coda和Coda其它写法,如图13

图13:

或者直接用下图中的两个符号来代替,符号是一个圈和一个十字的组合,虽然这两个标记一样,但实际上前面这个标记意味着DaCoda,去往尾声,后面这个标记实际上意味着Coda,也就是尾声,所以Da Coda和Coda是一个配套的组合

然后还会有,标记加字母的写法,如下图,都是一样的意思,反正遍的时候就跳过Da Coda和Coda中间的内容就好了

图14:D.S.意思是从S处反复,所以遇到D.S.之后就要去找到乐谱中哪里标了S,要注意,这个S的标记在乐谱上其实不是S这个字母,所谓的S样子看图15,反复到什么位置结束呢?D.C.有两种情况那么D.S.也是有两种情况,两种情况都是与D.C.一样的,比如图16的乐谱

图15:也就是s的身上有一个百分号

图16:D.S.与D.C.的区别就是D.S.比D.C.多了一个S的标记而已,其它的细节都是一样的,第一种情况就是和Fine的搭配,到了D.S.之后就从S处开始反复,到Fine就全曲结束,D.S.第二种情况就是配合Da Coda和Coda了,看图17
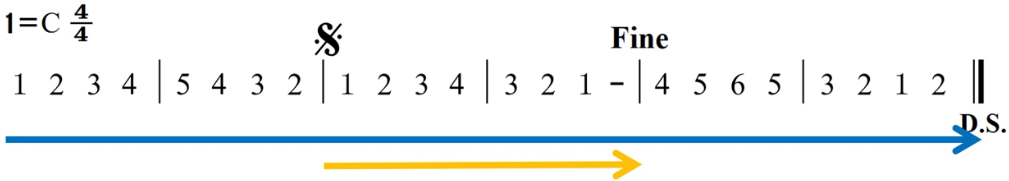
图17:从S处开始反复到Da Coda处然后直接跳过Da Coda与Coda中间的段落,直接从Coda处继续演奏,直到结束,它与D.C.一样的意思

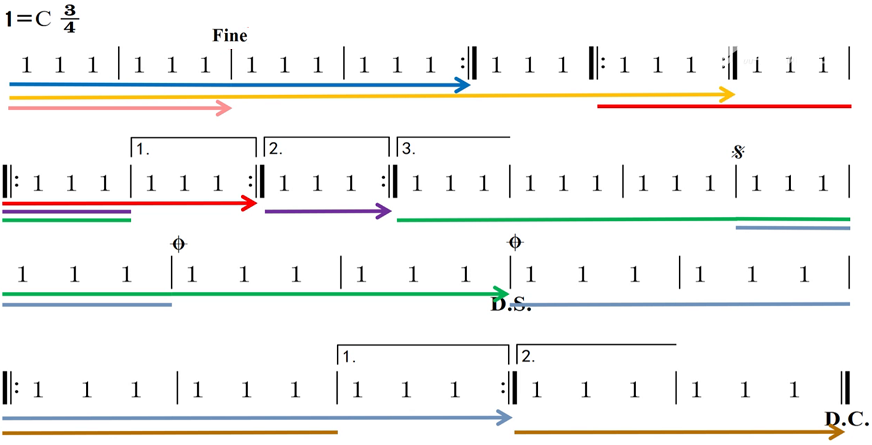
带有所有反复记号的乐谱例子:


![[足式机器人]Part2 Dr. CAN学习笔记 - Ch02动态系统建模与分析](https://img-blog.csdnimg.cn/direct/630219cc3a314904ba754366a8add31b.png#pic_center)