零、前言

关于二分图的基本知识见：二分图及染色法判定

---

一、红娘牵线

一位红娘近日遇到一群暧昧男女，被请求成全他们，经验丰富的红娘观察到一名男生可能有多名青睐的女生，一名女生也可能有多名青睐的男生，但是出于道德伦理要求，显然只能两两男女配对，为了尽可能使大家满意，她要尽可能地成全多对男女。经过观察，她发现这些男女间地暧昧关系如下（连线代表互相青睐）：

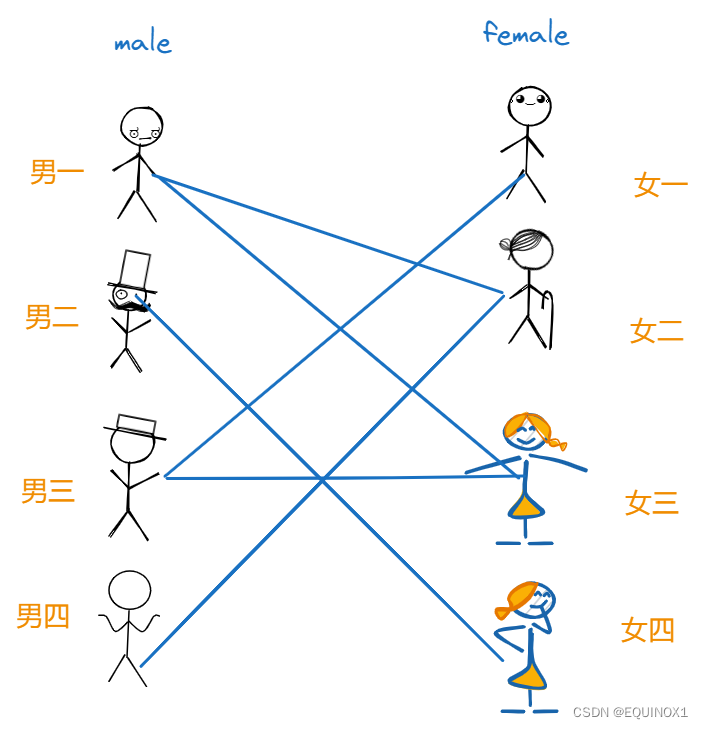
红娘根据经验快速地进行了一次配对，男一配女二，男儿配女四，男三配女三。

（下图红色连线代表配对，此时女一和男四没有配对）

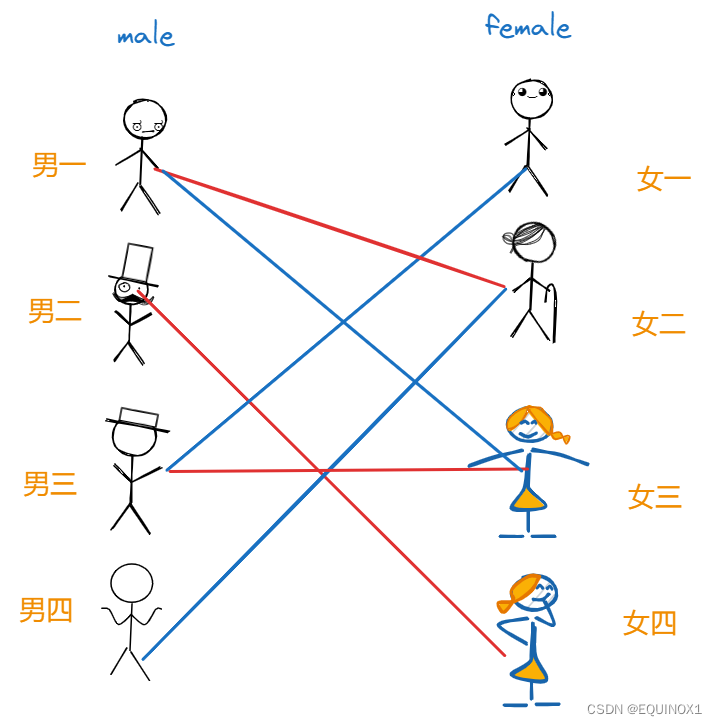
配对的三对男女自然很满意，此时女一和男四悻悻地来找红娘，说他们两个怎么办，红娘看二人不愿凑合都想有心仪的归宿，男四只愿跟女二在一起，女一只愿跟男三在一起。

红娘于是只得回头看已经配对的三对男女，发现男一似乎对女三也有意思，但是女三已经跟男三配对了，于是红娘私底下找到男三，问他愿不愿意将女三让给男一，自己可以帮他跟女一牵线，男三一看这敢情好，直接答应，于是男三的对象变为了女一，男一的对象变为了女三，男四趁虚而入，和女二配对，于是有了下面的局面：

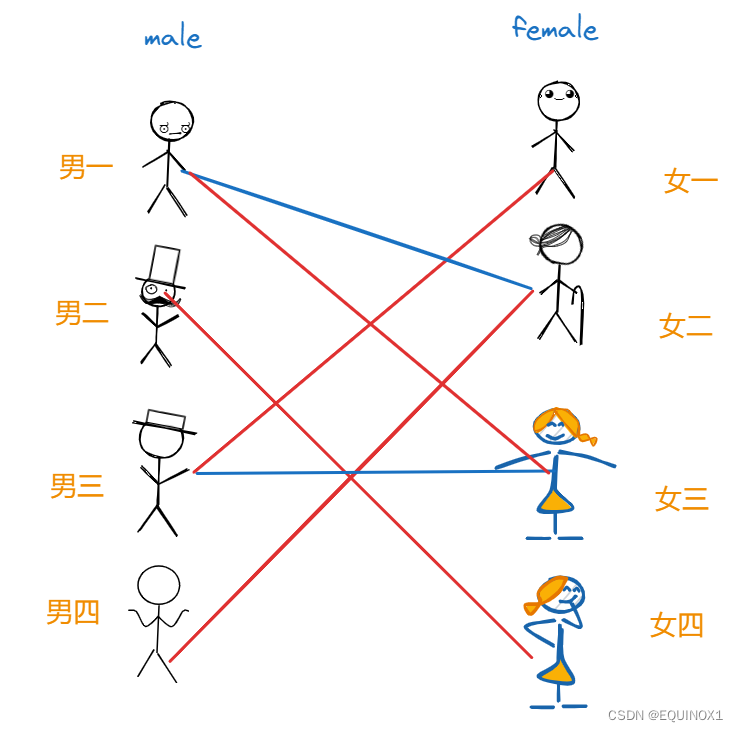
至此，每个人都有和自己的心仪对象之一配了对，中间虽有ntr波折，但结局皆大欢喜。

---

二、二分图最大匹配

2.1概念

“任意两条边都没有公共端点”的边的集合被称为图的一组匹配。在二分图中，包含边数最多的一组匹配被称为二分图的最大匹配。

上面的红娘牵线其实就是二分图的最大匹配的形象示例。

我们称匹配的边为匹配边，匹配边的两个端点为匹配点，相应的自然有了非匹配边和非匹配点的概念。

2.2交替路

从一个非匹配点出发，依次经过非匹配边、匹配边、非匹配边形成的路径叫交替路。

2.3增广路

从一个未匹配点出发，走交替路，若能到达另一个未匹配点，则这条交替路称为增广路。

增广路显然有如下性质：

1. 长度len为奇数
2. 路径上第1、3、5……len条边是非匹配边，第2、4……len - 1条边是匹配边

正因为以上性质，如果我们把路径上所有边的状态取反，原来的匹配边变成非匹配边，原来的非匹配边变成匹配边，那么得到的新的边集仍然是一组匹配，并且匹配边数+1.

从而得到以下推论：

二分图的一组匹配是最大匹配，当且仅当图中不存在包含该匹配的增广路。

2.4匈牙利算法

**匈牙利算法（Hungary Algorithm）**又称牛头人算法增广路算法，用于计算二分图的最大匹配。

2.4.1算法原理

算法流程十分简单：

1. 设匹配边集S = Ø，即所有边都是非匹配边
2. 找到增广路path，将增广路上所有边状态取反，得到更大的匹配S‘
3. 重复2，直到没有增广路

算法的关键在于如何找到增广路。

我们将二分图的点分为左部节点和右部节点，匈牙利算法依次尝试给给每一个左部节点u寻找一个匹配的右部节点v。右部节点v能和左部节点u匹配需要满足以下两个条件之一：

1. v本身就是非匹配点
   1. 此时u~v为长度为1的增广路
2. v已经跟左部节点u’匹配，但是从u‘出发能找到另一个右部节点v’和其匹配。
   1. 此时u_vu‘~v’就是一条增广路

在具体的程序实现中，我们采用深度优先搜索的框架，递归的从u出发去找增广路，若找到，则在回溯时，正好把路径上的匹配状态取反。另外，可以用全局标记数组来维护节点的访问情况，避免重复搜索。

匈牙利算法的正确性基于贪心策略，它的一个重要特点是：当一个节点成为匹配点后，至多因为找到增广路而更换匹配对象，但是绝不会再变回非匹配点。
对于每个左部节点，寻找增广路最多遍历整张二分图一次。因此,该算法的时间复杂度为O(nm)，其中n为点数目，m为边数目。

2.4.2算法示例

有二分图如下，左部节点1、2、3、4，右部节点1、2、3、4

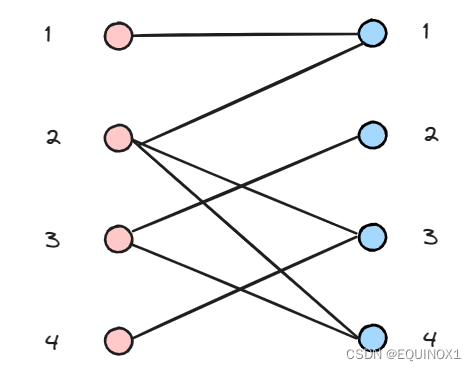
左1匹配右1

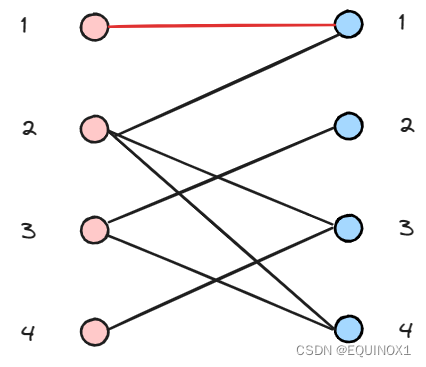
左2尝试匹配右1失败

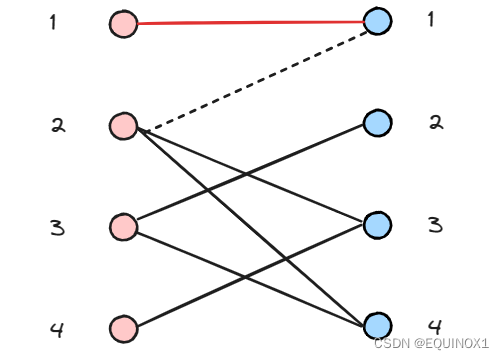
左2匹配右3

左3匹配右2

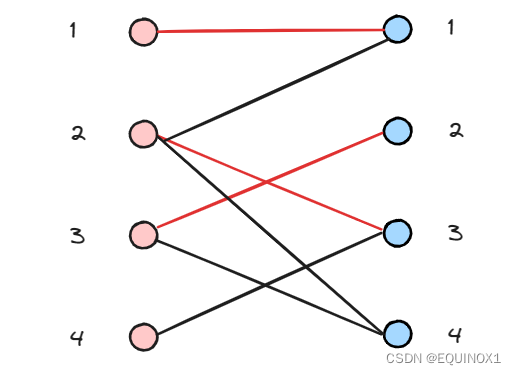
左4尝试匹配右3，递归左2尝试匹配右1失败

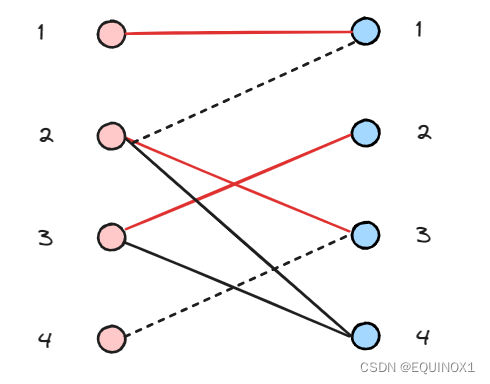
左2继续尝试匹配右4，成功找到增广路

回溯时把增广路取反，左4得以匹配右3

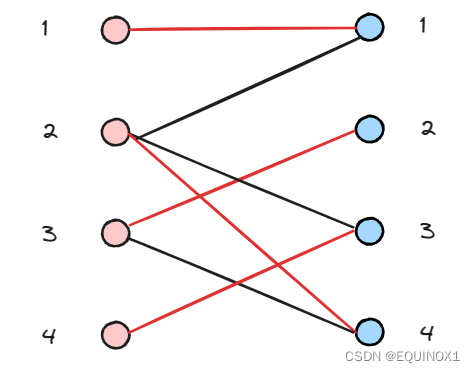
2.4.3代码实现

bool dfs(int u)
{for (int i = head[u]; ~i; i = edges[i].nxt){int v = edges[i].v;if (vis[v])continue;vis[v] = 1;if (!match[v] || dfs(match[v])){match[v] = u;return true;}}return false;
}
//main
for (int i = 1; i <= n; i++)
{memset(vis, 0, sizeof(vis));if (dfs(i))cnt++;
}

---

3.OJ练习

二分图匹配的模型有两个要素：
1.节点能分成独立的两个集合，每个集合内部有0条边。
2.每个节点只能与1条匹配边相连。
我们把它简称为“0要素”和“1要素”。在把实际问题抽象成二分图匹配时，我们就要寻找题目中具有这种“0”和“1”性质的对象，从而发现模型构建的突破口。

3.1模板

P3386 【模板】二分图最大匹配 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

洛谷模板题，检验以下自己的匈牙利算法板子是否正确，以便于在后续问题中使用。

#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <string>
using namespace std;
using pii = pair<int, int>;
#define N 510
#define M 50010
struct edge
{int v, nxt;
} edges[M << 1];
int head[N], match[N]{0}, idx = 0, n, m, e, a, b, cnt = 0;
bool vis[N];
void addedge(int u, int v)
{edges[idx] = {v, head[u]};head[u] = idx++;
}
bool dfs(int u)
{for (int i = head[u]; ~i; i = edges[i].nxt){int v = edges[i].v;if (vis[v])continue;vis[v] = 1;if (!match[v] || dfs(match[v])){match[v] = u;return true;}}return false;
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);// freopen("in.txt", "r", stdin);// freopen("out.txt", "w", stdout);memset(head, -1, sizeof(head));cin >> n >> m >> e;for (int i = 1; i <= e; i++){cin >> a >> b;addedge(a, b);}for (int i = 1; i <= n; i++){memset(vis, 0, sizeof(vis));if (dfs(i))cnt++;}cout << cnt;return 0;
}

3.2棋盘覆盖

372. 棋盘覆盖 - AcWing题库

首先对于一个矩阵而言，我们根据行列坐标相加的奇偶性可以对其进行二染色，并且任何一个格子和其四个方向上的相邻格子颜色不同。

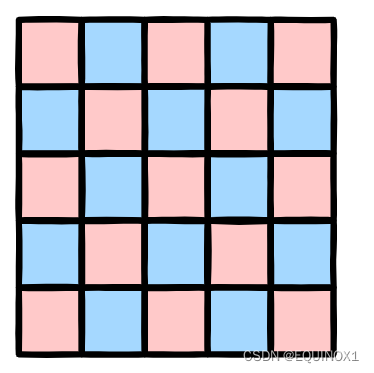
这样我们就可以将问题抽象为二分图匹配问题。

0要素：同色格子之间无边 1要素：每个格子只能被一张骨牌覆盖

一个骨牌一定是覆盖了两个颜色不同的方格，我们按照颜色将格子分为左部点和右部点，被骨牌覆盖的两个左右部点即为一个匹配，求最多的骨牌数目就是求最大匹配。

基本上还是板子题，由于数据量很小所以用了邻接矩阵，由于有的格子不能放置，所以要加个条件。

奇数格子还是偶数格子作为左部点没有区别。

直接看代码：

#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <string>
using namespace std;
using pii = pair<int, int>;
#define N 110
#define M 50010
int n, t, a, b, cnt = 0, dir[5]{1, 0, -1, 0, 1};pii match[N][N];
bool g[N][N], vis[N][N];
bool dfs(int x, int y)
{for (int i = 0; i < 4; i++){int nx = x + dir[i], ny = y + dir[i + 1];int pos = (nx - 1) * n + ny;if (nx < 1 || ny < 1 || nx > n || ny > n || vis[nx][ny] || g[nx][ny])continue;vis[nx][ny] = 1;if (match[nx][ny].first == -1 || dfs(match[nx][ny].first, match[nx][ny].second)){match[nx][ny] = {x, y};return true;}}return false;
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);memset(g, 0, sizeof(g));memset(match, -1, sizeof(match));cin >> n >> t;while (t--){cin >> a >> b;g[a][b] = 1;}for (int i = 1; i <= n; i++){for (int j = (i & 1) ? 1 : 2; j <= n; j += 2){if (!g[i][j]){memset(vis, 0, sizeof(vis));if (dfs(i, j))cnt++;}}}cout << cnt;return 0;
}

3.3車的放置

373. 車的放置 - AcWing题库

1要素：每行每列只能有一个车，对于(i,j)放置车，相当于i行j列都被占用，即i行和j列连边

0要素：一个车不能既在第i行又在第j行，所以行与行之间无边

#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <string>
using namespace std;
using pii = pair<int, int>;
#define N 210
#define M 50010
int n, m, t, a, b, cnt = 0, dir[5]{1, 0, -1, 0, 1};int match[N]{0};
bool g[N][N]{0}, vis[N];
bool dfs(int i)
{for (int j = 1; j <= m; j++){if (g[i][j] || vis[j])continue;vis[j] = 1;if (!match[j] || dfs(match[j])){match[j] = i;return true;}}return false;
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);cin >> n >> m >> t;while (t--){cin >> a >> b;g[a][b] = 1;}for (int i = 1; i <= n; i++){memset(vis, 0, sizeof(vis));if (dfs(i))cnt++;}cout << cnt;return 0;
}