奇异值分解在图形压缩中的应用

---

在研究奇异值分解的工程应用之前，我们得明白什么是奇异值？什么是奇异向量？

奇异值与奇异向量

概念：奇异值描述了矩阵在一组特定向量上的行为，奇异向量描述了其最大的作用方向。

奇异值分解(SVD)

矩阵A的分解涉及一个$m\times n$的矩阵$\Sigma$,其中$\Sigma$=$\left[\begin{array}{cc}D& 0\\ 0& 0\end{array}\right]$,D是一个$r\times r$的方阵$(r\le m,r\le n)$

定理：设A是秩为$r$的$m\times n$的矩阵，那么存在一个类似于$\Sigma$的矩阵，其中$D$的对角线元素是 $A$的前$r$个奇异值，${\sigma }_1\ge {\sigma }_2\ge {\sigma }_3\ge ...\ge {\sigma }_r>0$并且存在一个$m\times m$的正交矩阵$U$ 和一个 $n\times n$的正交矩阵$V^T$使得$A=U\Sigma V^T$

奇异值分解计算过程

我们先假设一个矩阵$A=\left[\begin{array}{cc}2& 3\\ 0& 2\end{array}\right]$
设$U=[u_1{u}_2{u}_3...]$ , $\sum =diag[{\sigma }_1{\sigma }_2{\sigma }_3...]$ , $V={\left[\begin{array}{c}{v}_1\\ v_2\\ v_3\\ ...\end{array}\right]}^T$
其中$U$代表A的正交矩阵；$\sum$代表A的由奇异值组成的左奇异向量矩阵；$V$代表A的右奇异向量矩阵。

求A的$U,\sum ,V$.

1. 计算$A^{T}A$
   $$A^{T}A=\left[\begin{array}{cc}2& 0\\ 3& 2\end{array}\right]\left[\begin{array}{cc}2& 3\\ 0& 2\end{array}\right]=\left[\begin{array}{cc}13& 6\\ 6& 4\end{array}\right]$$
2. 计算$A^{T}A$的奇异值$\sigma$
   $$\begin{gathered} {\sigma }_1^2{\sigma }_2^2=det{A}^{T}A=16 \\ {\sigma }_1^2+{\sigma }_2^2=tr{A}^{T}A=17 \\ \therefore {\sigma }_1^2=16,{\sigma }_2^2=1 \\ \therefore {\sigma }_1=4,{\sigma }_2=1 \\ \therefore \Sigma =\left[\begin{array}{cc}4& 0\\ 0& 1\end{array}\right] \end{gathered}$$
3. 将${\sigma }_1,{\sigma }_2$带入$A^{T}A$中求其特征向量
   $$\begin{gathered} {v}_1=\left[\begin{array}{c}\frac{1}{\sqrt{5}}\\ \\ \frac{2}{\sqrt{5}}\end{array}\right],v_2=\left[\begin{array}{c}-\frac{2}{\sqrt{5}}\\ \\ \frac{1}{\sqrt{5}}\end{array}\right] \\ \therefore V=\left[\begin{array}{cc}\frac{1}{\sqrt{5}}& -\frac{2}{\sqrt{5}}\\ & \\ \frac{2}{\sqrt{5}}& \frac{1}{\sqrt{5}}\end{array}\right] \end{gathered}$$
4. 构造标准正交向量
   $$\begin{gathered} u_i=\frac{1}{{\sigma }_i}A{v}_i \\ \therefore u_1=\frac{1}{{\sigma }_1}A{v}_1=\frac{1}{4}\left[\begin{array}{cc}2& 3\\ & \\ 0& 2\end{array}\right]\left[\begin{array}{c}\frac{1}{\sqrt{5}}\\ \\ \frac{2}{\sqrt{5}}\end{array}\right]=\left[\begin{array}{c}\frac{2}{\sqrt{5}}\\ \\ \frac{1}{\sqrt{5}}\end{array}\right] \\ \therefore u_2=\frac{1}{{\sigma }_2}A{v}_2=\frac{1}{1}\left[\begin{array}{cc}2& 3\\ & \\ 0& 2\end{array}\right]\left[\begin{array}{c}-\frac{2}{\sqrt{5}}\\ \\ \frac{1}{\sqrt{5}}\end{array}\right]=\left[\begin{array}{c}-\frac{1}{\sqrt{5}}\\ \\ \frac{2}{\sqrt{5}}\end{array}\right] \\ \therefore U=(u_1,u_2)=\left[\begin{array}{cc}\frac{2}{\sqrt{5}}& -\frac{1}{\sqrt{5}}\\ & \\ \frac{1}{\sqrt{5}}& \frac{2}{\sqrt{5}}\end{array}\right] \end{gathered}$$
5. 写出表达式
   $$A=U\Sigma V^T=\left[\begin{array}{cc}\frac{2}{\sqrt{5}}& -\frac{1}{\sqrt{5}}\\ & \\ \frac{1}{\sqrt{5}}& \frac{2}{\sqrt{5}}\end{array}\right]\left[\begin{array}{cc}4& 0\\ & \\ 0& 1\end{array}\right]\left[\begin{array}{cc}\frac{1}{\sqrt{5}}& \frac{2}{\sqrt{5}}\\ & \\ -\frac{2}{\sqrt{5}}& \frac{1}{\sqrt{5}}\end{array}\right]$$

---

利用奇异值分解（SVD）进行图片压缩

首先我们先找一张图片来进行实验。

通道分离

对于JPG格式的彩色图片，拥有3个颜色通道，R(红)、G(绿)、B(蓝)，那么可以尝试将每个颜色通道进行分离，产生3个形状均为图像高 x 宽 的单通道剧展，即imageR，imageG，imageB。

进行通道分离，将imageArray数组中的每个通道分别单独取出来，得到3个高 $\times$ 宽的二维数组。这3个二维数组中每个位置上的取值就是对应像素的某个颜色通道的取值，代码如下：

import numpy as np
from PIL import ImageoriginalImage = Image.open(r'teriri.jpg', 'r')
imageArray = np.array(originalImage)
R = imageArray[:, :, 0]
G = imageArray[:, :, 1]
B = imageArray[:, :, 2]
print(R)
print(G)
print(B)

运行结果如下：

[[207 207 207 … 141 141 141]
[207 207 207 … 141 141 141]
[207 207 207 … 141 141 141]
…
[246 247 248 … 239 239 239]
[246 247 248 … 239 239 239]
[246 247 248 … 239 239 239]]
[[198 198 198 … 126 126 126]
[198 198 198 … 126 126 126]
[198 198 198 … 126 126 126]
…
[233 234 235 … 235 235 235]
[233 234 235 … 235 235 235]
[233 234 235 … 235 235 235]]
[[215 215 215 … 149 147 147]
[215 215 215 … 149 147 147]
[215 215 215 … 149 147 147]
…
[230 231 233 … 203 203 203]
[230 231 233 … 203 203 203]
[230 231 233 … 203 203 203]]

至此，我们成功得到了3个二维ndarray数组，将R、G、B三个通道成功进行了分离。

矩阵压缩

对每个单通道矩阵进行奇异值分解，按照压缩的实际需要取前k个奇异值，进行3个单通道的矩阵的压缩，最后分别形成3个压缩后的矩阵：imageRC，imageGC，imageBC，代码如下：

def imgCompress(channel,percent):U,sigma,V_T = np.linalg.svd(channel)m = U.shape[0]n = V_T.shape[0]reChannel = np.zeros((m,n))for k in range (len(sigma)):reChannel = reChannel + sigma[k] * np.dot(U[:,k].reshape(m,1),V_T[k,:].reshape(1,n))if float(k) / len(sigma) > percent:reChannel[reChannel < 0] = 0reChannel[reChannel > 255] = 255breakreturn np.rint(reChannel).astype("unit8")

图像重建

将经过奇异值分解处理的3个单通道矩阵合并，从而重构出压缩后的彩色图像。

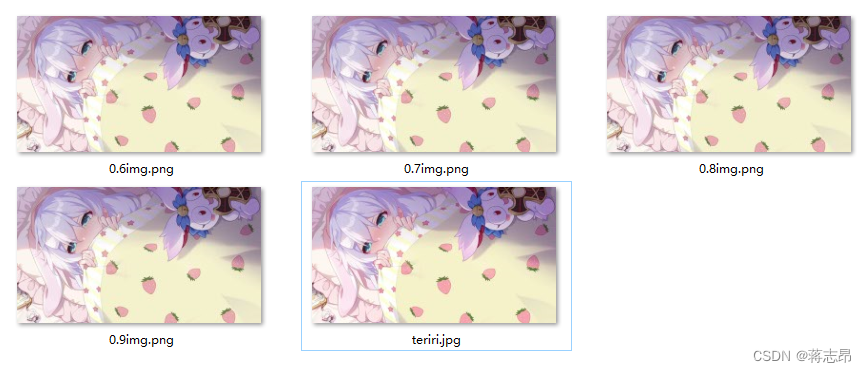
    for p in [0.001, 0.005, 0.01, 0.02, 0.03, 0.04, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]:#p表示取所有奇异值的前多少比例reR = imgCompress(R,p)reG = imgCompress(G,p)reB = imgCompress(B,p)reI = np.stack((reR,reG,reB),2)Image.fromarray(reI).save("{}".format(p)+"img.png")

整体运行结果如下：

比例为0.001至0.04
>0.05至0.5

0.6至原图

总结：

1. 取前0.1%奇异值重建的图像是一个非常模糊的，基本只能看到大体轮廓。
2. 取前1%奇异值重建的图像就可以看到一个比较清晰的图片了。
3. 随着比例的提升，图片越来越清晰，到30%的时候就基本与原图一致了。