题目描述

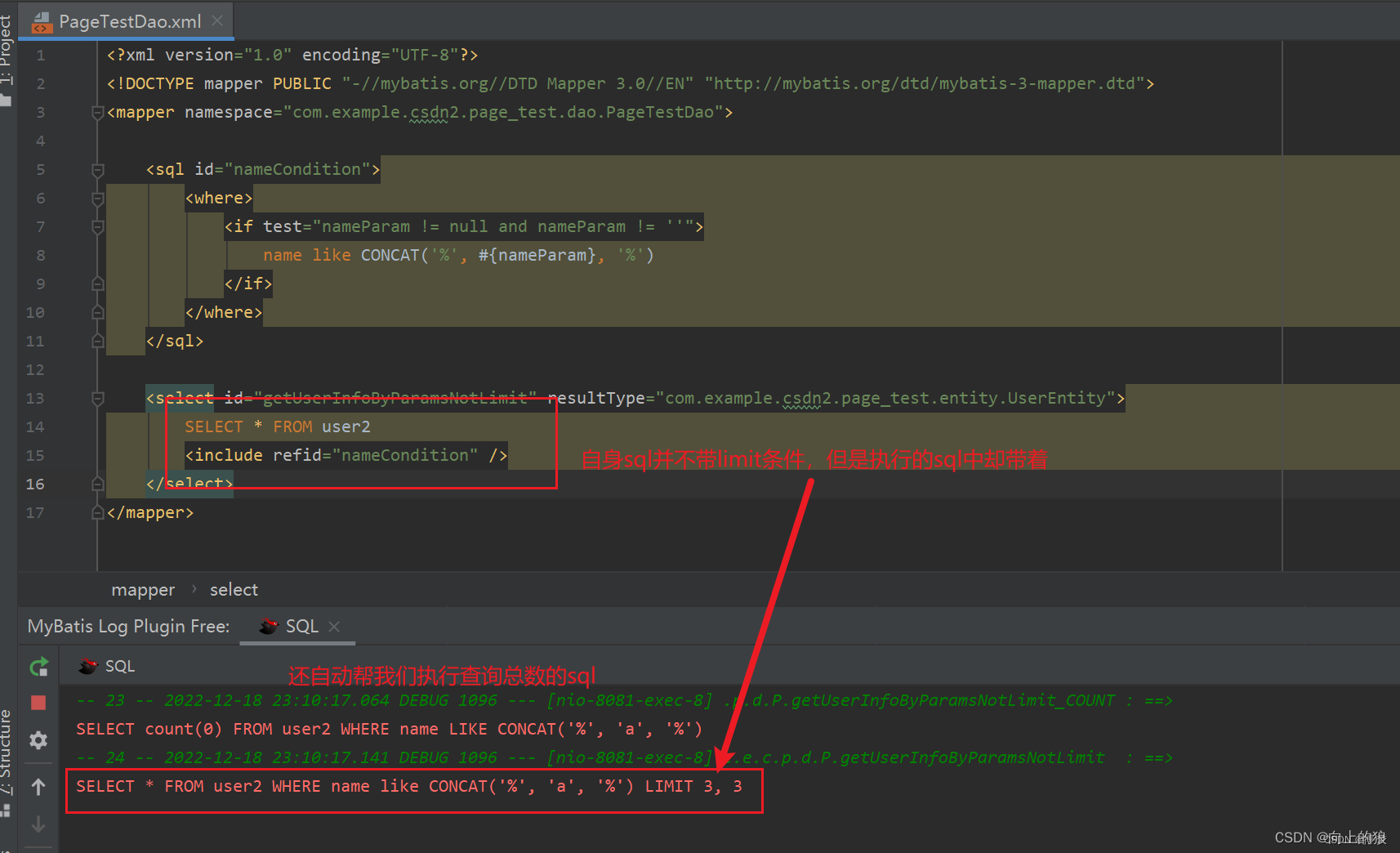
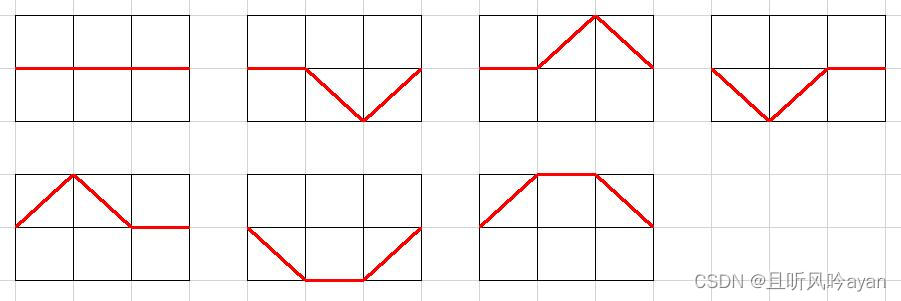
一个n列的网格，从(0,0)网格点出发，波形存在平波(从(x,y)到(x+1,y))，上升波(从(x,y)到(x+1,y+1))，下降波(从(x,y)到(x+1,y−1))三种波形，请问从(0,0)出发，最终到达(n,0)的不同波形有多少种？如图，3列网格有7种不同的波形。

输入

第一行是样例数T(1≤T≤42)。 以后每行一个整数n(1≤n≤42)。

输出

每行输出一个样例的结果。

样例输入

3
1
2
3

样例输出

1
3
7

AC代码

#include<stdio.h>
long long f[45][45]={};
void init(){f[1][21]=1;f[1][22]=1;f[1][23]=1;int i,j;for(i=2;i<=43;i++){for(j=1;j<=43;j++){f[i][j]=f[i-1][j-1]+f[i-1][j]+f[i-1][j+1];}}
}
int main(){int T;scanf("%d",&T);init();while(T--){int n;scanf("%d",&n);printf("%I64d\n",f[n][22]);}
}

利用递推解题，规律：f[i][j]=f[i-1][j-1]+f[i-1][j]+f[i-1][j+1]。与1354机器人那道题相似。