目录
一. SIS问题的困难性
二. SIS问题归约的性质
2.1 2004年 [MR04]
2.2 2008年 【GPV08】
2.3 2013年【MP13】
三. 归约证明
3.1 核心理解
3.2 归约步骤
3.3 性质理解
一. SIS问题的困难性
推荐先阅读:
格密码基础:SIS问题的定义与理解-CSDN博客
借鉴1996年Ajtai的工作,大量的工作开始研究最坏情况下的SIS问题的困难性。SIS问题中一共有四个参数,需要满足如下:
如果能以不可忽略的概率解决SIS问题,那么就可以在随机的n维格上,解决近似GapSVP和SIVP问题。此处的近似因子取值为:
GapSVP:decisional approximate shortest vector problem,判定性近似最短向量问题
SIVP: approximate shortest indenpendent vectors problem
需要注意的是m和q的值会极大影响SIS问题的困难性,而且根据归约准则,当范数上限值越大时,GapSVP和SIVP问题的近似因子也会变大。整个多项式时间复杂度的归约分成两步:
- 假设存在一个oracle可以解决SIS问题
- 利用此oracle尝试在任意n维格上解决近似的GapSVP和SIVP问题
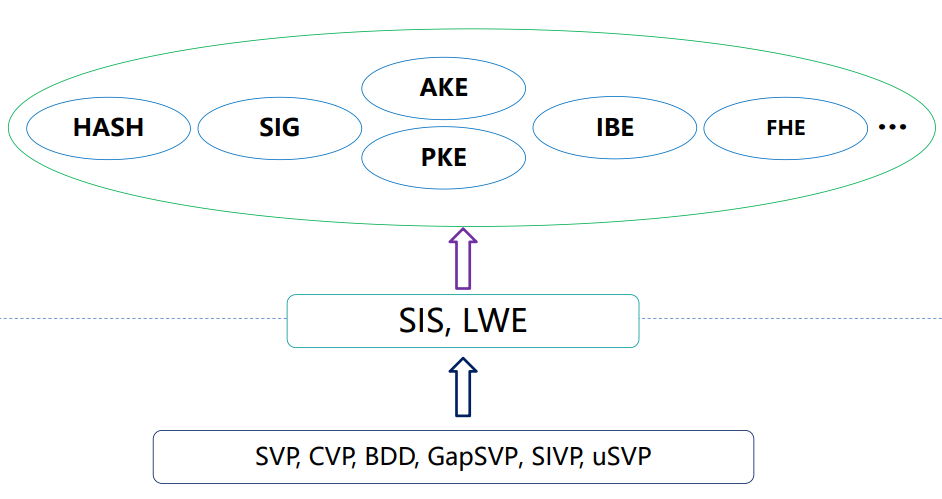
二. SIS问题归约的性质
理论上,我们希望归约时的模q和近似因子(approximation factor)越小越好,因为这样可以产生更小的实例(instance)和密码学的公私钥,以及更强的网络安全性保证。接下来,我们来看几个SIS问题归约时重要的发展历程:
2.1 2004年 [MR04]
在2004年,Micciancio 和 Regev引入了格上高斯分布和调和分析(harmonic analysis),从而导出了格密码中重要的概念,叫做光滑参数(smoothing parameter),写做:
如果在格点周围外加一个噪声,该噪声分布服从高斯分布。当分布的方差大于格的光滑参数时,离散的格点就可以变成连续的均匀分布。对于光滑参数有一种直观的形式化语言,如下:
The amount of Gaussian error needed to “smooth out” the discrete structure of a lattice.
借助此理论便可以产生均匀且随机的SIS实例,从而对任意输入的格均满足推论。在此论文中,近似因子的取值为:
当选择合适的值时,近似因子可取:
此时模q可取:
可以看到以上两者的取值都相对较小。
2.2 2008年 【GPV08】
在2008年,Gentry, Peikert 和Vaikuntanathan将模数q的值优化到:
此时的近似因子与2004年的工作类似:
此论文创新性提出了离散高斯分布(discrete Gaussian),待会我们会简单分析此理论。
2.3 2013年【MP13】
在2013年,Micciancio 和 Peikert将模数q优化到:
其中为大于0的常数。
如果把看成固定的常数的话,此时的q已经是最优的了。因为SIS问题中,总存在平凡解就是q。
借助卷积引理(convolution lemma),在利用SIS的oracle进行归约时,此理论需要使用到范数,而不是常规的
范数。
三. 归约证明
SIS问题的困难性涉及到最坏情况和平均情况(worst case/average case)的归约证明。该归约的思路:给定任意n维格L的格基B,已知一个平均情况的SIS的oracle,目标是解决SIVP问题。
在这里简单解释下近似的SIVP问题:
给定近似因子,尝试找出n个线性独立的格向量,它们的长度都小于:
3.1 核心理解
首先输入格基B,从此格中随机选择一部分独立的格向量S,也就是:
将此处的S看成一个矩阵。接着利用SIS oracle不断对该矩阵进行归约运算,使其长度至少缩短一半以上,也就是:
备注:此处矩阵的长度代表其中最长向量的长度,也就是:
不断迭代重复,直到最终的结果符合SIVP问题的要求。
3.2 归约步骤
第一步:取样
借助格L上的离散高斯分布,采样出m个随机的格点,形成集合S,也就是:
这些初始向量不会太长。接着将这m个向量形成矩阵V

第二步:形成SIS oracle的输入
运算得到:
重复运算m次,由此可得:
需要注意的是,因为是格点,所以
一定是整数的。
接着从此时的矩阵A输入到SIS的oracle中。
第三步:运算
SIS的oracle会输出一个解,也就是:
那么可得:
很明显发现此时的向量长度在变小。

3.3 性质理解
(1)SIS oracle分析
根据以上归约过程,给定一个矩阵A,z为其SIS问题的答案。因为是格点,所以可得:
由此可运算:
![]()
所以可得以下运算出的v为L格点:
SIS求解出的z长度是有上限的,也就是:
在产生向量v时,使其满足:
两者结合可得:
当我们选择模数q如下:
即可以得到:
第一轮迭代完成。
(2)矩阵A均匀分布
借助光滑参数,在一定条件下均匀分布:
也就是:
此处说明v在模qL上为均匀分布,再根据:
B是确定的,也就是a和v之间是双射运算,所以可得矩阵A也是均匀分布(严格来讲应该是跟均匀分布不可区分)。