回顾递归的快速排序,都是先找到key中间值,然后递归左区间,右区间。
那么是否可以实现非递归的快排呢?答案是对的,这里需要借助数据结构的栈。将右区间左区间压栈(后进先出),然后取出左区间,再将左区间的子右区间和子左区间压栈,再取出左区间的子左区间......,当栈为空时,即全部取出,此时已经有序。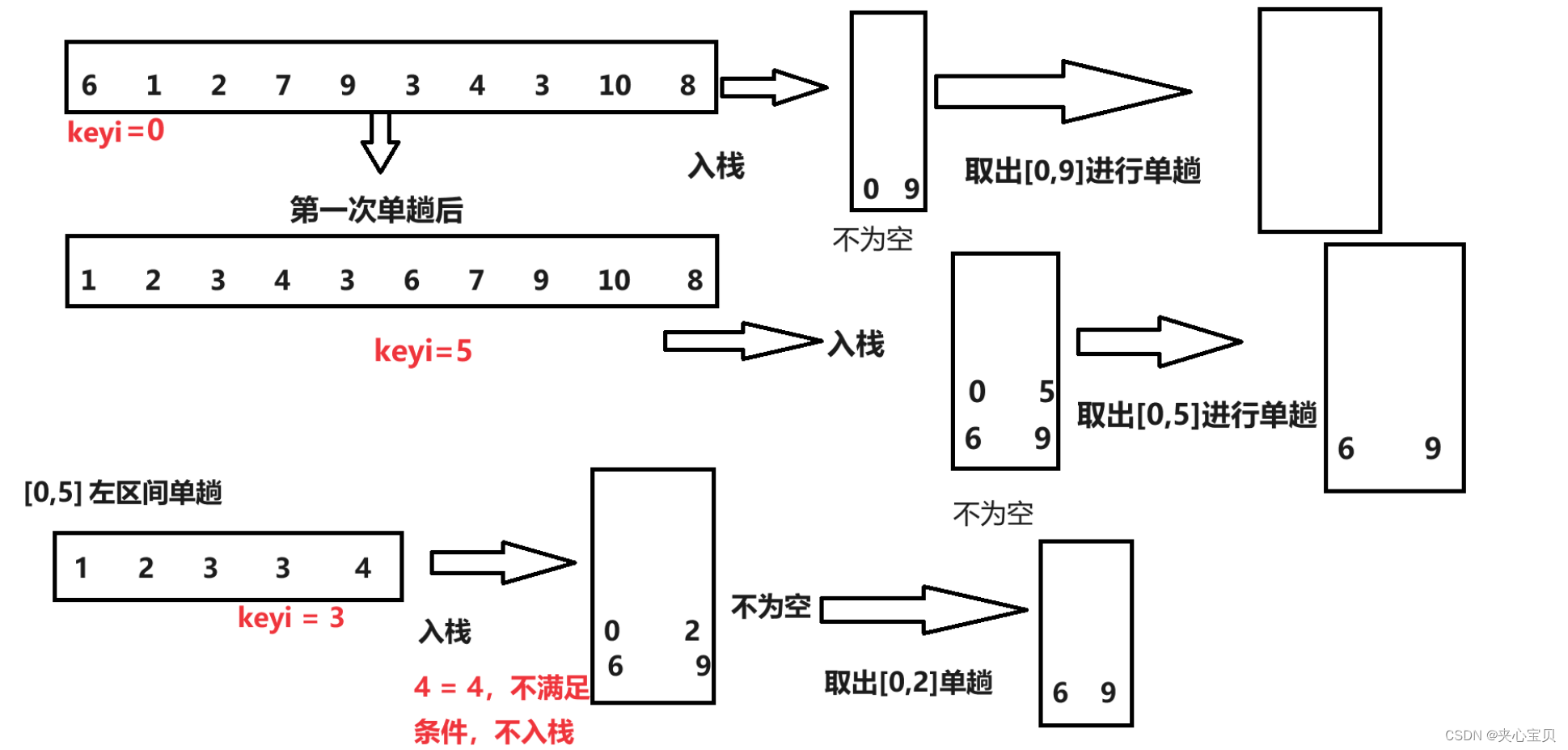

和递归一样,首先用三数取中来优化:
//三数取中
int GetMidi(int* arr, int begin, int end)
{int midi = (begin + end) / 2;if ((arr[begin] > arr[midi] && arr[begin] < arr[end])|| (arr[begin]) > arr[end] && arr[begin] < arr[midi])midi = begin;if ((arr[end] > arr[midi] && arr[end] < arr[begin])|| (arr[end]) > arr[begin] && arr[end] < arr[midi])midi = end;return midi;
}接着借用递归快排的指针法,来进行单趟排序,得到中间基准值,并划分做右区间(不记得指针法的回看博客)
int QuickSort_pointer_incline(int* arr, int begin, int end)
{int midi = GetMidi(arr, begin, end);Swap(&arr[begin], &arr[midi]);int keyi = begin;int prev = begin, cur = prev + 1;while (cur <= end){if (arr[cur] < arr[keyi] && ++prev != cur)Swap(&arr[prev], &arr[cur]);++cur;}Swap(&arr[prev], &arr[keyi]);keyi = prev;return keyi;
}最后使用栈来压栈出栈
void QuickSort_NonR_incline(int* arr, int begin, int end)
{ST s;STInit(&s);//放入端点//因为后进先出,所以先入右,后入左,区间[左,右]STPush(&s, end);STPush(&s, begin);while (!STEmpyty(&s)){//出栈int left = STTop(&s);STPop(&s);int right = STTop(&s);STPop(&s);//指针单趟排序int keyi = QuickSort_pointer_incline(arr, left, right);//[left,keyi-1],keyi,[keyi+1,right]//入右区间,同样先入右区间的右端点,再左端点if (keyi + 1 < right){STPush(&s, right);STPush(&s, keyi + 1);}//入左区间,同样先入左区间的右端点,再左端点if (left < keyi - 1){STPush(&s, keyi - 1);STPush(&s, left);}//循环回去,又取出区间,再次单趟排序后,又入子右区间,子左区间}STDestroy(&s);
}