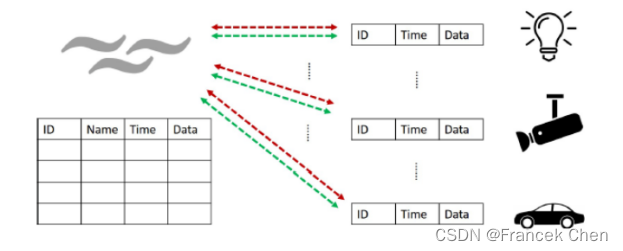
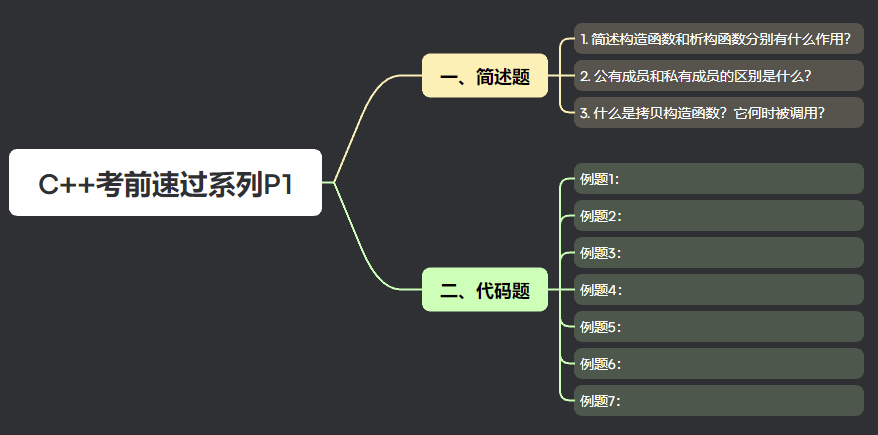
1.集合

1.集合的概念（意思）

把集合理解成一个塑料袋

要往塑料袋装什么，

装的元素就是里面装的各个东西，

表示方法

1。直接穷举

A={装的到底是什么（竹子）}

2.描述法

描述装的东西的性质，进而去限制装的到底是什么

A={X|X是棍状的；X是什么颜色的；X是什么材料的} 

装的元素数量是无限的

N,R,Z,Q

N是自然数，整数，（包括0），非负，0，1，

Z是……整数集（合），正的负的零都可以

Q是……有理数集（合），怎么判断是不是有理数，就是看这个数能不能被表示成两个整数相除，方法。。。如果说一个数能被表示成分数的形式，那么就是有理数，

为什么？整数都是有理数，？整数A/1=整数A

0.999999（无穷循环），？是有理数，（1/3）*3，（3/3）

0.33333（无穷循环），有理数？是

R是…实数集（合），R里既包含有理数也包含无理数

什么是实数？实数就是有理数和无理数的并集合

实数是一个很大的范围，高中的所有范围基本上都是实数

N，Z,Q，R

N<Z<Q<R

购物的大袋子A，小于三十块钱的袋子B，小于十块钱的袋子C，

C里的一定在B里，B,C也一定都在A里

在B里一定在C里吗？

C<B，

同一个元素会不会在多个集合里，1在N,Z,Q,R

数能被表示成分数，那就是有理数

分数的分子分母都是整数

49/17，是有理数

2.2/1.3

什么是无理数？无法用分数表示的数，都是无理数

怎么描述无理数，

根式，根号二，能被表示成分数……？

提出根式是为什么呢？就是因为有一些数是无法用分数来表示的，

根式，根2，根3，根5，就是最简的形式，没有转化成分数的形式

整数-》小数（有限的，除法能除尽的）-》小数，分数（不能除尽的，无限，有循环）-》小数，不能被除法（分子分母都是整数）所表示的（是无限不循环的，圆周率，自然底数）

怎么产生这个小数？勾股定理，a^2+b^2=c^2（一般是等式右侧产生无理数）

幂的存在，因为有幂的存在，二次幂是自己和自己相乘

等式左侧，这个加号，加减乘除结合在一起

c^2=2=c*c,c=2/c，并不能被表示成分子分母都是整数的分数

用什么方式去表示？就是用根式去表示这类数，就是开方

乘除，都不涉及加减，分式上都是同乘同除

1=1/1=2/2=3/3=4/4=……，1是有理数

由除法产生的数是不是都是有理数？是的

why

所谓分数，其实就是除式的一个表示，3/7，分数的形式，上面一个数，一个杠（除以），下面一个数，

是不是所有分数都能写成除法的形式？能的

上面的数除以下面的数，这就是分数的意思

x/y=x➗y

有除法，就一定可以表示为分数，这个➗就相当于分数的/
 

能被分数所表示的数，且满足分子分母都是整数的数，就是有理数

不能被这样表示的数，是无理数

7.7/3/3-》77/33，可以经过经过转化变为上面说的形式

所有分数都是有理数？反例……1/根号二，根号二=根号二/1

分数的分子分母不能是无理数，有一个是的话，就有可能不是有理数

分数的分子分母都是有理数，那么分数一定是有理数？

如果是有理数，那么一定可以转化为整数相除的形式

分数的分子分母都是无理数，那么分数一定是无理数？

否，反例……根号2/根号2=1，根号8/根号2=2

符号

E，念作“属于” 

0∈A ，10不属于A

东西属于塑料袋，用E表示属于，E打个斜杠不属于

牙膏属于塑料袋，牙膏∈集合A

类似于用=去描述等于 ，画一个斜杠就是不等于号

1.塑料袋里装的就是国家， 

 2.不在就是不属于，就填第二个符号

3.十字相乘法

4.

总结一下，明确集合的概念，

就是要知道集合里装的是什么，1里面装的是国家，234里装的就是一个一个的数字

塑料袋里装的，还是塑料袋

外面的大塑料袋，它的元素是什么？

最外层的集合，里面的元素，小集合

大塑料袋={小塑料袋，商品}

集合就是拿一个塑料袋把你要装的东西都装起来，这个就叫集合

它是一个抽象的概念，它只是说用一个统一的范围来表述满足某一些条件的东西

元素（塑料袋里的东西）的性质 

1.无序性

塑料袋，

A=1，2，3

B=2，3，1 

A=B

2.不重复性

A=1,1,2,3，A不表示集合

2.集合的基本关系

运算，集合的运算

什么是集合的运算，什么是运算？运算包含运算元素与运算符，

加减乘除是运算，二元，一元；运算元素是数字，一个一个的数字，运算符是加减乘除

A+B,

交并补，

交运算，