导语

之前平衡二叉树讲解中，可以了解到AVL在插入或删除频繁的场景，需要消耗大量的时间来调整，使树重新满足平衡条件。红黑树就此作出优化，在查询速率和平衡调整中寻找平衡，放宽了树的平衡条件，从而可以用于 增加删除 频繁的场景。

---

一、红黑树的基本概念

1、红黑树的定义

红黑树（Red Black Tree）是一颗自平衡（self-balancing）的二叉排序树（BST）。

【注意，这里的自平衡和平衡二叉树AVL的高度平衡不同】

在红黑树中，节点被标记为红色和黑色两种颜色。

树上的每一个结点都遵循下面的规则：

• 特性1：节点非黑即红

• 特性2：根节点一定是黑色

• 特性3：叶子节点（NULL）一定是黑色

• 特性4：每个红色节点的两个子节点都为黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

• 特性5：从任一节点到其每个叶子的所有路径，都包含相同数目的黑色节点。【平衡特征】

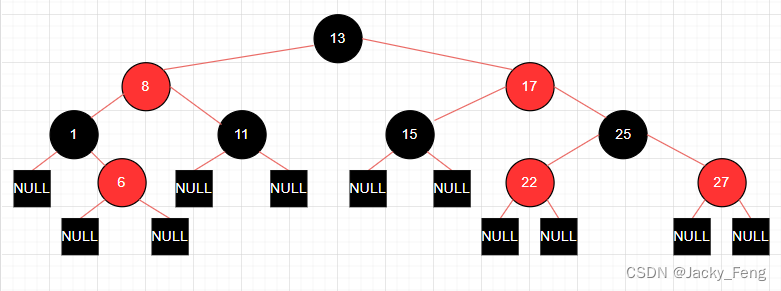
如果一个结点没有子结点或父结点，则该结点相应属性值为NULL。

这些NULL被视为指向二叉搜索树的叶结点（外部结点）的指针，而把带关键字的结点视为树的内部结点。

为了便于处理红黑树代码中的边界条件，使用一个NULL来代表所有的NIL：所有的叶结点和根结点的父结点。

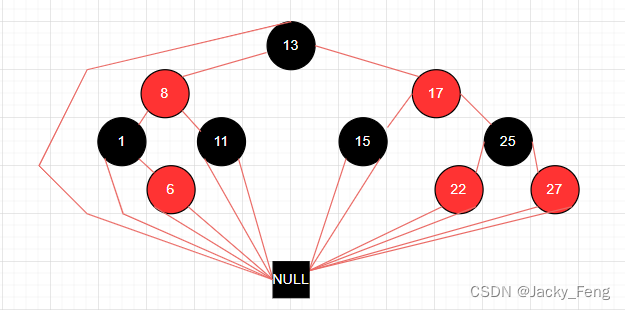
 红黑树并不一定是一棵AVL平衡二叉搜索树。

 如上图，这个树是一棵红黑树，但是不是一棵AVL平衡二叉树。

红黑树的特性5，从任一节点到其每个叶子的所有路径，都包含相同数目的黑色节点， 说明：

红黑树的 左子树和右子树的黑节点的层数是相等的

红黑树的平衡条件，不是以整体的高度来约束的，而是以黑色节点的 高度 来约束的。

所以称红黑树这种平衡为黑色完美平衡。

 结点的黑高（bh）:从某结点出发（不含该结点）到达任一空叶结点的路径上黑结点总数。

二、红黑树的存储结构

对于红黑树，首先是二叉搜索树，所以会有 左右孩子指针 和 数据域，然后特殊之处是每个结点都有颜色，所以需要加一个 颜色标记（Red or Black）。

enum Color {Red,Black
};struct RBNode {struct RBNode* parent;struct RBNode* left;struct RBNode* right;int data;Color color;RBNode(int val) :parent(nullptr), left(nullptr), right(nullptr), data(val),color(Red) {}
};

【为什么创建结点时默认结点颜色为红色？】

红色在父结点（如果存在）为黑色结点时，红黑树的黑色平衡没被破坏，不需要做自平衡操作。但如果插入结点是黑色，那么插入位置所在的子树黑色结点总是多1，必须做自平衡。

三、自平衡操作

1、左旋

以某个结点作为支点(旋转结点)，其右子结点变为旋转结点的父结点，右子结点的左子结点变为旋转结点的右子结点，左子结点保持不变。

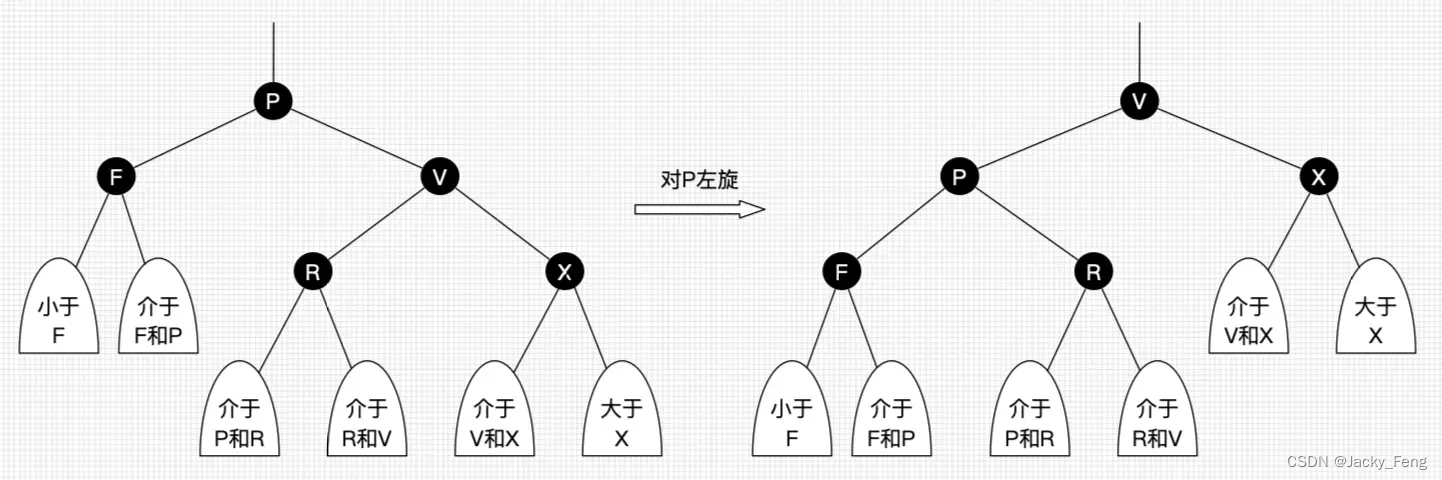
 2、右旋

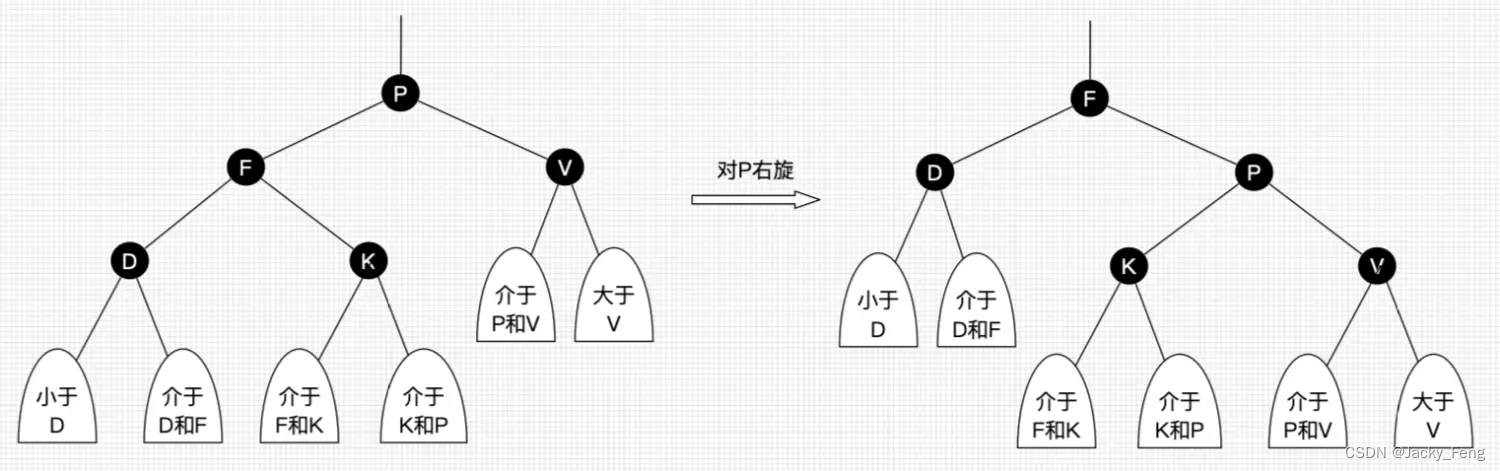
以某个结点作为支点(旋转结点)，其左子结点变为旋转结点的父结点，左子结点的右子结点变为旋转结点的左子结点，右子结点保持不变。

3、变色

 结点的颜色由红变黑或由黑变红。

四、红黑树的基本操作

1、查找

对于要查找的数据 data，从根结点出发，每次选择左子树或者右子树进行查找，总共四种情况依次进行判断：

1）若为空树，直接返回 false；

2） data 小于 树根结点的数据域，说明 data 对应的结点不在根结点，也不在右子树上，则递归返回左子树的 查找 结果；

3） data 大于 树根结点的数据域，说明 data 对应的结点不在根结点，也不在左子树上，则递归返回右子树的 查找 结果；

4） data 等于 树根结点的数据域，则直接返回 true ；

bool RBTreeFind(RBNode* T, int data) {if (T == nullptr) {return false;                        // 空树}if (data < T->val) {return RBTreeFind(T->left, data);       // data<val，递归查找左子树}else if (data > T->val) {    return RBTreeFind(T->right, data);      //  data>val，递归查找右子树}return true;                             //  data=val
}

2、插入

（1）原理分析

和AVL平衡二叉树类似，红黑树的插入首先需要找到合适的插入位置，特殊的的是插入过程需要为新元素染色且需要重新平衡。

对于要插入的数据 data ，从根结点出发，分情况依次判断：

【情景1】：红黑树为空树。 【处理】把插入结点作为根结点，并把结点由红色变为黑色。

【情景2】：插入结点数据data已存在。 【处理】无须执行插入，直接返回。（若是key-value结构，需要更新当前结点的值为插入结点的值）

【情景3】：插入结点的父结点为黑色结点。 【处理】：直接插入。

【情景4】：插入结点的父结点为红色结点。

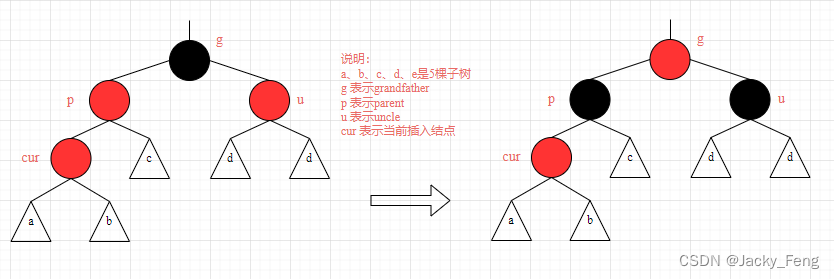
【情景4-1】：叔叔结点存在并且为红结点。

【处理】：① 将P（父亲结点）和U（叔叔结点）设置为黑色

                  ② 将G（祖父结点）设置为红色

                  ③ 将G 设置为当前插入结点

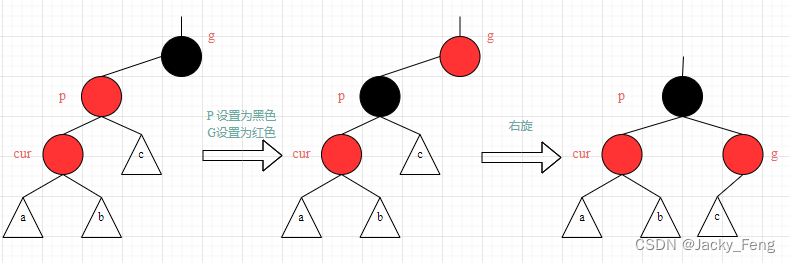
【情景4-2】：叔叔结点不存在或者为黑结点，并且插入结点的父亲结点是祖父结点的左孩子结点。 

【情景4-2-1】插入结点是其父结点的左子结点

【处理】：① 将 P 设置为黑色

                  ② 将 G 设置为红色

                  ③ 以 P 为支点，对 G 进行右旋

 【情景4-2-2】插入结点是其父结点的右子结点

 【 处理】：① 对 P 进行左旋

                    ② 把 P 设置为插入结点

                    ③ 进行情景4-2-1处理

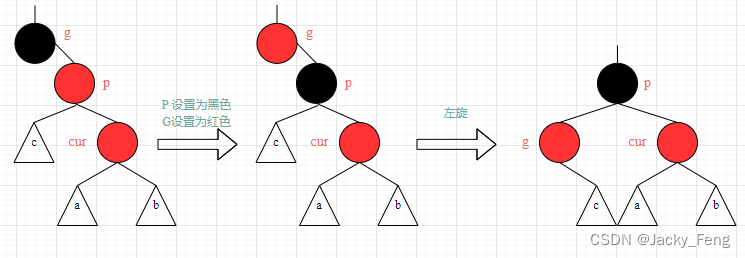
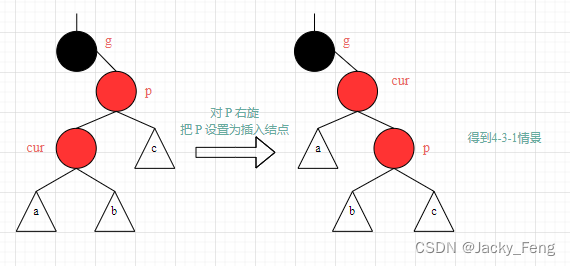
【情景4-3】：叔叔结点不存在或者为黑结点，并且插入结点的父亲结点是祖父结点的右孩子结点。 

【情景4-3-1】插入结点是其父结点的右子结点

【处理】：① 将 P 设置为黑色

                  ② 将 G 设置为红色

                  ③ 以 P为支点，对 G 进行左旋

【情景4-3-2】插入结点是其父结点的左子结点

【处理】：① 对 P 进行右旋

                  ② 将 P 设置为插入结点，得到情景4-3-1

                  ③ 进行情景4-3-1的处理

 

（2）代码实现

（后续补充）

3、删除

（1）原理分析

红黑树的删除操作和AVL树的删除操作类似，也包括两部分工作：① 查找目标结点；② 删除后自平衡。

查找目标结点流程和查找操作是一致的，结果主要有两种情况：① 当不存在目标结点时，忽略本次操作； ② 当存在目标结点时，删除后就得做自平衡处理了。删除结点后我们还需要找结点来替代删除结点的位置，不然子树跟父辈结点断开了，除非删除结点刚好没子结点，那么就不需要替代。

【注意】实际进行删除操作时，并不会先进行删除目标结点，再用替代结点连接，这样实际使得过程更加复杂（①释放目标空间；②替代结点重新连接目标空间的父结点和左右子结点；③断开替代结点原连接；④断开目标结点连接）。

实际删除操作是：①找到替代结点，用替代结点的值替换目标结点值；②释放替代结点空间；③断开替代结点连接。

二叉树删除操作找替代结点有3种情情景：

• 情景1：若删除叶子结点（非NIL结点）

        ① 如果为红色，直接删除即可，不影响黑高值

        ② 如果为黑色，导致黑高失衡，需要平衡调整

• 情景2：若删除结点只有一个子结点（只有左子树或右子树）

       删除结点只能是黑色，其子结点为红色，否则无法满足红黑树性质。

       处理方法：将红色子结点值拷贝到父结点，实际删除结点操作为删除红色子结点。

• 情景3：若删除结点有两个子结点

       使用删除结点的前驱或后继结点作为删除的替代结点，转换为情景1或情景2

上述分析过程可以参考下图示例： 

 

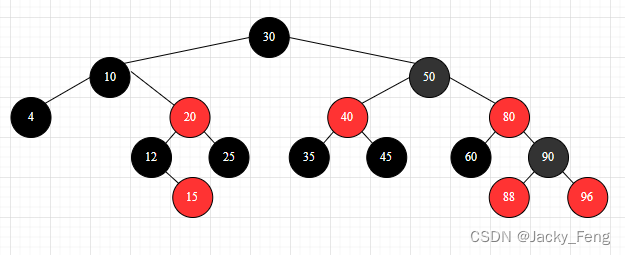
删除黑色结点调整情况：

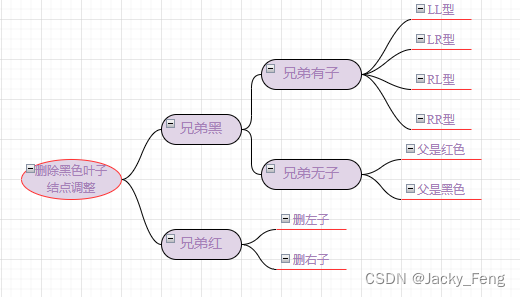
旋转类型定义： 

看兄弟结点（黑色）及其红色结点位置。

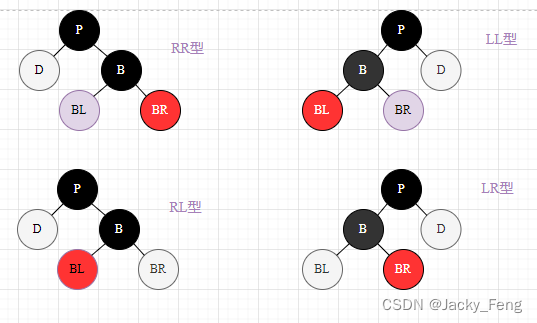
平衡情景综合分析：
【情景1】：删除结点是一个黑色根结点（只有一个根结点）。【处理】：直接删除。
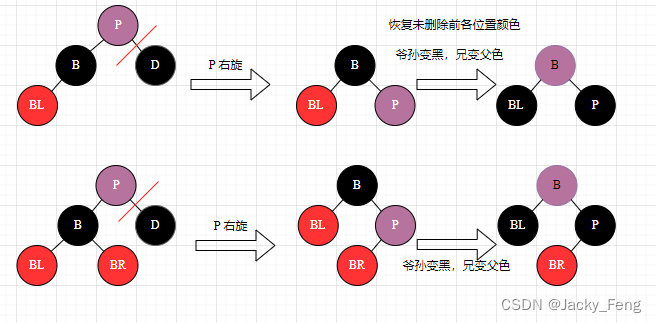
【情景2-1】：删除结点是黑色叶子结点，兄弟为黑色，兄弟有红色子结点

(1)  LL 型   【处理】：右旋 + 爷孙变黑，兄变父色

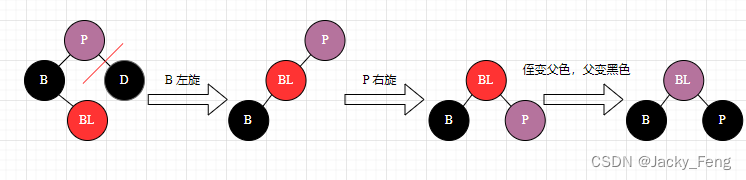
（2）LR 型  【处理】：左旋 + 右旋 +侄变父色，父变黑色

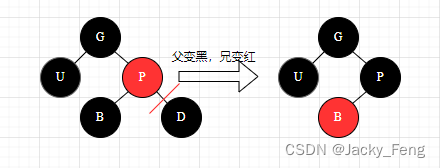
【情景2-2-1】：删除结点是黑色叶子结点，兄弟为黑色，兄弟无红色子结点，父结点是红色。

        【处理】：父变黑，兄变红

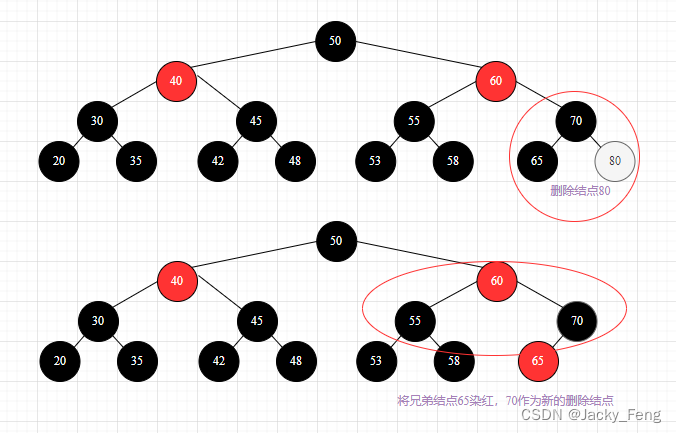
 【情景2-2-2】：删除结点是黑色叶子结点，兄弟为黑色，兄弟无红色子结点，父结点是黑色。

         【处理】：① 把兄弟结点染红；②把父结点当作被新删除结点，递归前面的方法，进行相应                             处理，直至遇到红色父结点并将其染黑，或遇到根结点。

 【情景3】：删除结点是黑色叶子结点，兄弟为红色

         【处理】：兄弟和右侄颜色互换 + 右旋

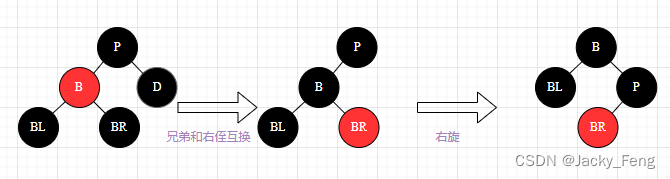
删除结点的步骤：

1.没有找到删除结点，则直接返回。

2.如果删除的是唯一根结点，释放空间并root置空返回；

3.删除叶子结点

4.删除只有一个子结点的节点。

5.删除有两个子结点的节点。

（2）代码实现

 辅助函数：

RBNode* FindTreeNode(int val);//查找删除结点
RBNode* FindProvNode(RBNode* node);//查找前驱结点
RBNode* FindLaterNode(RBNode* node);//查找后继结点

获得替代结点方法：目的是减少调整次数

• 先找前驱，如果找到以下两种情况则返回前驱：①红色叶子结点；②有一个红色叶子结点的黑色结点
• 否则返回后继。

（实现代码后续补充）