一、引言

时间复杂度是衡量算法运行效率的一项重要指标，它描述了随着输入规模的增加，算法的执行时间如何增长。在算法设计与分析中，我们经常面临着优化时间复杂度的任务，以便提高程序的性能。本博客将深入探讨时间复杂度的优化法则，为开发者提供一系列实用的技巧和策略。

1.1 什么是时间复杂度？

时间复杂度是一种用于衡量算法性能的概念，它表示随着输入规模的增加，算法执行所需时间的增长趋势。通常用大O表示法（Big O Notation）来描述时间复杂度。对于一个算法，我们关注的是其运行时间与输入规模之间的关系，而不是具体的执行时间。

1.2 时间复杂度的重要性

优化时间复杂度对于确保程序在大规模数据上的高效性至关重要。随着数据量的增加，时间复杂度较低的算法将表现得更为出色，因此对算法进行合理的时间复杂度分析和优化，能够显著提高程序的性能，减少资源消耗。

1.3 大O表示法简介

大O表示法是一种用于描述算法渐近复杂度（asymptotic complexity）的数学表示方法。它关注算法的运行时间在输入规模无限增长时的增长趋势。在大O表示法中，我们主要关注算法执行时间的上界，即最坏情况下的运行时间。

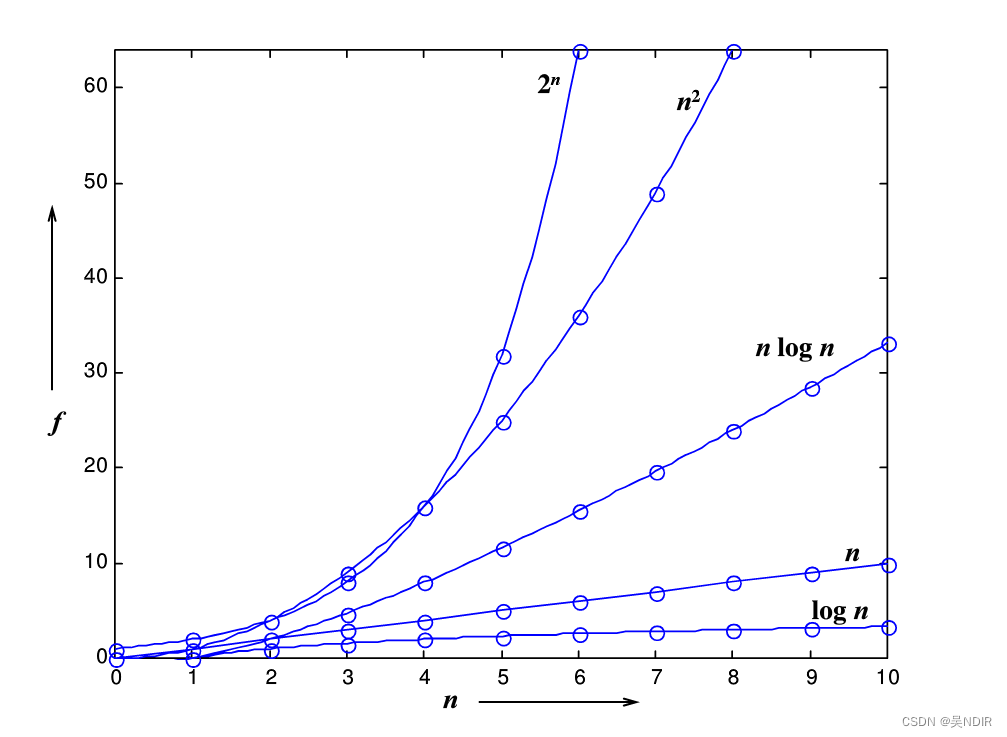
1.4 常见时间复杂度的分类与解释

时间复杂度可以分为常数时间复杂度、对数时间复杂度、线性时间复杂度、平方时间复杂度等多种类型

时间复杂度	描述	示例
O(1)	常数时间复杂度，执行时间是常数	访问数组元素、插入/删除链表节点
O(log n)	对数时间复杂度，执行时间与对数成正比	二分查找、某些分治算法
O(n)	线性时间复杂度，执行时间与输入规模成正比	数组遍历、查找未排序的数组中的元素
O(n log n)	线性对数时间复杂度，常见于排序算法	快速排序、归并排序
O(n^2)	平方时间复杂度，执行时间与输入规模的平方成正比	嵌套循环的简单算法
O(2^n)	指数时间复杂度，执行时间与输入规模的指数成正比	解决某些组合问题的朴素递归算法

了解这些常见时间复杂度的类型对于分析算法性能和进行优化至关重要。

二、实例分析

在这一部分，我们将通过具体的C语言示例来演示时间复杂度的优化法则的应用。

2.1 优化循环结构

考虑以下示例，计算数组中元素的总和：

#include <stdio.h>int sum(int arr[], int n) {int result = 0;for (int i = 0; i < n; i++) {result += arr[i];}return result;
}

优化技巧：

• 避免不必要的循环： 在这个例子中，循环的目的是计算数组元素的总和，没有不必要的循环。

• 减少迭代次数： 这里的循环次数是数组的长度n，是必要的迭代次数。

2.2 选择与优化数据结构

考虑以下示例，查找数组中是否存在某个元素：

#include <stdio.h>int search(int arr[], int n, int target) {for (int i = 0; i < n; i++) {if (arr[i] == target) {return i;}}return -1;
}

优化技巧：

• 选择合适的数据结构： 如果数组是有序的，可以考虑使用二分查找，将时间复杂度从O(n)降低到O(log n)。

2.3 递归算法的优化

考虑以下示例，计算斐波那契数列的第n个数字：

#include <stdio.h>int fibonacci(int n) {if (n <= 1) {return n;}return fibonacci(n - 1) + fibonacci(n - 2);
}

优化技巧：

• 尾递归的利用： 将递归形式转化为尾递归，可以通过循环来实现，提高效率。

• 记忆化搜索： 使用数组等数据结构缓存已经计算过的结果，避免重复计算。

2.4 尾递归的利用

尾递归是一种特殊的递归形式，其中递归调用是函数的最后一个操作。C语言并没有对尾递归进行显式的优化，但我们可以通过重新设计递归函数来模拟尾递归的效果，以减少函数调用栈的深度。

#include <stdio.h>// 非尾递归的阶乘函数
int factorial(int n) {if (n == 0 || n == 1)return 1;elsereturn n * factorial(n - 1);
}// 尾递归的阶乘函数
int tail_factorial(int n, int result) {if (n == 0 || n == 1)return result;elsereturn tail_factorial(n - 1, n * result);
}int main() {int num = 5;printf("Factorial of %d: %d\n", num, factorial(num));printf("Tail-optimized factorial of %d: %d\n", num, tail_factorial(num, 1));return 0;
}

通过使用尾递归优化，我们可以减少函数调用栈的深度，提高算法的性能。

2.5 记忆化搜索

对于一些递归算法，存在大量的重复计算，这时可以使用记忆化搜索（Memoization）来避免重复计算。在C语言中，我们可以利用数组或哈希表来保存已经计算过的结果。

#include <stdio.h>#define MAX_N 100
int memo[MAX_N];// 记忆化搜索的斐波那契数列计算
int fibonacci(int n) {if (n <= 1)return n;if (memo[n] != -1)return memo[n];memo[n] = fibonacci(n - 1) + fibonacci(n - 2);return memo[n];
}int main() {int num = 10;// 初始化memo数组for (int i = 0; i < MAX_N; ++i)memo[i] = -1;printf("Fibonacci of %d: %d\n", num, fibonacci(num));return 0;
}

通过记忆化搜索，我们可以在递归算法中避免重复计算，提高算法的效率。