文章目录
- 优化问题
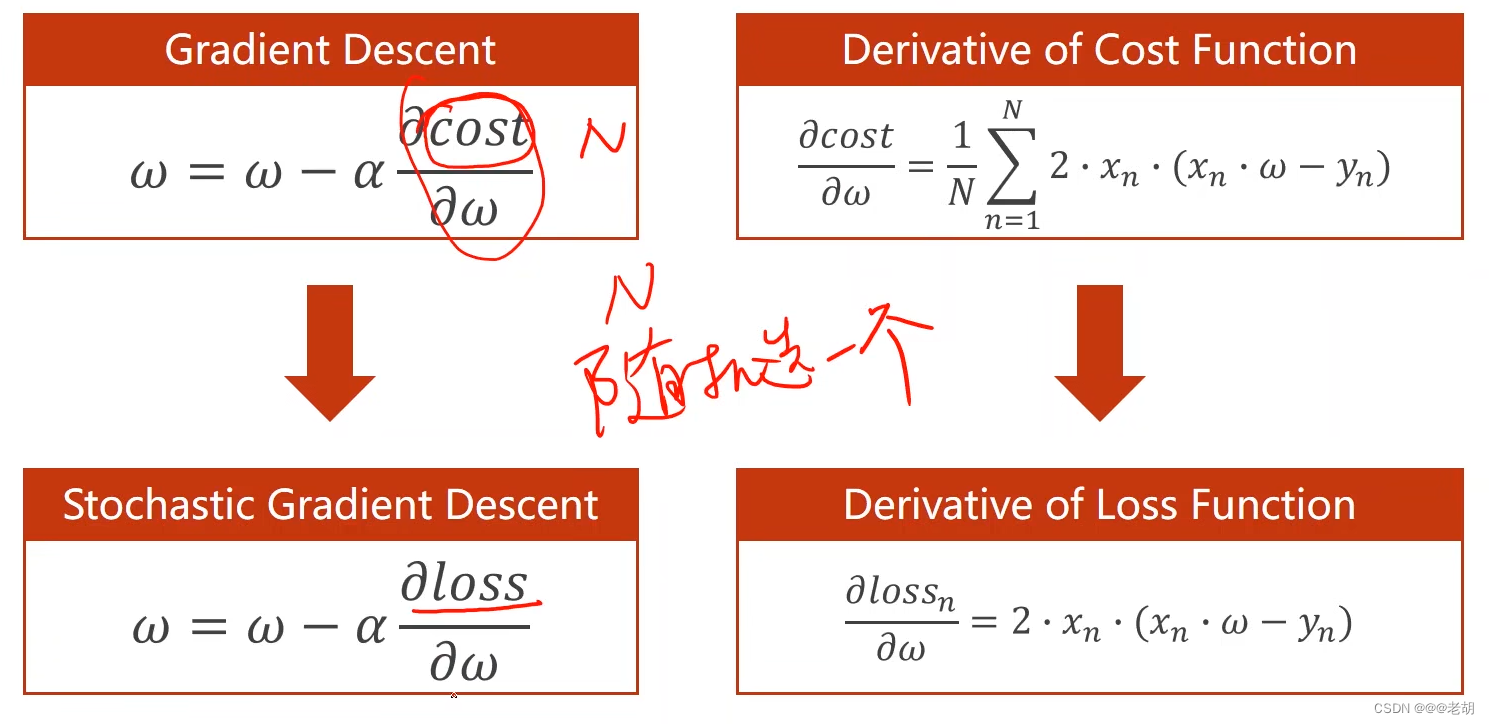
- 梯度下降
- 随机梯度下降
在线性模型训练的时候,一开始并不知道w的最优值是什么,可以使用一个随机值来作为w的初始值,使用一定的算法来对w进行更新
优化问题
寻找使得目标函数最优的权重组合的问题就是优化问题
梯度下降
通俗的讲,梯度下降就是使得梯度往下降的方向,也就是负方向走。一般来说,梯度往正方向走,表示梯度大于0,,表示函数是往递增方向走,而这里需要的是找最低点,最低点一定是在往下走,所以这里的梯度要取负号。梯度下降更新权重的公式如下(注意是减),α表示学习率:

梯度下降算法属于贪心算法的一种,它的权重的更新,每一次都是朝着梯度下降最快的方向进行更新,当梯度为0的时候,算法收敛,权重不再更新。梯度下降可能得到的是一个局部最优解(非凸函数)。
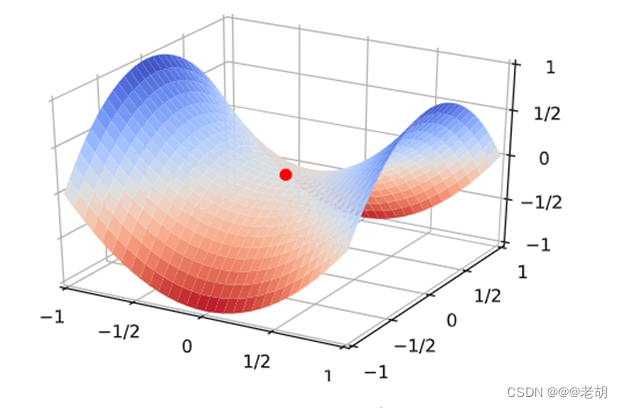
在深度学习中,尽管梯度下降算法会陷入局部最优,但是在深度学习中梯度下降算法依旧广泛应用:在之前大家认为,深度学习的目标函数会出现很多的局部最优解,但是实际上,其损失函数并没有很多的局部最优解。但是深度学习的损失函数会存在很多的鞍点(也就某一点上梯度为0,从一个切面上看是最小值,从另一个切面看是最大值的点,如下图 ),导致权重无法继续迭代,可以使用动量法来解决鞍点问题。


代码实现:
-
要求:模拟梯度下降算法,计算在x_data、y_data数据集下,y=w*x模型找到合适的w的值。
-
和第二课不同的是,第一课的w是我们认为设定的,通过一个for循环使得w迭代,这一次需要的是通过模型找到适合的w
import matplotlib.pyplot as pltx_data=[1.0,2.0,3.0]
y_data=[2.0,4.0,6.0]w=1.0
# 求预测值
def forward(x):return x*w# 损失函数
def cost(xs,ys):costs=0# 用zip打包成元祖,并返回元祖组成的列表for x,y in zip(xs,ys):y_pred=forward(x)costs+=(y_pred-y)**2 return costs/len(xs)# 计算梯度
def gradient(xs,ys):grad=0for x,y in zip(xs,ys):grad+=2*x*(x*w-y)return grad/len(xs)cost_list=[]
epoch_list=[]
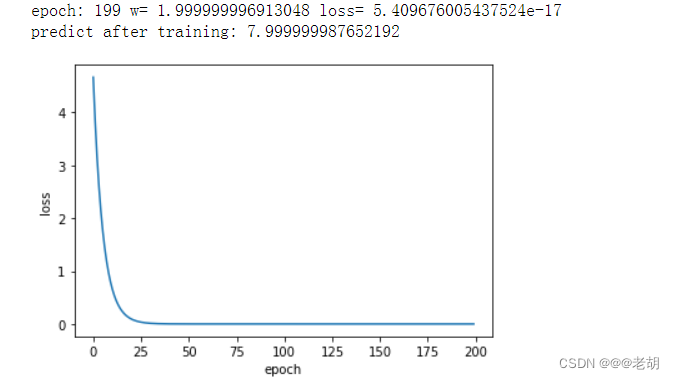
print('predict before training',forward(4))for epoch in range(200):cost_val=cost(x_data,y_data)grad_val=gradient(x_data,y_data)w-=0.01*grad_valepoch_list.append(epoch)cost_list.append(cost_val)print('epoch:',epoch,'w=',w,'loss=',cost_val)print('predict after training:',forward(4))# 画图
plt.plot(epoch_list,cost_list)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
部分结果截图
随机梯度下降
在上面的梯度下降中,求损失的时候用的是全部数据的平均损失作为更新的依据。而随机梯度下降是在全部的数据中随机选择一个作为更新的依据。使用随机梯度下降可以有效的避开鞍点
import matplotlib.pyplot as pltx_data=[1.0,2.0,3.0]
y_data=[2.0,4.0,6.0]w=1.0
# 求预测值
def forward(x):return x*w# 损失函数
def cost(x,y):y_pred=forward(x)return (y_pred-y)**2# 计算梯度
def gradient(x,y):return 2*x*(x*w-y)cost_list=[]
epoch_list=[]
print('predict before training',forward(4))for epoch in range(200):for x,y in zip(x_data,y_data):grad_val=gradient(x,y)print('\tgrad:',x,y,w)w-=0.01*grad_valprint('\tgrad:',x,y,w,'\n')cost_val=cost(x,y)epoch_list.append(epoch)cost_list.append(cost_val)print('epoch:',epoch,'w=',w,'loss=',cost_val)print('predict after training:',forward(4))# 画图
plt.plot(epoch_list,cost_list)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
结果截图:
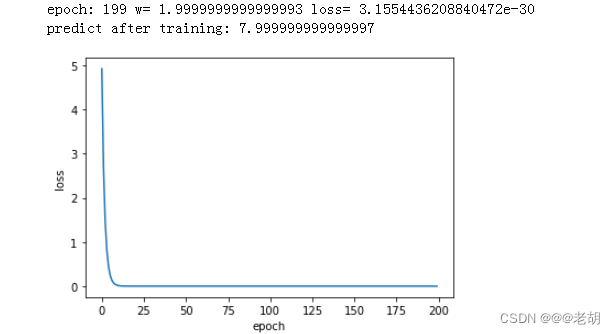
在第一个梯度下降中,样本x与样本x+1之间没有时序关系,我们计算的是他们的总的损失,这些运行时可以并行运行的。但是在第二个随机梯度下降中,我们是先计算了x再计算的x+1,数据之间存在先后的关系,有依赖关系,不能用并行计算。所以梯度下降可以有效提高运算的效率,而随机梯度下降可以获得一个优异的w。把以上两种方法折中,就产生了小批量随机梯度下降,取了一种性能与时间复杂度之间的折中。