适用情况
处理由试验、测量得到的大量数据或一些过于复杂而不便于计算的函数表达式时，构造一个简单函数作为要考察数据或复杂函数的近似
定义
给定一组数据，需要确定满足特定要求的曲线（或曲面）
插值：如果所求曲线通过所给定有限个数据点
拟合：要求所求曲线反映对象整体的变化态势，得到简单实用的近似函数

插值

在一系列数据点对中，一些数据点的函数值缺失，因而希望通过已有数据点得到函数的近似表达式从而近似出确实数据点的函数值

从性质优良、便于计算的函数类{P(x)}中选择一个使得$P(x_i)=y_i$成立的P(x)作为f(x)的近似
$x_0,x_1,...,x_n$成为插值节点
{ P ( x ) } \{P(x)\} {P(x)}称为插值函数类
$P(x_i)=y_i(i=0,1,...,n)$称为插值条件
得到的$P(x)$称为插值函数
$f(x)$称为被插值函数

一维插值方法：一维Lagrange插值、分段线性插值、分段二次插值、牛顿插值和样条插值
二维插值方法：二维样条插值

插值方法

Lagrange插值
$$P(x)=\sum _{i=0}^n{l}_i(x)y_i$$
其中$l_i(x)$称为以$x_0,x_1,...,x_n$为节点的Lagrange插值基函数
$$l_i(x)=\prod _{j=0,j\ne i}^n\frac{x-x_j}{x_i-x_j}$$

代码实现

def h(x,y,a):s = 0.0for i in range(len(y)):t = y[i]for j in range(len(y)):if i != j:t *= (a-x[j])(x[i]-x[j])s += treturn s

分段线性插值
用折线代替曲线$y=f(x)$，其中$P(x)$为
$$P(x)=\frac{x-x_i}{x_{i+1}-x_i}{y}_{i+1}+\frac{x-x_{i+1}}{x_i-x_{i+1}}{y}_i$$
其中 $x\in [x_i,x_{i+1}],i=0,1,...,n-1$

分段二次插值
$P(x)$为一二次多项式，即适用分段抛物线代替$y=f(x)$

牛顿插值
差分定义：函数$f(x)$，等距节点$x_i=x_0+ih(i=0,1,...,n)$，一阶前向差分$\Delta f_i=f_{i+1}-f_i$， 高阶差分为差分的差分

1. ${\Delta }^{0}f(x)=f(x)$
2. ${\Delta }^{m}f(x)={\Delta }^{m-1}f(x+h)-{\Delta }^{m-1}f(x)$

递归函数计算差分

def diff_forward(f, k, h, x):if k<=0: return f(x)else: return diff_forward(f, k-1, h, x+h) - diff_forward(f, k-1, h, x)

差商定义：函数$f(x)$，相异节点$x_0<x_1<...<x_n$
函数$f(x)$关于节点$x_i$，$x_j$的一阶差商 $f[x_i,x_j]$有
$$f[x_i,x_j]=\frac{f(x_i)-f(x_j)}{x_i-x_j}$$
$f(x)$关于点$x_i$，$x_j$，$x_k$的二阶差商有
$$f[x_i,x_j,x_k]=\frac{f[x_i,x_j]-f[x_j,x_k]}{x_i-x_k}$$
$f(x)$关于$x_0,x_1,...,x_k$的$k$阶差商为
$$f[x_0,x_1,...,x_k]=\frac{f[x_0,x_1,...,x_{k-1}]-f[x_1,x_2,...,x_k]}{x_0-x_k}$$

代码示例：计算$k+1$个点对数据的$k$阶差商

def diff_quo(xi=[], fi=[]):if len(xi)>2 and len(fi)>2:return (diff_quo(xi[:len(xi)-1],fi[:len(fi)-1])-diff_quo(xi[1:len(xi)],fi[1:len(fi)])) / float(xi[0]-xi[-1])  return (fi[0]- fi[1])/float(xi[0]-xi[1])

Newton插值公式
一次Newton插值多项式：$N_1(x)=f(x_0)+(x-x_0)f[x_0,x_1]$
再根据各阶差商的定义，可以得到$N_n(x)$即$f(x)$的$n$次插值多项式

样条插值
适用于对插值函数的光滑性有较高要求的问题
样条函数：具有一定光滑性的分段多项式
给定$[a,b]$的一个分划，$\Delta :a=x_0<x_1<...<x_n=b$
若$S(x)$在各个小区间$[x_i,x_{i+1}](i=0,1,...,n-1)$上为$m$次多项式，且有$m-1$阶连续导数，称$S(x)$为关于分划$\Delta$的$m$次样条函数，折线属于一次样条曲线

二维数据的双三次样条插值
考虑二维数据的插值时，需要考虑到插值区域是否规则，给定数据是有规律分布的还是散乱、随机分布的
当二维数据在规则区域上有规律分布时，可以考虑用双三次样条插值，即求解一个$S(x)$满足对$x$和$y$都是三次的多项式

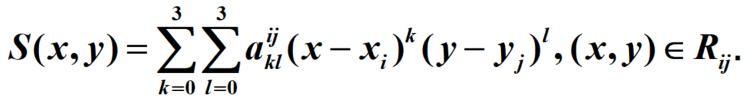
用Python解决插值问题

scipy.interpolatemodule有一维插值函数interp1d、二维插值函数interp2d和多维插值函数interpn

一维插值
interp1d(x, y, kind='linear')
说明：kind参数取值为字符串，指明插值方法，取值包括linear线性插值、zero0阶样条插值、slinear1阶样条插值、quadratic2阶样条插值、cubic3阶样条插值

代码

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d 
x=np.arange(0,25,2)
y=np.array([12, 9, 9, 10, 18, 24, 28, 27, 25, 20, 18, 15, 13])
xnew=np.linspace(0, 24, 500)  #插值点
f1=interp1d(x, y); 
y1=f1(xnew);
f2=interp1d(x, y,'cubic'); 
y2=f2(xnew)
plt.rc('font',size=16); 
plt.rc('font',family='SimHei')
plt.subplot(121)
plt.plot(xnew, y1)
plt.xlabel("（A）分段线性插值")
plt.subplot(122)
plt.plot(xnew, y2)
plt.xlabel("（B）三次样条插值")
plt.savefig("figure7_4.png", dpi=500)
plt.show()

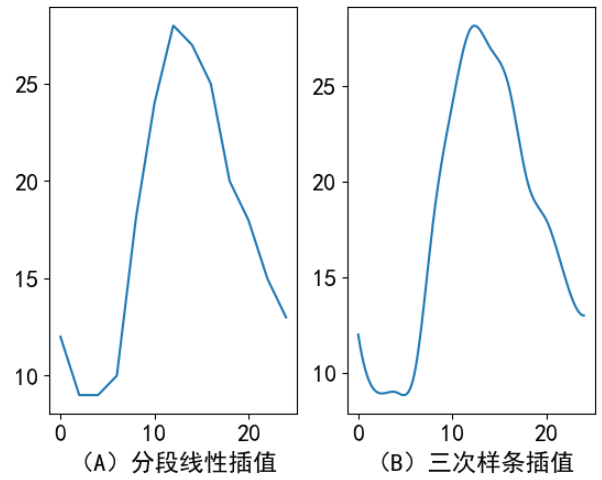
二维网格节点插值

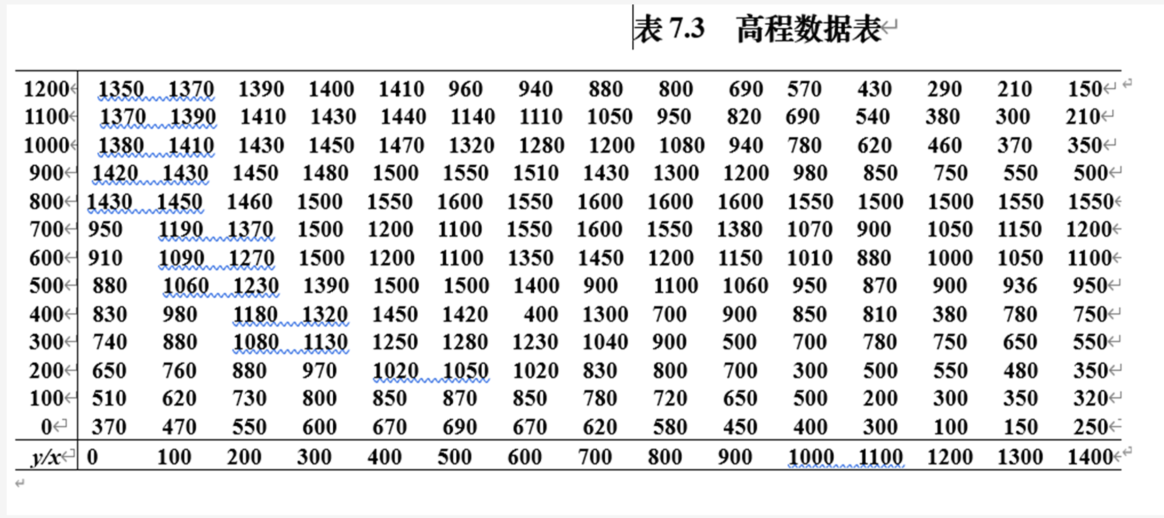
思路：原始数据为100x100网格节点的数据，为提高精度，适用双三次样条插值，得到该区域上10x10网格节点的数据。把$0\le x\le 1400\wedge 0\le y\le 1200$ 数据分为140x120个小矩形计算对应曲面面积，每个矩形分为两个三角形，再利用海伦公式求解
代码：

from mpl_toolkits import mplot3d
import matplotlib.pyplot as plt
import numpy as np
from numpy.linalg import norm
from scipy.interpolate import interp2d
z=np.loadtxt("Pdata7_5.txt")  #加载高程数据
x=np.arange(0,1500,100)
y=np.arange(1200,-100,-100)
f=interp2d(x, y, z, 'cubic')
xn=np.linspace(0,1400,141)
yn=np.linspace(0,1200,121)
zn=f(xn, yn)
m=len(xn); n=len(yn); s=0; 
for i in np.arange(m-1):for j in np.arange(n-1):p1=np.array([xn[i],yn[j],zn[j,i]])p2=np.array([xn[i+1],yn[j],zn[j,i+1]])p3=np.array([xn[i+1],yn[j+1],zn[j+1,i+1]])p4=np.array([xn[i],yn[j+1],zn[j+1,i]])p12=norm(p1-p2); p23=norm(p3-p2); p13=norm(p3-p1);p14=norm(p4-p1); p34=norm(p4-p3);L1=(p12+p23+p13)/2;s1=np.sqrt(L1*(L1-p12)*(L1-p23)*(L1-p13));L2=(p13+p14+p34)/2; s2=np.sqrt(L2*(L2-p13)*(L2-p14)*(L2-p34));s=s+s1+s2;  
print("区域的面积为：", s)
plt.rc('font',size=16); plt.rc('text',usetex=True)
plt.subplot(121); contr=plt.contour(xn,yn,zn); plt.clabel(contr)
plt.xlabel('$x$'); plt.ylabel('$y$',rotation=90)
ax=plt.subplot(122,projection='3d'); 
X,Y=np.meshgrid(xn,yn)
ax.plot_surface(X, Y, zn,cmap='viridis')
ax.set_xlabel('$x$'); ax.set_ylabel('$y$'); ax.set_zlabel('$z$')
plt.savefig('figure7_5.png',dpi=500); plt.show()

二维乱点插值

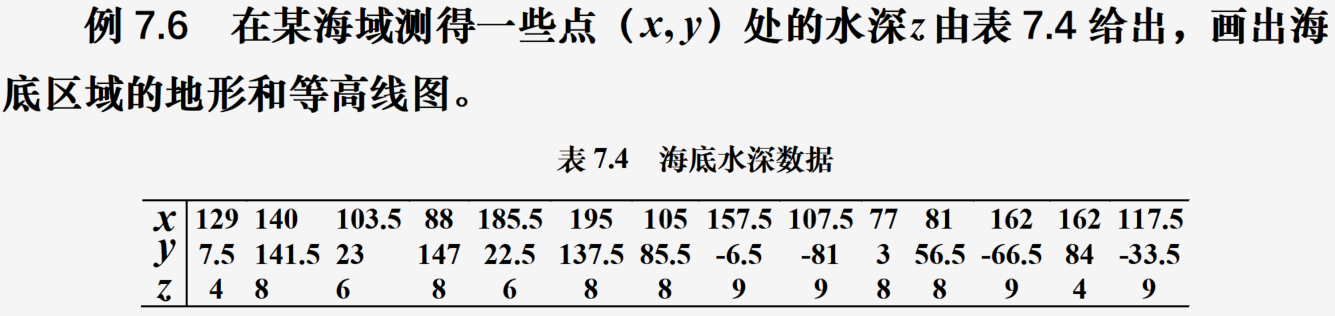
代码：

from mpl_toolkits import mplot3d
import matplotlib.pyplot as plt
import numpy as np
from scipy.interpolate import griddata
x=np.array([129,140,103.5,88,185.5,195,105,157.5,107.5,77,81,162,162,117.5])
y=np.array([7.5,141.5,23,147,22.5,137.5,85.5,-6.5,-81,3,56.5,-66.5,84,-33.5])
z=-np.array([4,8,6,8,6,8,8,9,9,8,8,9,4,9])
xy=np.vstack([x,y]).T
xn=np.linspace(x.min(), x.max(), 100)
yn=np.linspace(y.min(), y.max(), 100)
xng, yng = np.meshgrid(xn,yn)  #构造网格节点
zn=griddata(xy, z, (xng, yng), method='nearest')  #最近邻点插值
plt.rc('font',size=16); plt.rc('text',usetex=True)
ax=plt.subplot(121,projection='3d'); 
ax.plot_surface(xng, yng, zn,cmap='viridis')
ax.set_xlabel('$x$'); ax.set_ylabel('$y$'); ax.set_zlabel('$z$')
plt.subplot(122); c=plt.contour(xn,yn,zn,8); plt.clabel(c)
plt.savefig('figure7_6.png',dpi=500); plt.show()

拟合

最小二乘拟合

解决什么问题？
已知一组二维数据，即平面上$n$个点$(x_i,y_i)(i=1,2,...,n)$，$x_i$互不相同，求函数$f(x)$使得$f(x)$在某种准则下与所有数据点最为接近，即曲线拟合得最好
残差：${\delta }_i=f(x_i)-y_i,i=1,2,...,n$
最小二乘法使用的判定准则为残差的平和和最小，即
$$argminJ=\sum _{i=1}^n(f(x_i)-y_i{)}^2$$
最终得到拟合函数$f(x)=f(x,a_1,a_2,...,a_n)$
根据参数$a_1,a_2,...,a_n$线性与否，最小二乘法分为线性最小二乘和非线性最小二乘

线性最小二乘法
给定线性无关的函数系 { ϕ k ( x ) ∣ k = 1 , 2 , . . . , m } \{\phi_k(x)|k=1,2,...,m\} {ϕk​(x)∣k=1,2,...,m}
若有拟合函数$f(x)={\sum }_{k=1}^m{a}_k{\varphi }_k(x)$，例如$f(x)=a_m{x}^{m-1}+a_{m-1}{x}^{m-2}+...+a_{2}x+a_1$ 或$f(x)={\sum }_{k=1}^m{a}_{k}cos(kx)$
称 $f(x)=f(x,a_1,a_2,...,a_m)$为关于参数$a_1,a_2,...,a_m$的线性函数
将$f(x)$带入$J$的计算，根据
$$\frac{\partial J}{\partial a_k}=0,k=1,2,\cdots ,m$$
即：
$$\sum _{i=1}^n\left[\left(f\left(x_i\right)-y_i\right){\phi }_k\left(x_i\right)\right]=0,k=1,2,\cdots ,m$$
得到：

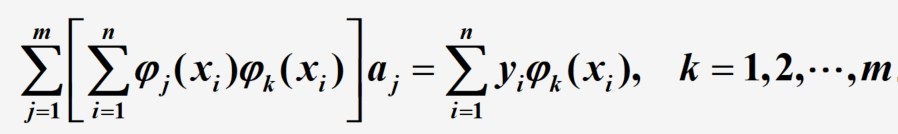
形成一个关于$a_1,a_2,...,a_m$的线性方程组，记号说明如下：

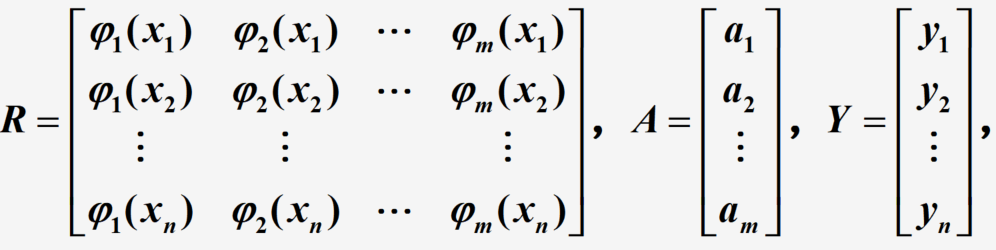
则正规方程组改写为
$$R^{T}RA=R^{T}Y$$
当矩阵$R$列满秩时，$R^{T}R$可逆，此时正规方程组有唯一解，即
$$A=(R^{T}R{)}^{-1}{R}^{T}Y$$
非线性最小二乘拟合
当拟合函数不能以${\varphi }_k(x)$线性组合的形式构成时，例如下列形式：

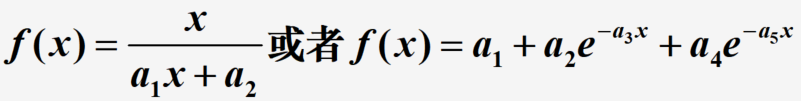
使用同样的“最小化偏差”方法求解参数

拟合函数的选择
先做出数据的散点图，从直观上判断应选用什么样的拟合函数
举个例子
若数据分布接近直线，使用线性函数$f(x)=a_{1}x+a_2$
若数据分布接近抛物线，使用二次多项式$f(x)=a_1{x}^2+a_{2}x+a_3$
若数据分布是开始上升块随后逐渐变缓，使用双曲线型函数或指数型函数，即

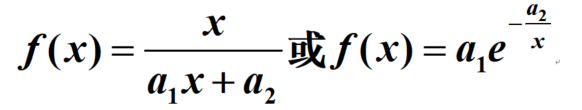
若数据分布是开始下降较快随后逐渐变缓，使用

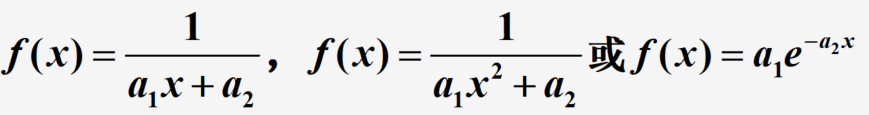
数据拟合的Python实现

利用NumPy库中的多项式拟合函数polyfit或scipy.optimize模块中的curve_fit函数

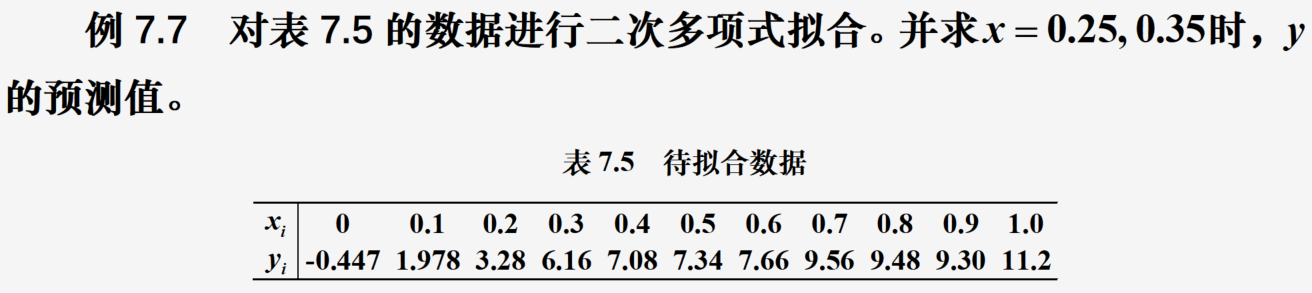
polyfit的用法
代码展示：

from numpy import polyfit, polyval, array, arange
from matplotlib.pyplot import plot,show,rc
x0=arange(0, 1.1, 0.1)
y0=array([-0.447, 1.978, 3.28, 6.16, 7.08, 7.34, 7.66, 9.56, 9.48, 9.30, 11.2])
p=polyfit(x0, y0, 2) #拟合二次多项式
print("拟合二次多项式的从高次幂到低次幂系数分别为:",p)
yhat=polyval(p,[0.25, 0.35]); print("预测值分别为：", yhat)
rc('font',size=16)
plot(x0, y0, '*', x0, polyval(p, x0), '-'); show()

curve_fit的用法
调用格式
popt, pcov = curve_fit(func, xdata, ydata)
参数说明：func为拟合的函数，xdata是自变量的观测值，ydata是函数的观测值，返回值popt是拟合的参数，pcov是参数的协方差矩阵
代码展示：

import numpy as np
from scipy.optimize import curve_fit
y=lambda x, a, b, c: a*x**2+b*x+c
x0=np.arange(0, 1.1, 0.1)
y0=np.array([-0.447, 1.978, 3.28, 6.16, 7.08, 7.34, 7.66, 9.56, 9.48, 9.30, 11.2])
popt, pcov=curve_fit(y, x0, y0)
print("拟合的参数值为：", popt)
print("预测值分别为：", y(np.array([0.25, 0.35]), *popt))

实例练习

代码：

import numpy as np
from scipy.optimize import curve_fit
x0=np.array([6, 2, 6, 7, 4, 2, 5, 9])
y0=np.array([4, 9, 5, 3, 8, 5, 8, 2])
z0=np.array([5, 2, 1, 9, 7, 4, 3, 3])
xy0=np.vstack((x0, y0))
def Pfun(t, a, b, c):return a*np.exp(b*t[0])+c*t[1]**2
popt, pcov=curve_fit(Pfun, xy0, z0)
print("a，b，c的拟合值为：", popt)

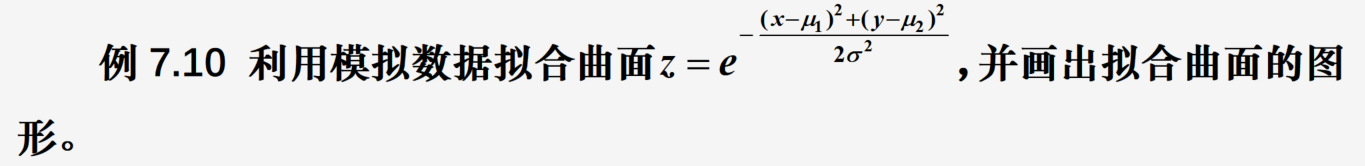
代码：

from mpl_toolkits import mplot3d
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
m=200; n=300
x=np.linspace(-6, 6, m); y=np.linspace(-8, 8, n);
x2, y2 = np.meshgrid(x, y)
x3=np.reshape(x2,(1,-1)); y3=np.reshape(y2, (1,-1))
xy=np.vstack((x3,y3))
def Pfun(t, m1, m2, s):return np.exp(-((t[0]-m1)**2+(t[1]-m2)**2)/(2*s**2))
z=Pfun(xy, 1, 2, 3); zr=z+0.2*np.random.normal(size=z.shape) #噪声数据
popt, pcov=curve_fit(Pfun, xy, zr)   #拟合参数
print("三个参数的拟合值分别为：",popt)
zn=Pfun(xy, *popt)  #计算拟合函数的值
zn2=np.reshape(zn, x2.shape)
plt.rc('font',size=16)
ax=plt.axes(projection='3d') #创建一个三维坐标轴对象
ax.plot_surface(x2, y2, zn2,cmap='gist_rainbow')
plt.savefig("figure7_10.png", dpi=500); plt.show()