马尔可夫预测（Python）

马尔科夫链（Markov Chains）

从一个例子入手：假设某餐厅有A，B，C三种套餐供应，每天只会是这三种中的一种，而具体是哪一种，仅取决于昨天供应的哪一种，换言之，如果知道今天供应了什么，就可以用某种方式预测明天将会供应什么。

例如，今天供应的是A，那么明天有60%概率供应B，我们可以用一条由A向B的有向边来表示，边权是概率。于是我们可以用图来表示这种关系：

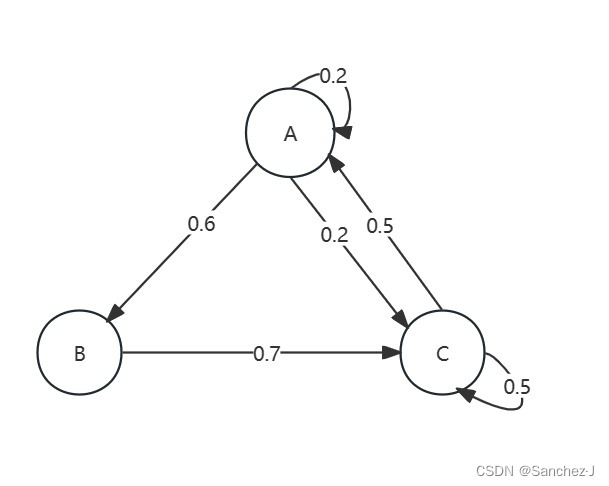
这就是一个马尔科夫链。

马尔科夫链的一个重要状态就是未来状态只取决于现在状态而与过去无关。

也就是有

$P(X_{n+1}=x | X_1=x_1,...,X_n=x_n)=P(X_{n+1}=x | X_n=x_n)$

例如考虑已知一个供应序列[B,A,B]，那么第4天供应C的概率是多少？由马尔可夫性质，我们只需要考虑第3天，因此概率就是70%。

下面我们在链上做随机漫步（Random Walk），比如得到结果[A, B, A, C, A, C, C, C, A, B]，现在我们想要求出每种套餐的概率，直接用频率分布近似，而长期下来，这些概率（可能）会收敛到某些特定值，这种概率分布叫做稳态分布。

我们亦可用线性代数来求出稳态的概率分布，对于有向图，我们可以转化为邻接矩阵:

$M = \begin{bmatrix} 0.2 & 0.6 &0.2 \\ 0.3& 0 &0.7 \\ 0.5 & 0 &0.5 \end{bmatrix}$

我们用一个行向量 $\pi$ 来代表状态的概率，假设我们从B状态开始，则有

$\pi_0=\begin{bmatrix} 0 & 1 & 0 \end{bmatrix}$

当我们将这个行向量和矩阵相乘，我们得到了矩阵的第二行，更广义地，我们得到了未来的状态。

$\pi_1 = \pi_0M$

依次类推，那么我们可以说，如果在某一次达到了稳态，那么输出的行向量应当等于输入的行向量，于是我们得到了这个在线性代数中熟悉的表达式

$\pi M=\pi$

因此 $\pi$ 其实是矩阵的特征向量，特征值等于1，此外 $\pi$ 的元素还需要满足归一性，也即全部元素之和等于1。

由此我们可以解出这个稳态： $\pi=[\frac{25}{71},\frac{15}{71},\frac{31}{71}]$ ，这个结果和直接模拟得到的相符合。

这个结果告诉我们，餐厅整体上会在大概35%的时间供应A，21%的时间供应B，剩下时间供应C。

由此我们也可以看出可能存在多个稳态，取决于有多少个满足条件的特征向量。

现在考虑下面这个马尔科夫链：

我们会发现对于状态0只要离开就不可能再回去了，这种不可被其他状态达到的情况我们称为暂态（transient）。

而对于状态1、2离开后是可以回来的，称为常返状态（Recurrent）

而当存在暂态时，我们称这个马尔科夫链是可约的；反之称不可约链。

这里我们如果把0->1这条边删去，可以得到两个更小的不可约链。

现在考虑下面这个马尔科夫链

$A=\begin{bmatrix} 0.5 &0.2 &0.3 \\ 0.6&0.2 &0.2 \\ 0.1& 0.8 &0.1 \end{bmatrix}$

考虑这个问题：

从状态i到状态j共n步的概率（ $P_{ij}(n)$ ）是多大？

可以先考虑简单的， $P_{02}(1)$ 显然等于 $A_{02}$

而对于 $P_{02}(2)$ ，我们需要考虑所有可能的路径，并将概率相加: $A_{01}\times A_{12} + A_{00}\times A_{02}+A_{02}\times A_{22}$

这个表达式其实是两个向量乘积 $\begin{bmatrix} A_{00} & A_{01} &A_{02} \end{bmatrix}\times\begin{bmatrix} A_{02}\\ A_{12}\\ A_{22} \end{bmatrix}$

由此我们可以总结 $P_{ij}(2)=A^2_{ij}$

进一步 $P_{ij}(n)=A^n_{ij}$

这样的总结是根据经验的归纳，不能保证正确。

但确实是正确的，根据是Chapman-Kolmogorov定理，之所以能使用，是因为马尔可夫性质。

该定理表述如下：

$P_{ij}(n)=\sum_{k}P_{ik}(r)\times P_{kj}(n-r)$

现在我们从另一个视角来看稳态分布，我们让n趋于无穷大

$\lim_{n \to \infty}A^n=\begin{bmatrix} 0.4444 &0.3333 &0.2222 \\ 0.4444 &0.3333 &0.2222 \\ 0.4444&0.3333 & 0.2222 \end{bmatrix}$

每一行都收敛到同一个行向量，这就是这个马尔科夫链的静态分布。

比如对于 $A_{ij}^\infty=P_{ij}(\infty)$ ，对于不同的i其值是不变的，换言之，不依赖于开始的状态，这恰恰符合马尔可夫性质。

隐马尔科夫链（Hidden Markov Model）

仍然从例子入手：

Jack 所住的地方只有三种天气A，B，C，任何一天只会出现一种天气，明天天气只和今天天气相关。假设Jack每天有两种可能的心情a、b，心情取决于天气。如下图

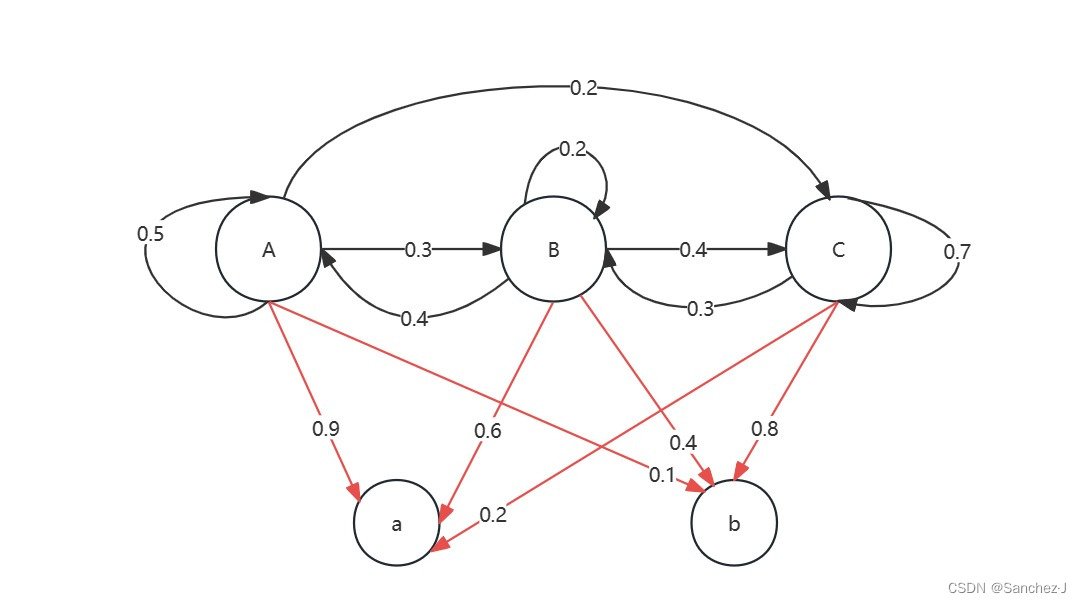
现在我们不知道某一天的天气情况，但是我们可以了解Jack的情绪，因此说马尔科夫链的状态是隐藏的，我们可以观察到一些依赖于这些状态的变量。可以说，隐马尔可夫模型就是一个普通的马尔科夫链和一组观测变量构成，即

HMM = HiddenMC + Observed Variables

注意：Jack的情绪只和当天的天气有关而和昨天的情绪无关

同样我们可以用矩阵表示

转移矩阵： $\begin{bmatrix} 0.5 &0.3 &0.2 \\ 0.4 &0.2 &0.4 \\ 0.0& 0.3 &0.7 \end{bmatrix}$

发射矩阵（记录观测变量相应概率的矩阵）： $\begin{bmatrix} 0.9 &0.1 \\ 0.6 & 0.4\\ 0.2 &0.8 \end{bmatrix}$

现在考虑连续三天的情况

这里先假设我们知道天气情况，那么这种情况的概率我们可以算出来：

其中第一项 $P(X_1=C)$ 需要用求平稳分布得到，其余项可以直接从矩阵读出。

现在我们隐藏状态，只看观察变量的序列，最有可能的状态序列是什么？

要解决这个问题，我们需要计算每个序列的概率，找出概率最大的序列，而最终找出来确实是CBC这个序列。

Python模板代码

详见注释

from hmmlearn.hmm import GaussianHMM
# 导入 GaussianHMM 类，这是 hmmlearn 库中用于高斯混合模型（Gaussian Hidden Markov Model）的类。
import numpy as np
startprob = np.array([0.6, 0.3, 0.1, 0.0])
# 建一个 NumPy 数组 startprob，表示 HMM 模型的初始状态概率。
transmat = np.array([[0.7, 0.2, 0.0, 0.1],[0.3, 0.5, 0.2, 0.0],[0.0, 0.3, 0.5, 0.2],[0.2, 0.0, 0.2, 0.6]])
# 创建一个 NumPy 数组 transmat，表示 HMM 模型的状态转移矩阵。
means = np.array([[0.0,  0.0],[0.0, 11.0],[9.0, 10.0],[11.0, -1.0]])
# 表示每个隐藏状态的均值。
covars = .5 * np.tile(np.identity(2), (4, 1, 1))
# 表示每个隐藏状态的协方差矩阵。这里使用了 np.tile 来生成相同的协方差矩阵。
hmm = GaussianHMM(n_components=4, covariance_type='full')
# 创建一个 GaussianHMM 对象，指定模型有 4 个隐藏状态，并使用完整的协方差矩阵
hmm.startprob_ = startprob
# 设置 HMM 模型对象的初始状态概率。
hmm.transmat_ = transmat
# 设置 HMM 模型对象的状态转移矩阵。
hmm.means_ = means
# 设置 HMM 模型对象的均值。
hmm.covars_ = covars
# 设置 HMM 模型对象的协方差矩阵。
seen = np.array([[1.1, 2.0], [-1, 2.0], [3, 7]])
# seen表示观察到的数据序列。
logprob, state = hmm.decode(seen, algorithm="viterbi")
# 使用 Viterbi 算法对给定的观察数据序列进行解码，返回对数概率和对应的状态序列。
print(state)
print(hmm.score(seen))

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/245586.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！