1.分类算法
分类算法是有监督学习的一个核心问题,他从数据中学习一个分类决策函数或分类模型,对新的输入进行预测,输出变量取有限个离散值。
🌍分类算法的内容是要求给定特征,让我们得出类别。
那么如何由指定特征,得到我们最终的类别呢,每一个不同的分类算法,对应着不同的核心思想。
以下是一些常见的分类算法:
-
逻辑回归 (Logistic Regression):
用于二分类问题,通过逻辑函数将输入映射到0和1之间的概率。 -
K近邻算法 (K-Nearest Neighbors, KNN):
基于输入数据点在特征空间中的邻近程度,将其分为最接近的K个邻居的多数类别。 -
决策树 (Decision Trees):
基于对输入数据进行递归分割,以最小化混淆或不确定性,从而创建树状结构来进行分类。 -
随机森林 (Random Forest):
通过集成多个决策树,每个树的投票决定最终的分类结果,提高模型的鲁棒性和泛化能力。 -
支持向量机 (Support Vector Machines, SVM):
构建一个超平面,最大化两个类别之间的间隔,用于二分类和多分类问题。 -
朴素贝叶斯 (Naive Bayes):
基于贝叶斯定理,假设输入特征之间是相互独立的,通过计算后验概率进行分类。 -
神经网络 (Neural Networks):
通过多个神经元和层的组合,学习非线性关系,适用于复杂的问题和大规模数据。 -
梯度提升机 (Gradient Boosting Machines):
通过逐步构建多个弱分类器(通常是决策树),每个都纠正前一个的错误,从而提高整体模型性能。 -
Adaboost (Adaptive Boosting):
类似于梯度提升,但是每个弱分类器的权重是根据前一个分类器的性能来调整的。 -
XGBoost (Extreme Gradient Boosting):
是一种梯度提升算法的变种,通过更加高效的实现和正则化技术,提高了性能。
选择合适的分类算法通常取决于数据的性质、问题的复杂程度以及模型的性能要求。在实际应用中,往往需要尝试多种算法,并通过交叉验证等技术来评估它们的性能。
朴素贝叶斯
1.数学基础
先验概率(Prior Probability):
-
先验概率是在考虑任何新观测数据之前,基于先前的知识或信仰,对事件发生的概率的初始估计。这是对事件的主观先验信仰或经验的量化体现。
-
记作 P(A),表示事件 A 在考虑新的观测数据之前的概率。先验概率可以基于领域专家的经验、历史数据或任何相关信息。
🌍先验概率,就是由以往的数据分析所得。
后验概率(Posterior Probability):
-
在观测到新数据之后,通过贝叶斯定理计算得到的更新概率,即在考虑了先验概率的基础上,考虑新的观测数据后事件发生的概率。
-
记作 P(A|B),表示在给定观测数据 B 的情况下,事件 A 发生的概率。这是基于新的数据调整过的概率。
🌍后验概率,在得到信息之后重新加以修正得到的概率。
2.叶斯决策论
2.1 贝叶斯定理
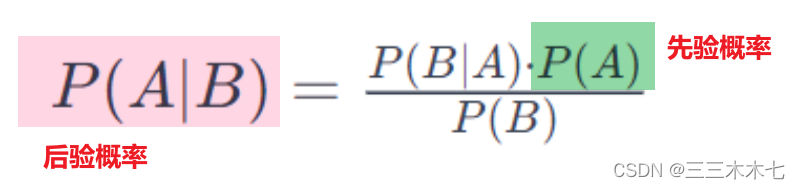
其中:
- P(A∣B) 是后验概率,表示在给定观测到 B 的情况下,事件 A 发生的概率。
- P(B∣A) 是似然度,表示在事件 A 发生的情况下观测到 B 的概率。
- P(A) 是先验概率,表示在考虑观测数据 B 之前事件 A 发生的概率。
- P(B) 是边缘似然度,表示观测到数据 B 的概率。
-
先验概率 P(A): 在考虑观测到任何新数据 B 之前,我们对事件 A 的初始信仰,即在没有新证据的情况下,事件 A 发生的概率。
-
似然度 P(B∣A): 在事件 A 发生的条件下,观测到数据 B 的概率。这描述了事件 A 对观测数据 B 的影响。
-
边缘似然度 P(B): 观测到数据 B 的概率,考虑所有可能的事件。它是一个归一化因子,确保后验概率 P(A∣B) 在所有可能的事件 A 下加和为1。
-
后验概率 P(A∣B): 在观测到数据 B 之后,事件 A 发生的概率。这是通过将先验概率与新的证据(似然度)结合起来得到的。
2.2 贝叶斯决策论
【贝叶斯决策论】:是一种基于贝叶斯统计学的决策方法,它通过考虑先验概率、似然度以及决策损失来做出最优决策。这种方法可以应用于各种决策问题,包括分类、回归和其他决策场景。
通俗理解:
【贝叶斯决策】: 在贝叶斯决策理论中,我们希望选择那个最小化总体期望损失的决策。决策损失的期望值通过对所有可能状态的加权平均来计算,其中权重是先验概率。

🌍我们的任务是寻找一个判定标准,以最小化总体期望损失。
决策过程:
-
计算后验概率: 使用贝叶斯定理计算在给定观测数据的情况下,每个可能状态的后验概率。
-
计算期望损失: 对于每种可能的决策,计算总体期望损失。
-
选择最小化期望损失的决策: 选择那个使期望损失最小的决策,即选择总体期望损失最小的决策。
专业解释:
贝叶斯决策论(Bayesian decision theory)是在概率框架下实施决策的基本方法。
在分类问题情况下,在所有相关概率都已知的理想情形下,贝叶斯决策考虑如何基于这些概率和误判损失来选择最优的类别标记。

【解读】:
N种可能的类别标记,分别为
,
是将一个样本分错类后产生的损失。
一个事件为将真实标记为
的样本误分类为
,它的总体期望损失是
=【如上那堆式子】
(其实也就是这个事件发生的概率 x 这个事件的损失值)
🌍我们的任务是寻找一个判定准则
来使总体期望损失最小。

【解读】:
对每个样本而言,如果判定准则
能够使这个样本的条件风险最小化,则总体风险也将被最小化。
然后就有了贝叶斯判定准则,也就是 在每个样本上选择使条件风险最小的类别样本 标记。

【解读】:
首先是损失
的计算:如果i=j,则损失记为0,否则损失记为1。
然是条件风险的计算,
2.3 应用
贝叶斯公式:

扩展如下:

用下面这个例子来解释:
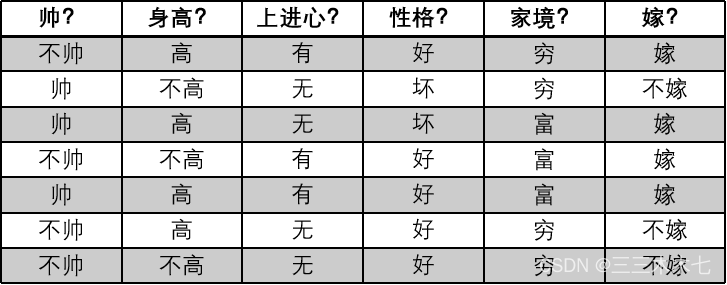
一对男女朋友,男生向女生求婚,男生的五个特点分别是不帅,不高,没有上进心,性格不好,家境贫寒,请你判断一下女生是嫁还是不嫁?
这是一个典型的分类问题,转为数学问题就是比较p(嫁|(不帅,不高,没有上进心,性格不好,家境贫寒))与p(不嫁|(不帅,不高,没有上进心,性格不好,家境贫寒))的概率,谁的概率大,我们就能给出嫁或者不嫁的答案!
这里我们联系朴素贝叶斯公式: