---

前言

本篇介绍的是有关方差知识的题目介绍。

---

例题

例题一

（数据：exercise7_3.RData）为研究上市公司对其股价波动的关注程度，一家研究机构对在主板、中小板和创业板上市的190家公司进行了调查，得到如下数据：检验上市公司的类型对股价波动的关注程度是否独立。（α=0.05）

解：提出假设：
H0: 上市公司的类型对股价波动的关注程度是独立的
H1：上市公司的类型对股价波动的关注程度是不独立的
计算期望频数与检验统计量

x<-c(50,70,30,15,20,5)
M<-matrix(x,nr=3,nc=2,byrow=TRUE,dimnames=list(c("主板企业","中小板企业","创业板企业"),c("关注","不关注")))
chisq.test(M)

在该项检验中，X2=16.854，P=0.0002189。由于P<0.05，拒绝H0，认为上市公司的类型对股价波动的关注程度不独立，是有关的。

例题二

数据：exercise7_3.RData）为研究上市公司对其股价波动的关注程度，一家研究机构对在主板、中小板和创业板上市的190家公司进行了调查，得到如下数据：计算上市公司的类型与对股价波动的关注程度两个变量之间的 系数、Cramer’sV系数和列联系数，并分析其相关程度。

library(vcd)
x<-c(50,70,30,15,20,5)
M<-matrix(x,nr=3,nc=2,byrow=TRUE,dimnames=list(c("主板企业","中小板企业","创业板企业"),c("关注","不关注")))
assocstats(M)

由于系数只用于2*2列联表的相关性度量，所以R输出结果为NA。Cramer’sV系数和列联系数均显示上市公司的类型与对股价波动的关注程度之间存在一定的相关性。

例题三

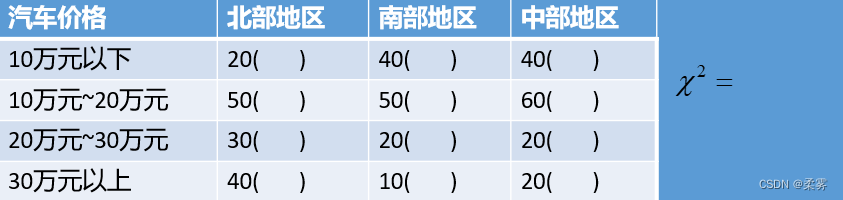
数据：exercise7_4.RData）一家汽车企业的销售部门对北部地区、中部地区和南部地区的400个消费者做了抽样调查，得到如下数据：

(1)利用公式求出期望频数以及 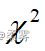统计量(写明步骤)，将结果填入上表括号内。
(2)检验地区与汽车价格是否独立( 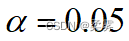)（利用R代码进行列联表独立性检验）。

解：提出假设：
H0: 地区与汽车价格是独立的
H1：地区与汽车价格是不独立的
计算期望频数与检验统计量

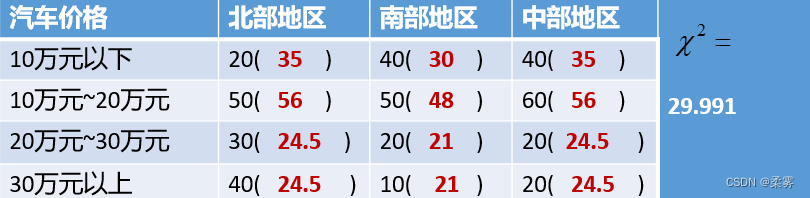
解：

x<-c(20,40,40,50,50,60,30,20,20,40,10,20)
M<-matrix(x,nr=4,nc=3,byrow=TRUE,dimnames=list(c("10万元以下","10万元~20万元","20万元~30万元","30万元以上"),c("北部地区","南部地区","中部地区")))
chisq.test(M)

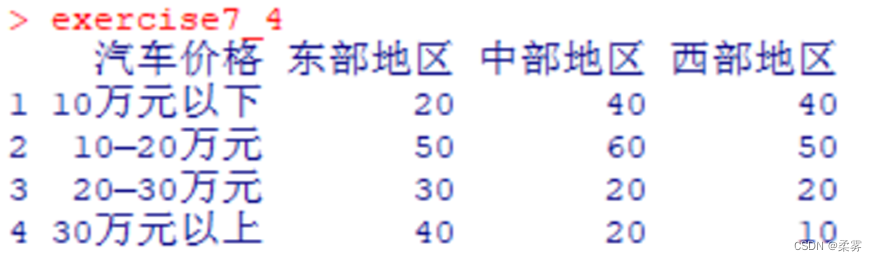
在该项检验中，X2=29.991，P= 3.946e-05。由于P<0.05，拒绝H0，认为地区和汽车价格不独立，是有关的。

例题四

（数据：exercise7_4.RData）一家汽车企业的销售部门对北部地区、中部地区和南部地区的400个消费者做了抽样调查，得到如下数据：

计算地区与汽车价格两个变量之间的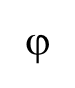系数、Cramer’sV系数和列联系数，并分析其相关程度。
解：

library(vcd)
assocstats(M)

由于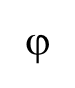系数只用于22列联表的相关性度量，所以R输出结果为NA。Cramer’sV系数和列联系数均显示地区与汽车价格之间存在一定的相关性。

例题五

215名病人中的39名被观测到患有哮喘，青原博士希望对“ 随机病人” 患有哮喘的概率是 0.15这个假设做检验。使用两种方法
解：提出假设：设“ 随机病人” 患有哮喘的概率为p
H0: p=0.15
H1： p 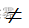0.15
在R里能用函数prop.test()来做检验：

>prop.test(39,215,.15) #三个参数分别是成功观测数，总数以及相对其检验的概率参数

1-sample proportions test with continuity correction
data: 39 out of 215, null probability 0.15
X-squared = 1.425, df = 1, p-value = 0.2326
alternative hypothesis: true p is not equal to 0.15
95 percent confidence interval:
0.1335937 0.2408799
sample estimates:
p
0.1813953
输出结果给出了单个总体比例的检验结果，即p-value = 0.2326>0.05，不能拒绝零假设
输出结果还给出了比例的点估计（0.1813953）和区间估计（[0.1335937,0.2408799]）
这里的0.15是人为构造出来的，如果没有设定的话，那么默认是0.5。但是如果我们有一组这样的数据，往往更希望得到这个概率参数的置信区间，这里输出结果的结尾已经给我们算好了。

例题六

青原博士在两个班级对同一教学方法的教学 效果进行了调查，第一个班级45个人，有23个人认为有效果，第二个班级40个人，有22个人认为有效果。检验第一个班级认为有教学效果的人的比例是否显著高于第二个班级？
H0：p1 =p2 H1：p1 >p2

success=c(23,22)
total=c(45,40)
prop.test(success,total,alt="greater")

2-sample test for equality of proportions with continuity
correction
data: success out of total
X-squared = 0.0198, df = 1, p-value = 0.556
alternative hypothesis: greater
95 percent confidence interval:

可以发现该检验的p值为0.556。这个p值太大，无法拒绝零假设，也就是说，没有理由认为两个班级认为有教学效果的人的比例有显著差异。

例题七

某调查机构调查某市低收入、中收入和高收入的居民对一项税收政策的支持率是否一致，分别调查了52名低收入居民、40名中等收入居民和31名高收入居民，其结果见表6-3。请判断这三种收入的 居民对这种税收政策的支持率是否一致。

首先在R中读取数据：

tax.policy=matrix(c(45,7,25,15,12,9),2)
colnames(tax.policy)=c("低收入","中等收入","高收入")
rownames(tax.policy)=c("支持","不支持")

这个检验计算每组的观测比例和所有组的比例之间的加权平方和的偏差。检验统计量近似服从自由度为k-1的χ2分布
为了在这样的数据集上使用prop.test()函数，需要提取每个收入等级的们支持政策或“成功”的数据，以及每个收入 等级的被调查人总数。这两个数据分别为：

tax.policy.yes=tax.policy［"支持",］#每个收入等级的支持数
tax.policy.total=margin.table(tax.policy,2)
#每个收入等级的被调查人总数#margin.table(mytable,1)对每一行的数据求和#margin.table(mytable, 2)对每一列的数据求和

然后就很容易进行检验了：

prop.test(tax.policy.yes,tax.policy.total)

3-sample test for equality of proportions without continuity

可以看出，这个检验的结果是显著的。
不同收入等级的人们对税收政策的支持情况是不一致的。
从支持率的点估计可以发现，收入等级越高，对税收政策的支 持率降低。
也可以使用prop.trend.test()来检验不同部分的趋势

prop.trend.test(tax.policy.yes,tax.policy.total)

---

总结

以上就是对方差分析的全部介绍。