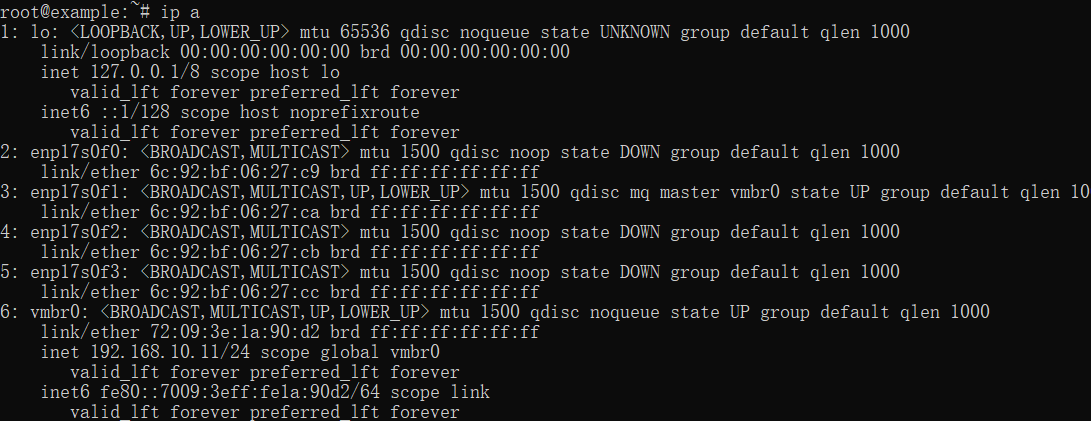
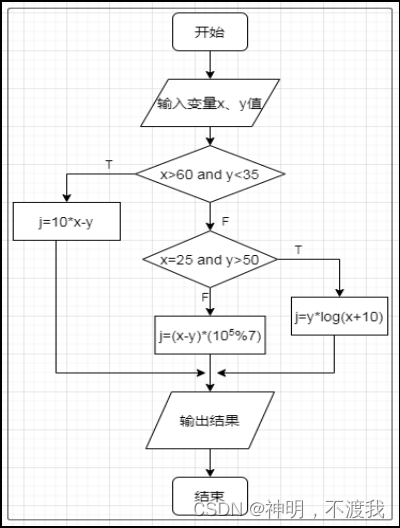
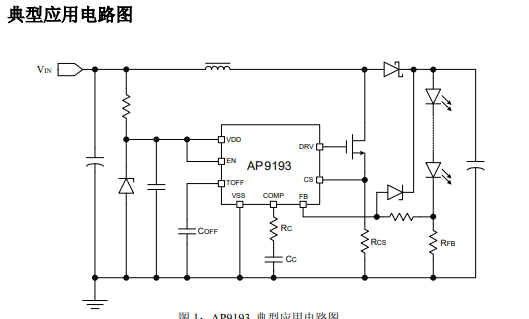
背景
工作领域是AI芯片工具链相关,很多相关知识的概念都是跟着项目成长建立起来,但是比较整个技术体系在脑海中都不太系统,比如项目参与中涉及到了很多AI编译器开发相关内容,东西比较零碎,工作中也没有太多时间去做复盘与查漏补缺。但是最近比较闲,发现了一个宝藏级的B站博主,系统的讲了很多AI芯片领域的知识,并把课程资源开源维护,极力推荐大家多多关注。在这里当个搬运工,传播一下。
总结
AI系统框架图及AI编译器前端的位置示意如下:
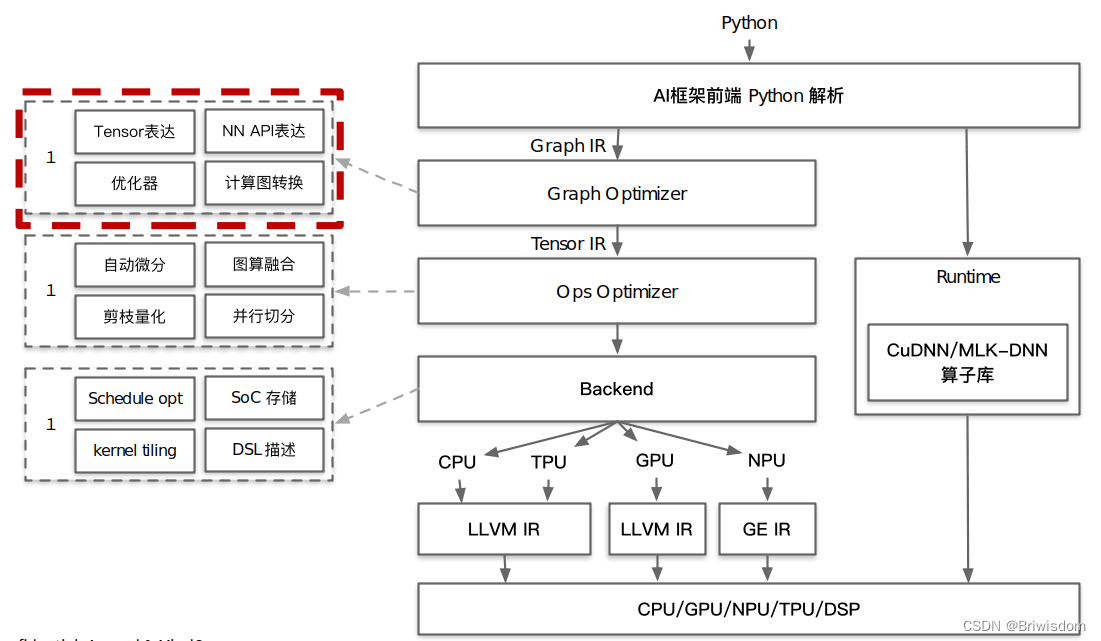
AI编译器的前端优化可以总结为神经网络相关的优化和代码/计算层面的优化两个方向。后面针对具体的点展开细说。

分述
图层IR
本节包含:
- 计算图构成
- 静态计算图和动态计算图
- 对AI编译器的作用

1)计算图的构成
- 用来表示深度学习网络模型在训练与推理过程中计算逻辑与状态
- AI框架在后端会将Python构建网络模型前向与反向梯度计算以计算图的形式来表示
- 由基本数据结构张量 (Tensor) 和基本运算单元算子 (Operator) 构成
- 计算图中常用节点来表示算子,节点间的有向线段来表示张量状态,同时也描述了
- 计算间的依赖关系
2) 静态计算图和动态计算图
静态图模式下:使用前端语言定义模型形成完整的程序表达后,不使用前端语言解释器进行执行,将前端描述的完整模型交给AI框架。AI框架先对API代码分析,获取网络层之间的连接拓扑
关系以及参数变量设置、损失函数等,接着用静态数据结构来描述拓扑结构及其他神经网络模
型组件。
动态图采用前端语言自身的解释器对代码进行解析,利用AI框架本身的算子分发功能,算子会即刻执行并输出结果。动态图模式采用用户友好的命令式编程范式,使用前端语言构建神经网
络模型更加简洁。
| 特性 | 静态图 | 动态图 |
|---|---|---|
| 即时获取中间结果 | 否 | 是 |
| 代码调试难易 | 难 | 简单 |
| 控制流实现方式 | 特定的语法 | 前端语言语法 |
| 性能 | 优化策略多,性能更佳 | 图优化受限,性能较差 |
| 内存占用 | 内存占用少 | 内存占用相对较多 |
| 部署能力 | 可直接部署 | 不可直接部署 |
动态图转换静态图的方式
• 基于追踪转换 :以动态图模式执行并记录调度的算子,构建和保存为静态图模型。
• 基于源码转换 :分析前端代码将动态图代码自动转为静态图代码,底层使用静态图执行运行。
3)计算图对AI编译器的作用
图优化
- 计算图的出现允许 AI 框架在执行前看到深度学习模型定义全局信息
- 计算图作为 AI 框架中的高层中间表示,可以通过图优化 Pass 去化简计算图或提高执行效率
图层IR的好处
方便底层编译优化
- 统一表示来描述神经网络训练的全过程
- 可以序列化保存,不需要再次编译前端源代码
- 将神经网络模型中间表示转换为不同硬件代码
- 直接部署在硬件上,提供高效的推理服务
- 编译期可对计算过程的数据依赖进行分析:
◦ 简化数据流图
◦ 动态和静态内存优化
◦ 预计算算子间的调度策略
◦ 改善运行时Runtime性能
分层优化,便于扩展
- 切分出三个解耦的优化层
◦ 计算图优化
◦ 运行时调度优化
◦ 算子/内核执行优化 - 新网络模型结构/新训练算法,扩展步骤: ◦ 计算图层添加新算子
◦ 针对不同硬件内核,实现计算优化
◦ 注册算子和内核函数,运行时派发硬件执行
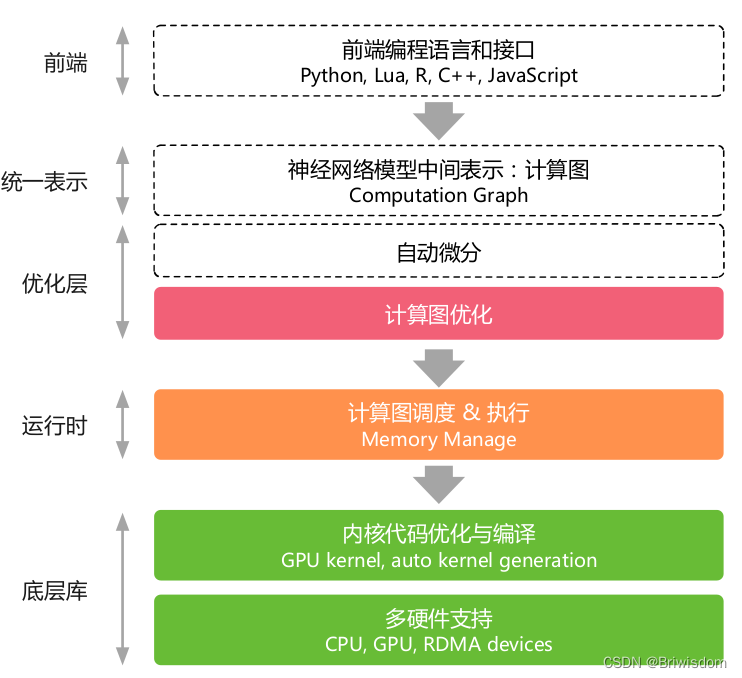
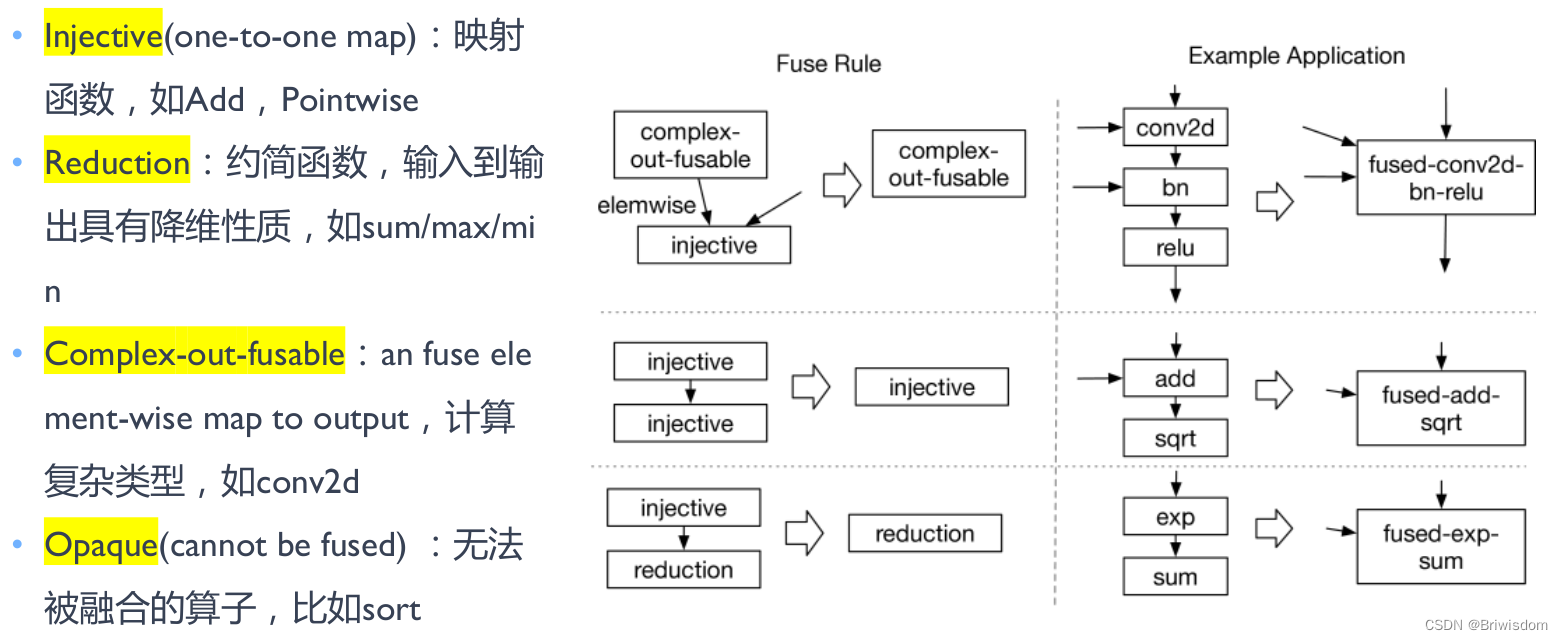
算子融合
本节包括:
- 算子融合方式
- 算子融合例子
- 融合的规则和算法
总结:
- 算子的融合方式有横向融合和纵向融合,但根据AI模型结构和算子的排列,可以衍生出更多不同的融合方式;
- 通过 Conv-BN算子融合示例,了解到如何对算子进行融合和融合后的计算,可以减少对于对访存的压力;
- 在编译器中,一般融合规则都是通过Pass来承载,不同的Pass处理不同的融合规则,而融合规则主要是人工定义好;
1)算子融合方式
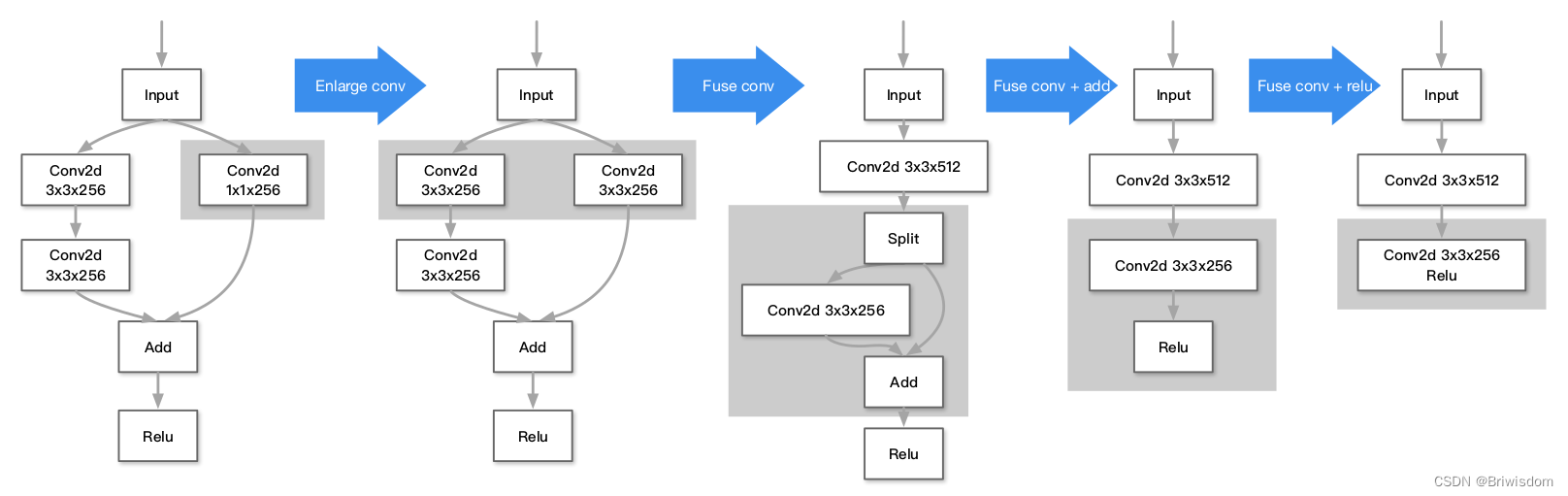
融合算子出现主要解决模型训练过程中的读入数据量,同时,减少中间结果的写回操作,降低访存操作。如下图是一个把原始的左边计算图,经过算子融合策略,变为最右边的计算图的过程。扩展过程:enlarge conv -》 fuse conv -》fuse conv+add -》fuse conv+add+relu
算子融合的要点:
- 消除不必要的中间结果实例化
- 减少不必要的输入扫描
- 发现其他优化机会
内存墙:主要是访存瓶颈引起。算子融合主要通过对计算图上存在数据依赖的“生产者-消费者
”算子进行融合,从而提升中间Tensor数据的访存局部性,以此来解决内存墙问题。这种融合技术也统称为“Buffer融合”。在很长一段时间,Buffer融合一直是算子融合的主流技术。早期的AI框架,主要通过手工方式实现固定Pattern的Buffer融合。
并行墙:主要是由于芯片多核增加与单算子多核并行度不匹配引起。可以将计算图中的算子节点进行并行编排,从而提升整体计算并行度。特别是对于网络中存在可并行的分支节点,这种
方式可以获得较好的并行加速效果。
2)conv+BN 的融合过程推导
卷积计算: z = w * x + b
BN计算:
合并推导:
在模型推理阶段,w, b, mean, var, ,
都已经固定下来了,所以令

可得:
3)融合规则与算法
TVM算子融合流程:
- 通过AST转换为Relay IR,遍历Relay IR;
- 建立DAG用于后支配树分析;
- 应用算子融合算法
流程展开:
1. 首先根据DAG进行深度优先遍历,生成DFS树,需要注意的是,DFS树是倒序,也就是最后一个节点是节点0,然后依次深度递增;除了单纯的记录每个Node的深度之外,我们还需要
为每个节点保存与他相连的边,注意这个边是与的父节点(也就是真正网络中他的输出节点
,倒序就变成了他的父节点了)组成的。之所以这里需要保存这个边和其对应的index,就是
为了后面找LCA用。
2. 根据DFS树及对应的边(link)生成DOM树,TVM是使用group这个概念来描述几个Node
能否融合,如果一个算子不能和任何其他算子融合,那么这个group就只有他自己,同样如果几个算子能够融合,产生一个新group。
3. 遍历每个Node到它的支配带你的所有路径是否符合融合规则,完成融合后,遍历节点创新
的DAG图
融合分类与示例:
布局转换
本节包括
- 数据内存排布
- 张量数据布局
- 编译布局转换优化
1)数据内存排布
内存对齐
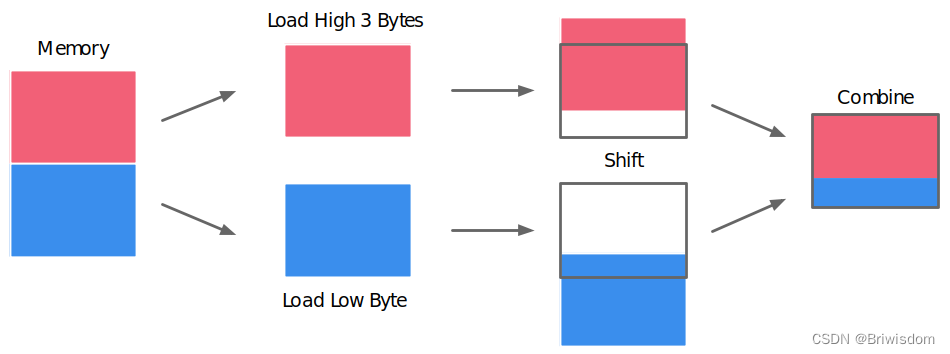
内存对齐和数据在内存中的位置有关。内存对齐以字节为单位进行,一个变量的内存地址如果正好等于它的长度的整数倍,则称为自然对齐。
尽管内存以字节为单位,现代处理器的内存子系统仅限于以字的大小的力度和对齐方式访问,处理器按照字节块的方式读取内存。一般按照2, 4,8, 16 字节为粒度进行内存读取。合理的内
存对齐可以高效的利用硬件性能。
以4字节存取粒度的处理器为例,读取一个int变量(32bit 系统), 处理器只能从4的倍数的地
址开始。假如没有内存对齐机制,将一个int放在地址为1的位置。现在读取该int时,需要两次
内存访问。第一次从0地址读取,剔除首个字节,第二次从4地址读取,只取首个字节;最后两
下的两块数据合并入寄存器,需要大量工作。
在AI芯片设计中,数据在处理器的排布和存取块的定义非常重要,而编译器则是要充分利用数据在内存的排布方式来使其达到高效的访存性能。
2)张量数据布局
Tensor 是一个多维数组,它是标量、向量、矩阵的高维拓展。标量是一个零维张量,没有方
向,是一个数。一维张量只有一个维度,是一行或者一列。二维张量是一个矩阵,有两个维度
,灰度图片就是一个二维张量。当图像是彩色图像(RGB)的时候,就得使用三维张量了。
对于二维张量,又有行优先和列优先排布方式。这个概念大家应该都比较熟悉了。尽管存储的数据实际上是一样的,但是不同的顺序会导致数据的访问特性不一致,因此即使进行同样的运算,相应的计算性能也会不一样。
在深度学习领域,多维数据通过多维数组存储,比如卷积神经网络的特征图(Feature Map)
通常用四维数组保存,即4D,4D格式解释如下:
N:Batch数量,例如图像的数目。
H:Height,特征图高度,即垂直高度方向的像素个数。
W:Width,特征图宽度,即水平宽度方向的像素个数。
C:Channels,特征图通道,例如彩色RGB图像的Channels为3。
NCHW
• NCHW 同一个通道的数据值连续排布,更适合需要对每个通道单独运算的操作,如 MaxPooling
• NCHW 计算时需要的存储更多,适合GPU运算,利用 GPU 内存带宽较大并且并行性强的特点
,其访存与计算的控制逻辑相对简单

NHWC
• NHWC 其不同通道中的同一位置元素顺序存储,因此更适合那些需要对不同通道的同一数据
做某种运算的操作,比如“Conv1x1”
• NHWC 更适合多核CPU运算,CPU 内存带宽相对较小,每个数据计算的时延较低,临时空间
也很小,有时计算机采取异步的方式边读边算来减小访存时间,因此计算控制灵活且复杂。

由于数据只能线性存储,因此这四个维度有对应的顺序。不同深度学习框架会按照不同的顺序存储特征图数据:
◦ 以 NPU/GPU 为基础的 PyTorch 和 MindSpore 框架默认使用 NCHW 格式,排列顺序为[Batch,
Channels, Height, Width]
◦ Tensorflow 采用了 NHWC,排列顺序为[Batch, Height, Width, Channels],何面向移动端部署
TFLite 只采用 NHWC 格式
一些专用处理器架构也会采用5D数据存储格式,如NHWC -> NC1HWC0, 其中C1= C/ C0,HWC0是一个处理数据块,可以根据处理器具体设计提高通用矩阵乘法(GEMM)运算数据块的访问效率。
3)AI编译器布局优化
目的:将内部数据布局转化为后端设备友好的形式
方式:试图找到在计算图中存储张量的最佳数据布局,然后将布局转换节点插入到图中
注意:张量数据布局对最终性能有很大的影响,而且转换操作也有很大的开销
NCHW 格式操作在 GPU 上通常运行得更快,所以在 GPU 上转换为 NCHW 格式是非常有效。一些 AI 编译器依赖于特定于硬件的库来实现更高的性能,而这些库可能需要特定的布局。此外,一些 AI 加速器更倾向于复杂的布局。边缘设备通常配备异构计算单元,不同的单元可能需要
不同的数据布局以更好地利用数据,因此布局转换需要仔细考虑。AI 编译器需要提供一种跨各
种硬件执行布局转换的方法。
对于训练场景的布局优化操作:
• 不改变原计算图
• 插入转换算子
• 取消转换算子
对于推理场景的布局优化操作:
• 不改变原计算图
• 插入转换算子
• 取消转换算子
• 权重布局转换
• 算子替换
内存分配
AI模型在训练时候需要占用大量的显存空间,现在在风口的大模型推理时候也有很大的内存需求。因此AI编译器的内存分配策略非常重要。使用AI编译器利用 Graph IR 可以巧妙和正确地分配内存。而运行深度学习推理的消耗比深度学习训练的内存消耗要少得多。
静态内存
• Parameter - 网络中的权重
• Value Node - 网络中的常量
• Output - 网络的输出
比如一些固定的算子在整个计算图中都会使用,此时需要再模型初始化时一次性申请完内存空间,在实际推理时不需要频繁申请操作,提高性能
动态内存
• Output Tensor - 网络中的算子的输出Tensor
• Workspace Tensor - 网络中的部分算子在计算过程中的临时buffer
动态内存分配:对于中间临时的内存需求,可以进行临时申请和释放,节省内存使用,提高模型并发能力
节省内存算法:
- 空间换内存:如卸载到CPU (CPU Offload )
- 计算换内存: 重计算 (Gradient Checkpointing)
- 模型压缩:如量化训练 Quantification, 剪枝等压缩算法
- 内存复用:利用AI编译器对计算图中的数据流进行分析,以允许重用内存
内存优化方法:
Inplace operation:如果一块内存不再需要,且下一个操作是element-wise,可以原地覆盖内存
Memory sharing:两个数据使用内存大小相同,且有一个数据参与计算后不再需要,后一个数据可以覆盖前一个数据
常量折叠
常量折叠和常量传播是编译器优化常用的技术,如下是它们的简单示例。
常量折叠

常量传播

AI编译器中的常量折叠是将计算图中可以预先可以确定输出值的节点替换成常量,并对计算图进行一些结构简化的操作。比如之前讲过的conv+BN,把conv的weight和BN的参数合并在一起,就达到了常量折叠的效果。
 ============》
============》 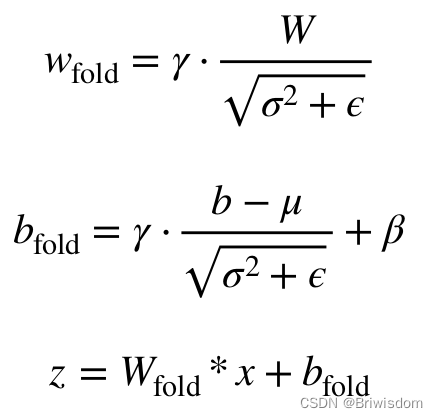
分类
- 传统编译器中的常量折叠,找到输入节点均为常量的节点,提前计算出该节点的值来完整替换该节点。
- 常量折叠与数据形状 shape 有关系,通过计算图已有信息推断出形状结果后,用来代替原来的节点。
- 常量折叠与已知常量的代数化简有关。
TensorFlow 常量折叠 PASS
- 先处理“Shape”, “Size”, “Rank”三类运算节点,其输出都取决与输入Tensor的形状,而与具体的输入取值没关系,所以输出可能是可以提前计算出来的。
- 把“Shape”, “Size”, “Rank”上述三类运算节点,提前计算出输出值替换成 Const 节点,目的是方便后续的常量折叠和替换。
- 折叠计算图操作:如果一个节点的输入都是常量,那么它的输出也是可以提前计算的,基于这个原理不断地用常量节点替换计算图中的此类节点,直到没有任何可以替换的节点为止。
- 处理 Sum, Prod, Min, Max, Mean, Any, All 这几类运算节点,这几类节点的共同点是都沿着输入Tensor的一定维度做一定的运算,或是求和或是求平均等等,将符合一定条件的这几类节点替换为 Identity 节点。
公共子表达式消除
CSE(Common subexpression elimination),是一个编译器优化技术。在执行这项优化的过程中,编译器会视情况将多个相同的表达式替换成一个变量,这个变量存储着计算该表达式后所得到的值。
如下示例,可以观察到 𝑏 ∗ 𝑐 是两项表达式中的公共子表达式。如果计算这个子表达式并将其计算结果存储起来的开销,低于重复计算这个子表达式的开销,就可以执行公共表达式消除的优化操作。
 ====》
====》 
编译器开发者将公共子表达式消除分成两种:
- 本地公共子表达式消除:这项优化技术工作于基本块之内。
- 全局公共子表达式消除:这项优化技术工作于整个过程之中。
AI 编译器中公共子表达式消除采取相同的思路,区别在于AI编译器中子表达式是基于计算图或者图层 IR。通过在计算图中搜索相同结构的子图,简化计算图的结构,从而减少计算开销。
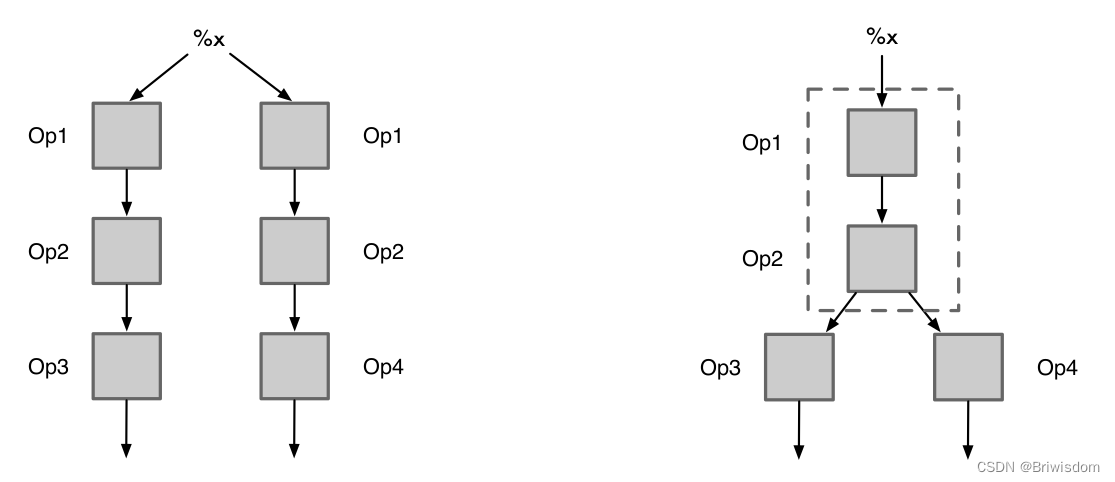
原则
• 通过建立候选哈希表 MAP, 记录已处理过的同一种类型的 OP。对于当前正在处理的 OP,先查找该 MAP 表,如果能找到其他和正在处理的 OP 类型相同的 OP,则对其进行遍历,如果其中某个 OP 的输入和参数与当前正在处理的 OP 相同,则它们为公共子表达式,结果可以互相替
代;如果所有 OP 都不能与当前正在处理的 OP 匹配,则将当前 OP 复制一份回。
算法
输入:计算图 Graph IR,找到公共子表达式并优化计算图:
- 获取逆后续节点集 Set(Reverse):对计算图 Graph IR 进行深度优先遍历 DFS,将结果逆转得到逆后续节点集。逆后续得到的结果就是拓扑排序,即访问到某一个节点时,该节点的依赖节点都已经被访问。
- 创建 Map(MSE):存储公共子表达式候选集,遍历 Set(Reverse) 时,可以从候选集 Map(MSE) 中查找是否有可以使用的表达式。
- 遍历计算图的所有节点,判断是否有公共子表达式:获取节点 hash 值,hash的 key 由输出个数 + 输出类型s + 输入节点 id,key 可以保证输入相同及输出个数和类型相同时,得到的hash值相同,达到检索公共表达式的目的。
- 记录入候选集:根据 hash 值 h 从 Map(MSE) 中得到候选集,当候选集为空,第一次遇到这样的表达式,将节点 Node 存入 Map(MSE) 中。
- 可复用公共子表达式判断 :C andidate 非空,则说明之前遍历到了相似的表达式,进一步判断是否可复用已保存节点表达式的结果。即节点的输入都是来自相同的Const节点,可以保证输入数据完全相同;输出个数和类型相同,可以保证输出的结果相同;满足条件下,可复用之前保存节点的结果,不用再次进行计算。
- 删除重复节点:判断表达式可以复用后,最后一步就是删除重复的节点,将 Candidate 的输出连接到当前节点的输出节点对应的输入,最后删除当前节点。
死代码消除
概念
编译器原理中,死码消除(Dead code elimination)是一种编译优化技术,它的用途是移除对程序执行结果没有任何影响的代码。移除这类的代码有两种优点,不但可以减少程序的大小,还
可以避免程序在执行中进行不相关的运算行为,减少它执行的时间。

原则
• 死代码消除可以优化计算图的计算和存储效率,避免为死节点(无用节点)分配存储和进行计算,同时简化了计算图的结构,方便进行后续的其他图优化Pass。
• 死代码消除一般不是在定义神经网络模型结构时候引起的,而是其他图优化 Pass 造成的结果,因此死代码消除 Pass 常常在其他图优化 Pass 后被应用。
示例
• 死代码消除一般不是在定义神经网络模型结构时候引起的,而是其他图优化 Pass 造成的结果,因此死代码消除 Pass 常常在其他图优化 Pass 后被应用。如无用的控制流、推理时删除仅训练相关的子图。
算法
输入:计算图 Graph IR,找到死节点(无用节点)并优化计算图。
- 获取逆后续节点集 Set(Reverse):对计算图 Graph IR 进行深度优先遍历 DFS,将结果逆转得到逆后续节点集。逆后续得到的结果就是拓扑排序,即访问到某一个节点时,该节点的依赖节点都已经被访问。
- 遍历后续节点集 ,判断是否为死节点:获取节点的输出值,判断是否为计算图的输出节点;如果不是输出节点且无对应输出节点,则为死节点。
- 删除死节点,从新遍历计算图:删除死节点,值得注意的是死节点删除后需要删除对应输入的边。然后重复步骤1。
代数化简
原则
• 代数化简的目的是利用交换率、结合律等规律调整图中算子的执行顺序,或者删除不必要的算
子,以提高图整体的计算效率。
算法
代数化简可以通过子图替换的方式完成,具体实现:
• 可以先抽象出一套通用的子图替换框架,再对各规则实例化。
• 可以针对每一个具体的规则实现专门的优化逻辑。
示例
结合律化简:
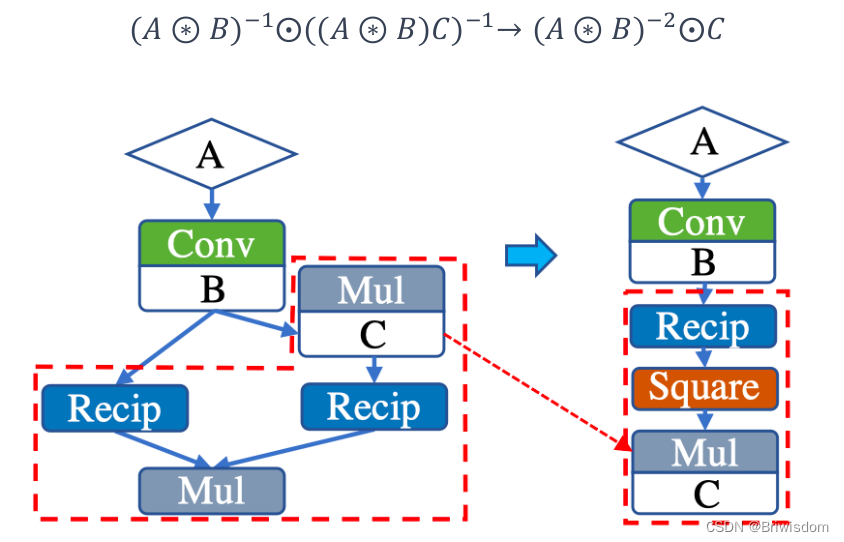
提取公因式、分配律化简:

交换律化简:
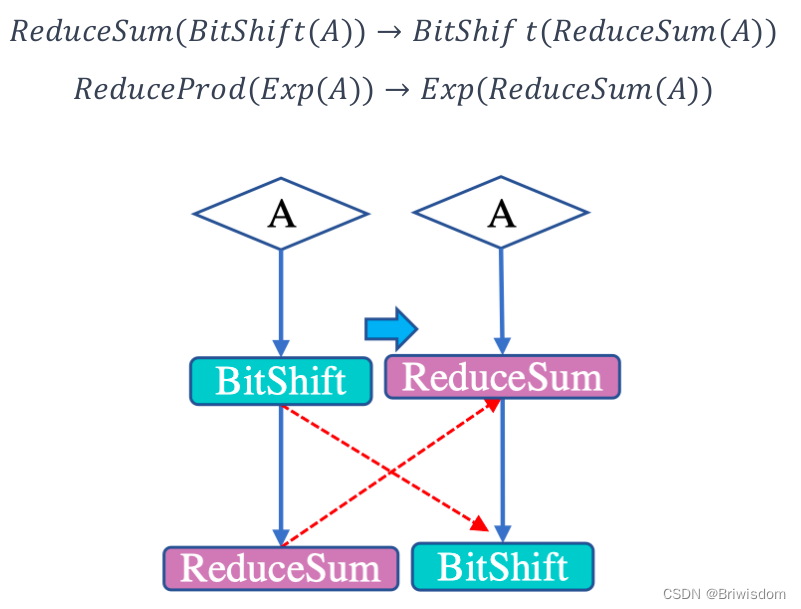
运行化简:
- 对逆函数等于自身函数的对合算子化简,如取反、倒数、逻辑非、矩阵转置

- 幂等算子化简,作用在某一元素两次与一次相同

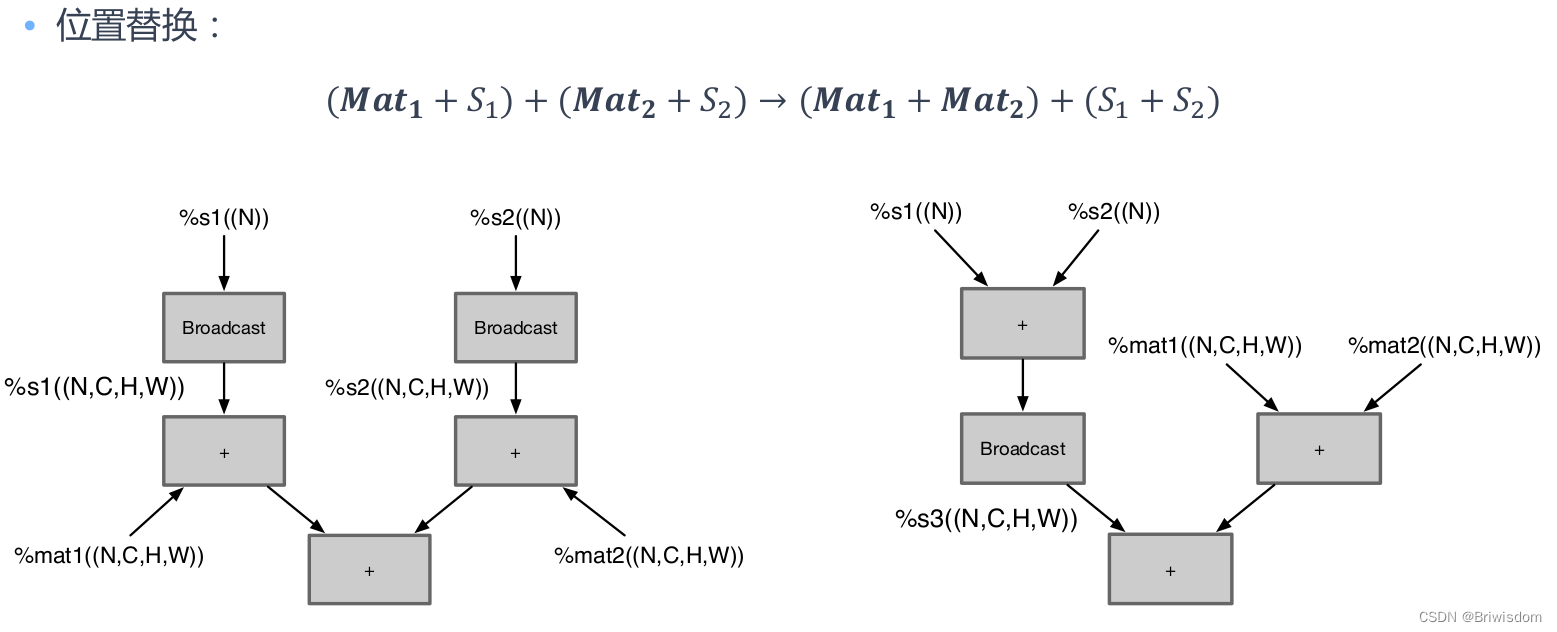
广播化简:
- 多个张量形状 Shape 不同,需要进行广播将张量的形状拓展为相同 shape 再进行运算,化简为最小计算所需的广播运算数量。
系列:AI编译器的后端优化策略-CSDN博客