线性代数之行列式
行列式的几条重要的性质
1.某两行某两列交换位置之后,值变号
2.行列式转置,值不变
3.范德蒙德行列式,用不同行的公比做一系列的累乘运算
4.把某一行的行列式加到另一行上,利用他们之间的倍数关系,转化成上三角行列式,利用对角线乘积得出行列式的值
5.当行列式的某一行有公共因子的时候,可以提供因子,但是一次只能提一个,否则会出现错误

6.行列式的某行或某列相等,或者成比例行列式的值为零
7.
通过观察可以发现,该行列式的第二行可能是某一行的整数倍,这个时候我们就要注意观察第三行,第四行的和,利用行列式的性质简化运算。
8.当行列式的某一项是几个代数式的和时,可以拆开进行运算,但是一次也只能拆一个,同时要注意行列式的某行或某列未被调换位置,导致行列式的值变成对应的相反数
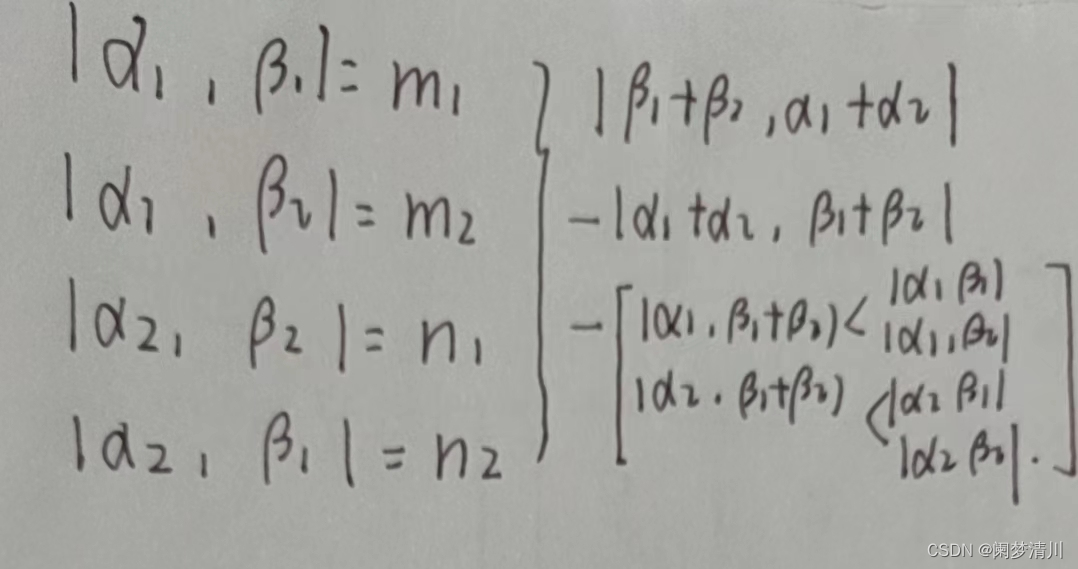
9.行列式的展开,行列式等于它的任意一行或者任意一列的元素和其对应的代数余子式的乘积之和。
10.如果某一列的行列式的元素加起来的值相同,这个时候,我们把所有行或者所有列相加到同一行或者同一列,然后再把第一行或者第一列提取公因数变成一,转化为上三角行列式进行计算。
11.在利用代数余子式进行行列式展开时,行列式的阶数可能会发生变化,这个时候要关注行列式的阶数变化的具体情况来进行正确的计算