MATLAB - 仿真单摆的周期性摆动

系列文章目录

前言

本例演示如何使用 Symbolic Math Toolbox™ 模拟单摆的运动。推导摆的运动方程，然后对小角度进行分析求解，对任意角度进行数值求解。

一、步骤 1：推导运动方程

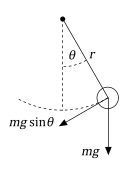
摆是一个遵循微分方程的简单机械系统。摆最初静止在垂直位置。当摆移动一个角度 θ 并释放时，重力将其拉回静止位置。它的动量会使它过冲并到达 -θ 角（如果没有摩擦力），以此类推。由于重力的作用，钟摆运动的恢复力为 -mgsinθ。因此，根据牛顿第二定律，质量乘以加速度必须等于 -mgsinθ。

syms m a g theta(t)
eqn = m*a == -m*g*sin(theta)

eqn(t) = a m=−g m sin(θ(t))

对于长度为 r 的摆锤，摆锤的加速度等于角加速度乘以 r。

$eq?a%3Dr%5Cfrac%7Bd%5E2%5Ctheta%7D%7Bdt%5E2%7D.$

用子项代替 a。

syms r
eqn = subs(eqn,a,r*diff(theta,2))

$eq?%5Cbegin%7Baligned%7Deqn%28t%29%26%3D%5C%5Cmr%5Cfrac%7B%5Cpartial%5E2%7D%7B%5Cpartial%20t%5E2%7D%26%5Ctheta%28t%29%3D-gm%5Csin%28%5Ctheta%28t%29%29%5Cend%7Baligned%7D$

使用 isolate 隔离公式中的角加速度。

eqn = isolate(eqn,diff(theta,2))

$eq?%5Cbegin%7Baligned%7D%5Ctext%7Beqn%20%3D%7D%20%5Cfrac%7B%5Cpartial%5E2%7D%7B%5Cpartial%20t%5E2%7D%5Cleft.%5Ctheta%28t%29%3D-%5Cfrac%7Bg%5Csin%28%5Ctheta%28t%29%29%7Dr%5Cright.%5Cend%7Baligned%7D$

将常数 g 和 r 合并为一个参数，也称为固有频率。

$eq?%5Comega_0%3D%5Csqrt%7B%5Cdfrac%7Bg%7D%7Br%7D%7D.$

syms omega_0
eqn = subs(eqn,g/r,omega_0^2)

$eq?%5Cbegin%7Baligned%7D%5Ctext%7Beqn%20%3D%7D%5Cfrac%7B%5Cpartial%5E2%7D%7B%5Cpartial%20t%5E2%7D%5Ctheta%28t%29%3D-%5Comega_0%5E2%5Csin%28%5Ctheta%28t%29%29%5Cend%7Baligned%7D$

二、步骤 2：运动方程线性化

运动方程是非线性的，因此难以用解析法求解。假设角度很小，利用 sinθ 的泰勒展开式将方程线性化。

syms x
approx = taylor(sin(x),x,'Order',2);
approx = subs(approx,x,theta(t))

$eq?approx%20%3D%20%5Ctheta%28t%29$

运动方程变成了线性方程。

eqnLinear = subs(eqn,sin(theta(t)),approx)

$eq?%5Cbegin%7Baligned%7D%5Ctext%7BeqnLinear%7D%26%3D%5C%5C%5Cfrac%7B%5Cpartial%5E2%7D%7B%5Cpartial%20t%5E2%7D%5Ctheta%28t%29%26%3D-%5Comega_0%5E2%5Ctheta%28t%29%5Cend%7Baligned%7D$

三、步骤 3：分析求解运动方程

使用 dsolve 求解方程 eqnLinear。将初始条件指定为第二个参数。使用 assume 假设 ω0 为实数，简化解法。

syms theta_0 theta_t0
theta_t = diff(theta);
cond = [theta(0) == theta_0, theta_t(0) == theta_t0];
assume(omega_0,'real')
thetaSol(t) = dsolve(eqnLinear,cond)

$eq?%5Cbegin%7Baligned%7D%5Ctext%7Bthetasol%28t%29%7D%26%3D%5Ctheta_0%5Ccos%28%5Comega_0t%29+%5Cfrac%7B%5Ctheta_%7Bt0%7D%5Csin%28%5Comega_0t%29%7D%7B%5Comega_0%7D%5Cend%7Baligned%7D$

四、步骤 4：ω0 的物理意义

项 ω 0 t 称为相位。余弦函数和正弦函数每 2π 重复一次。改变 ω 0 t 变化 2π 所需的时间称为时间周期。

$eq?T%3D%5Cdfrac%7B2%5Cpi%7D%7B%5Comega0%7D%3D2%5Cpi%5Csqrt%7B%5Cdfrac%7Br%7D%7Bg%7D%7D.$

时间周期 T 与摆长的平方根成正比，与质量无关。对于线性运动方程，时间周期与初始条件无关。

五、步骤 5：绘制摆的运动图

绘制小角度近似的摆运动图。

定义物理参数：

重力加速度 $s%7D%5E%7B2%7D$
摆长 $eq?%5Ctext%7Br%3D1%20m%7D$

gValue = 9.81;
rValue = 1;
omega_0Value = sqrt(gValue/rValue);
T = 2*pi/omega_0Value;

设置初始条件。

theta_0Value  = 0.1*pi; % Solution only valid for small angles.
theta_t0Value = 0;      % Initially at rest.

将物理参数和初始条件代入一般解法。

vars   = [omega_0      theta_0      theta_t0];
values = [omega_0Value theta_0Value theta_t0Value];
thetaSolPlot = subs(thetaSol,vars,values);

绘制谐摆运动图。

fplot(thetaSolPlot(t*T)/pi, [0 5]);
grid on;
title('Harmonic Pendulum Motion');
xlabel('t/T');
ylabel('\theta/\pi');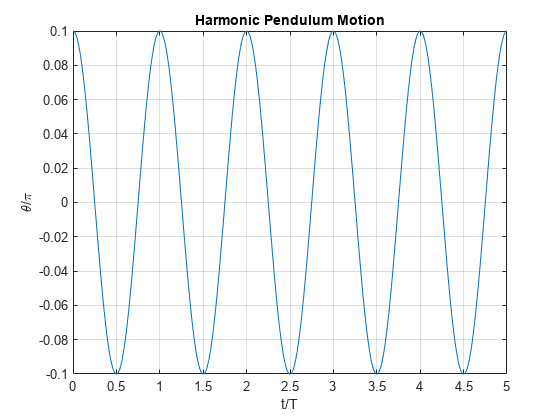

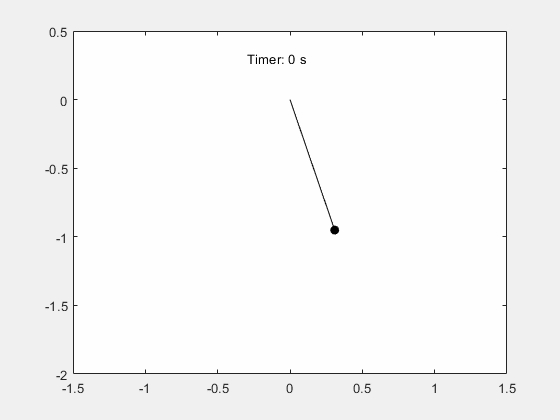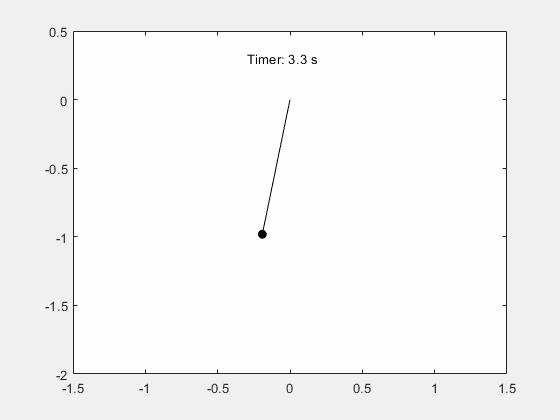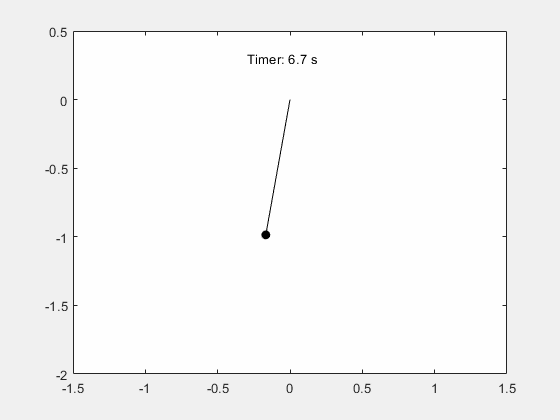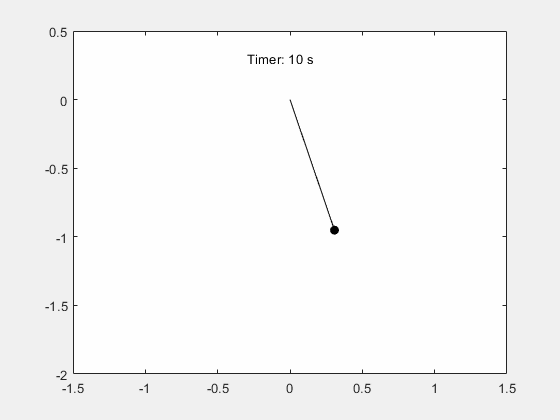
求出 θ(t) 的解后，想象一下摆的运动。

x_pos = sin(thetaSolPlot);
y_pos = -cos(thetaSolPlot);
fanimator(@fplot,x_pos,y_pos,'ko','MarkerFaceColor','k','AnimationRange',[0 5*T]);
hold on;
fanimator(@(t) plot([0 x_pos(t)],[0 y_pos(t)],'k-'),'AnimationRange',[0 5*T]);
fanimator(@(t) text(-0.3,0.3,"Timer: "+num2str(t,2)+" s"),'AnimationRange',[0 5*T]);

输入 playAnimation 命令播放钟摆运动的动画。

六、步骤 6：使用恒定能量路径确定非线性摆运动

为了理解摆的非线性运动，请使用总能量方程来直观显示摆的运动轨迹。总能量是守恒的。

$eq?E%3D%5Cdfrac12mr%5E2%7B%5Cleft%28%5Cdfrac%7Bd%5Ctheta%7D%7Bdt%7D%5Cright%29%7D%5E2+mgr%281-%5Ccos%5Ctheta%29$

使用三角函数特性 $2%29$ 和关系式 $r%7D$ 重写比例能量。

$eq?%5Cdfrac%20E%7Bmr%5E2%7D%3D%5Cdfrac12%5Cleft%5B%5Cleft%28%5Cdfrac%7Bd%5Ctheta%7D%7Bdt%7D%5Cright%29%5E2+%5Cleft%282%5Comega_0%5Csin%5Cdfrac%5Ctheta2%5Cright%29%5E2%5Cright%5D$

由于能量守恒，摆的运动可以用相空间中的恒定能量路径来描述。相空间是一个抽象空间，坐标为 θ 和 dθ/dt。使用 fcontour 将这些路径可视化。

syms theta theta_t omega_0
E(theta, theta_t, omega_0) = (1/2)*(theta_t^2+(2*omega_0*sin(theta/2))^2);
Eplot(theta, theta_t) = subs(E,omega_0,omega_0Value);figure;
fc = fcontour(Eplot(pi*theta, 2*omega_0Value*theta_t), 2*[-1 1 -1 1], ...'LineWidth', 2, 'LevelList', 0:5:50, 'MeshDensity', 1+2^8);
grid on;
title('Constant Energy Contours in Phase Space ( \theta vs. \theta_t )');
xlabel('\theta/\pi');
ylabel('\theta_t/2\omega_0');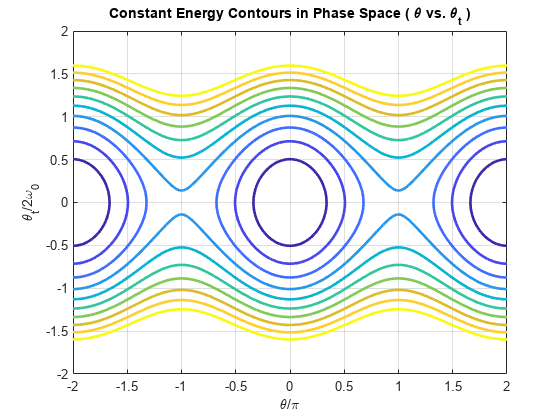

恒定能量等值线围绕 θ 轴和 dθ/dt 轴对称，沿 θ 轴呈周期性分布。图中显示了两个行为截然不同的区域。

等值线图的较低能量相互靠近。摆锤在两个最大角度和速度之间来回摆动。摆锤的动能不足以克服重力能，使摆锤绕一圈。

等值线图中的高能量不会自行闭合。摆锤始终沿着一个角度方向运动。钟摆的动能足以克服重力能，使钟摆能够绕一圈。

七、步骤 7：求解非线性运动方程

非线性运动方程是二阶微分方程。使用 ode45 求解器对这些方程进行数值求解。由于 ode45 只接受一阶系统，因此请将系统简化为一阶系统。然后生成函数句柄，作为 ode45 的输入。

将二阶 ODE 重写为一阶 ODE 系统。

syms theta(t) theta_t(t) omega_0
eqs = [diff(theta)   == theta_t;diff(theta_t) == -omega_0^2*sin(theta)]

$eq?%5Cleft.%5Ctext%7Beqs%7D%28t%29%3D%5C%5C%5Cleft%28%5Cbegin%7Baligned%7D%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20t%7D%26%5Ctheta%28t%29%3D%5Ctheta_t%28t%29%5C%5C%5C%5C%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%20t%7D%26%5Ctheta_t%28t%29%3D-%5Comega_0%5E2%5Csin%28%5Ctheta%28t%29%29%5Cend%7Baligned%7D%5Cright.%5Cright%29$

eqs  = subs(eqs,omega_0,omega_0Value);
vars = [theta, theta_t];

求出系统的质量矩阵 M 和方程 F 的右边。

[M,F] = massMatrixForm(eqs,vars)

$eq?%5Cbegin%7Barray%7D%7Brcl%7D%5Ctext%7BM%7D%26%3D%26%5C%5C%26%26%5Cbegin%7Bbmatrix%7D1%260%5C%5C0%261%5Cend%7Bbmatrix%7D%5Cend%7Barray%7D$

$eq?%5Cbegin%7Baligned%7D%7BF%7D%26%3D%5C%5C%26%5Cbegin%7Bbmatrix%7D%5Ctheta_t%28t%29%5C%5C-%5Cdfrac%7B981%5Csin%28%5Ctheta%28t%29%29%7D%7B100%7D%5Cend%7Bbmatrix%7D%5Cend%7Baligned%7D$

M 和 F 指的就是这种形式。

$eq?M%28t%2Cx%28t%29%29%5Cdfrac%7Bdx%7D%7Bdt%7D%3DF%28t%2Cx%28t%29%29.$

为简化进一步计算，可将系统改写为 $dt%3Df%28t%2Cx%28t%29%29.$ 的形式。

f = M\F

$eq?%5Cbegin%7Baligned%7D%5Ctext%7Bf%7D%26%3D%5C%5C%26%5Cbegin%7Bbmatrix%7D%5Ctheta_t%28t%29%5C%5C-%5Cdfrac%7B981%5Csin%28%5Ctheta%28t%29%29%7D%7B100%7D%5Cend%7Bbmatrix%7D%5Cend%7Baligned%7D$

使用 odeFunction 将 f 转换为 MATLAB 函数句柄。生成的函数句柄是 MATLAB ODE 求解器 ode45 的输入。

f = odeFunction(f, vars)

f = function_handle with value:@(t,in2)[in2(2,:);sin(in2(1,:)).*(-9.81e+2./1.0e+2)]

八、步骤 8：求解封闭能量等值线的运动方程

使用 ode45 求解封闭能量等值线的 ODE。

从能量等值线图来看，封闭等值线满足条件 $2%5Comega_0%5Cleq1$ . 将 θ 和 dθ/dt 的初始条件存储在变量 x0 中。

x0 = [0; 1.99*omega_0Value];

指定一个从 0 秒到 10 秒的时间间隔，用于求解。这个时间间隔允许摆锤经历两个完整的周期。

tInit  = 0;
tFinal = 10;

求解 ODE。

sols = ode45(f,[tInit tFinal],x0)

sols = struct with fields:solver: 'ode45'extdata: [1x1 struct]x: [0 3.2241e-05 1.9344e-04 9.9946e-04 0.0050 0.0252 0.1259 0.3449 0.6020 0.8591 1.1161 1.3597 1.5996 1.8995 2.2274 2.4651 2.7028 2.9567 3.2138 3.4709 3.7150 3.9511 4.2483 4.5759 4.8239 5.0719 5.3182 5.5764 5.8346 6.0803 ... ] (1x45 double)y: [2x45 double]stats: [1x1 struct]idata: [1x1 struct]

sols.y(1,:) 表示角位移 θ，sols.y(2,:) 表示角速度 dθ/dt。

绘制闭合路径解。

figure;yyaxis left;
plot(sols.x, sols.y(1,:), '-o');
ylabel('\theta (rad)');yyaxis right;
plot(sols.x, sols.y(2,:), '-o');
ylabel('\theta_t (rad/s)');grid on;
title('Closed Path in Phase Space');
xlabel('t (s)');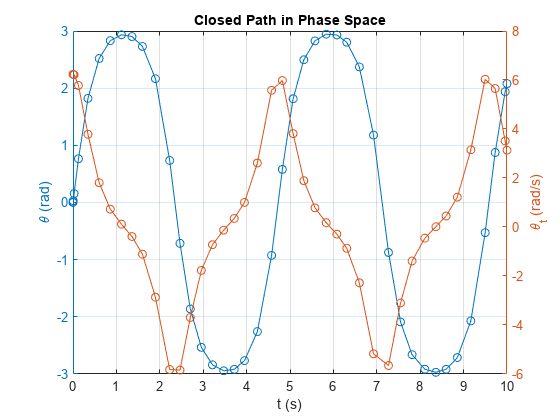

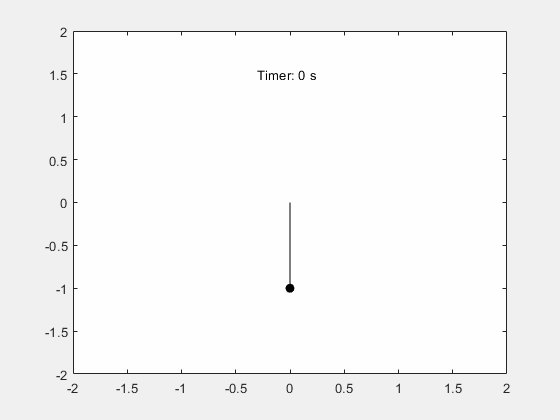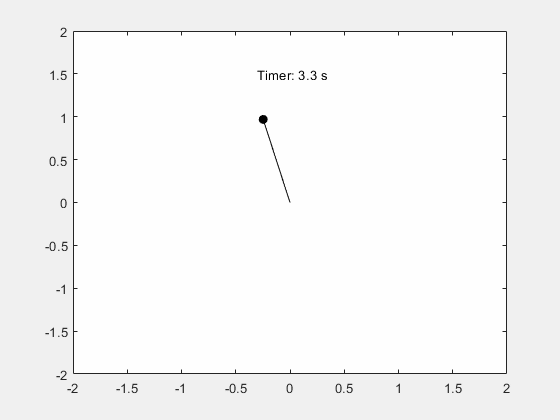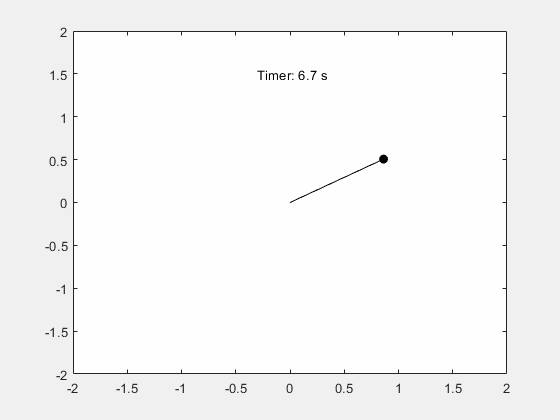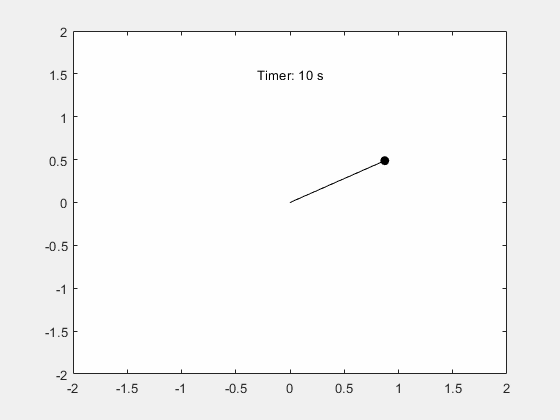
可视化钟摆的运动。

x_pos = @(t) sin(deval(sols,t,1));
y_pos = @(t) -cos(deval(sols,t,1));
figure;
fanimator(@(t) plot(x_pos(t),y_pos(t),'ko','MarkerFaceColor','k'));
hold on;
fanimator(@(t) plot([0 x_pos(t)],[0 y_pos(t)],'k-'));
fanimator(@(t) text(-0.3,1.5,"Timer: "+num2str(t,2)+" s"));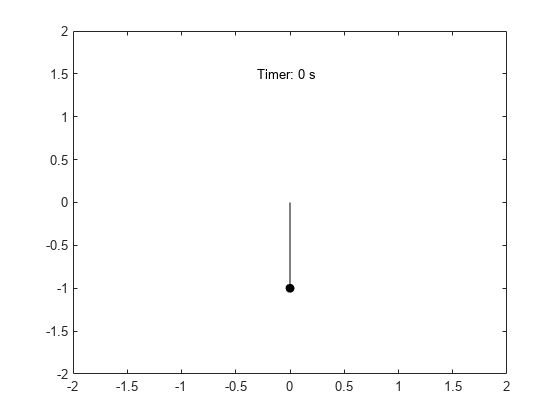

输入 playAnimation 命令播放钟摆运动的动画。

九、步骤 9：开放式能量等值线的求解

使用 ode45 求解开放式能量等值线的 ODE。从能量等值线图来看，开放式等值线满足条件 $2%5Comega_0%3E1.$ .

x0 = [0; 2.01*omega_0Value];
sols = ode45(f, [tInit, tFinal], x0);

绘制开放式能量等值线的解。

figure;yyaxis left;
plot(sols.x, sols.y(1,:), '-o');
ylabel('\theta (rad)');yyaxis right;
plot(sols.x, sols.y(2,:), '-o');
ylabel('\theta_t (rad/s)');grid on;
title('Open Path in Phase Space');
xlabel('t (s)');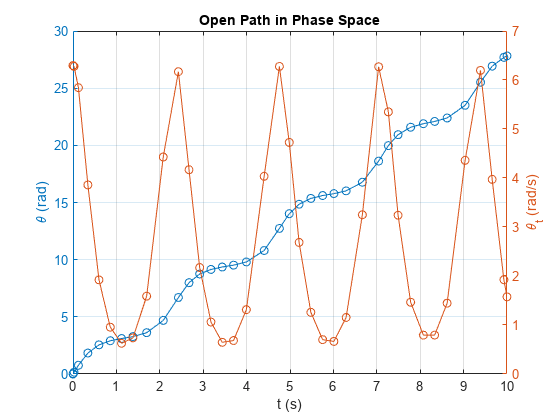

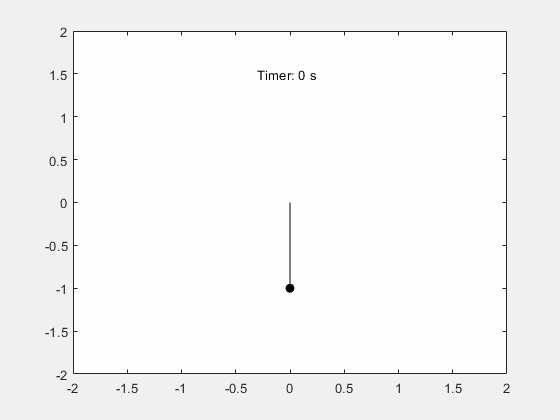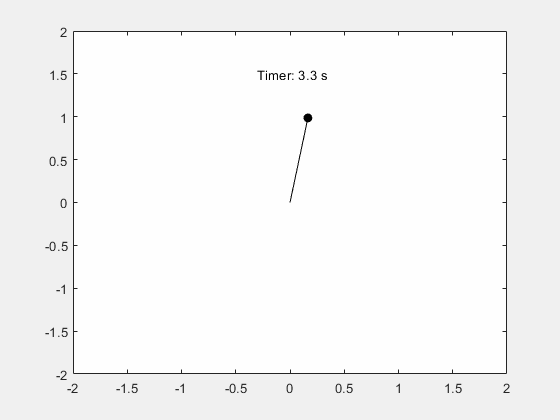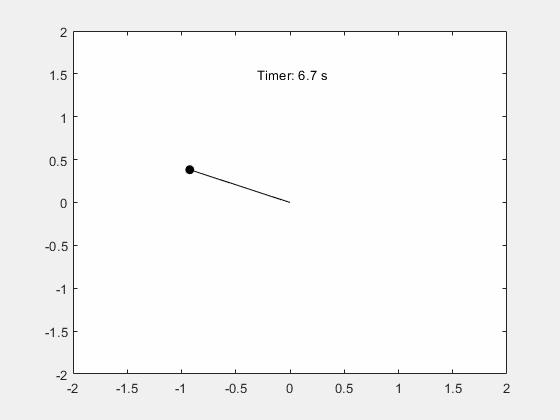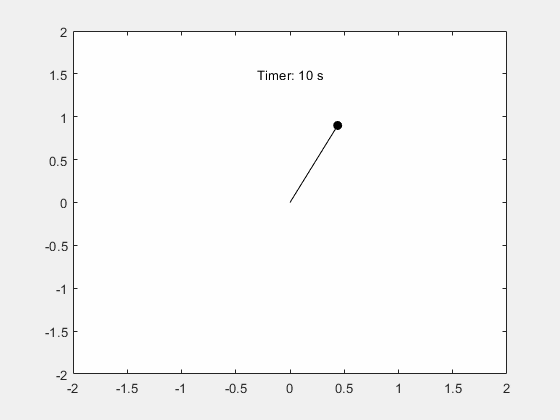
可视化钟摆的运动。

x_pos = @(t) sin(deval(sols,t,1));
y_pos = @(t) -cos(deval(sols,t,1));
figure;
fanimator(@(t) plot(x_pos(t),y_pos(t),'ko','MarkerFaceColor','k'));
hold on;
fanimator(@(t) plot([0 x_pos(t)],[0 y_pos(t)],'k-'));
fanimator(@(t) text(-0.3,1.5,"Timer: "+num2str(t,2)+" s"));