微分几何——梅向明第四版学习笔记（一） 向量函数和曲线论

在这里插入图片描述

目录

  • 引出
  • 向量函数
  • 曲线论
    • 简单曲线定义
      • 曲线的向量参数表示
    • 曲线的切线【重要】
    • 曲线的法面【重要】
    • 曲线的自然参数表示
  • 空间曲线
    • 曲线的密切平面
    • 空间曲线的基本三棱形【重要】
      • 单位切向量
      • 主法向量
      • 副法向量
      • Frenet标架
      • 螺旋线的案例
    • 曲线的曲率和曲率半径
      • 曲率的几何意义
    • 曲线的挠率
      • 挠率的几何意义
    • 空间曲线在一点邻近的结构
    • 空间曲线论基本定理
      • 一般螺旋线
  • 总结

引出

微分几何——梅向明第四版学习笔记（一） & 向量函数和曲线论

向量函数

向量函数定义及其表示方式

在这里插入图片描述
在这里插入图片描述

k次可微函数

在这里插入图片描述

向量函数的泰勒公式

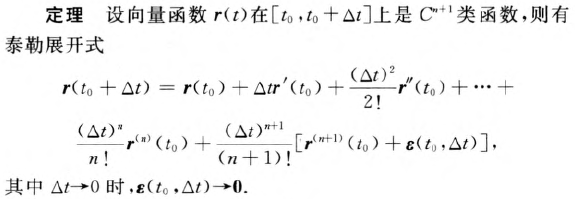
在这里插入图片描述

曲线论

简单曲线定义

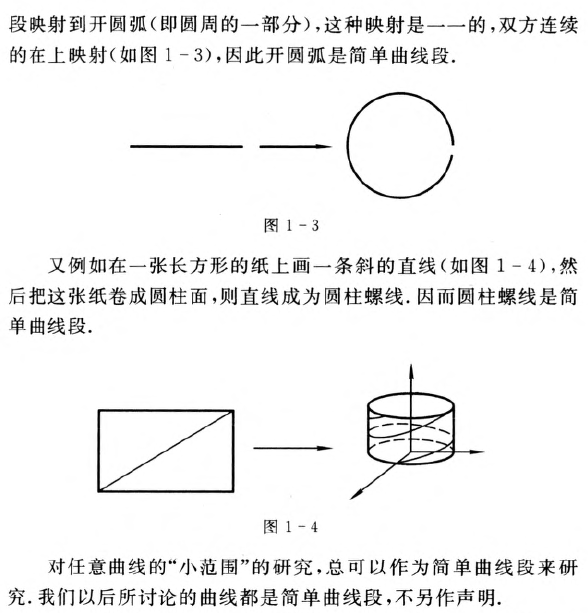
在这里插入图片描述

在这里插入图片描述

曲线的参数方程

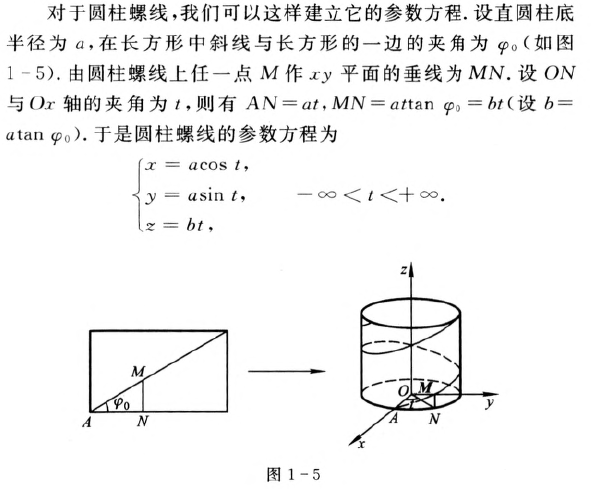
在这里插入图片描述

在这里插入图片描述

曲线的向量参数表示

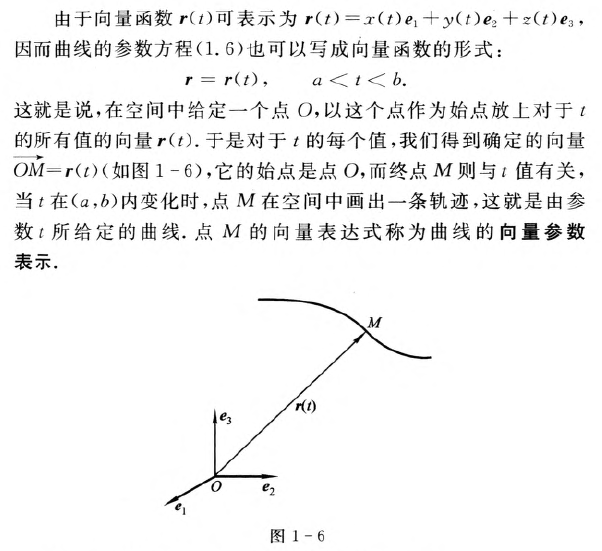
在这里插入图片描述

案例：

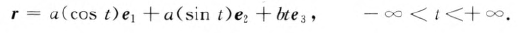
在这里插入图片描述

在这里插入图片描述

曲线的切线【重要】

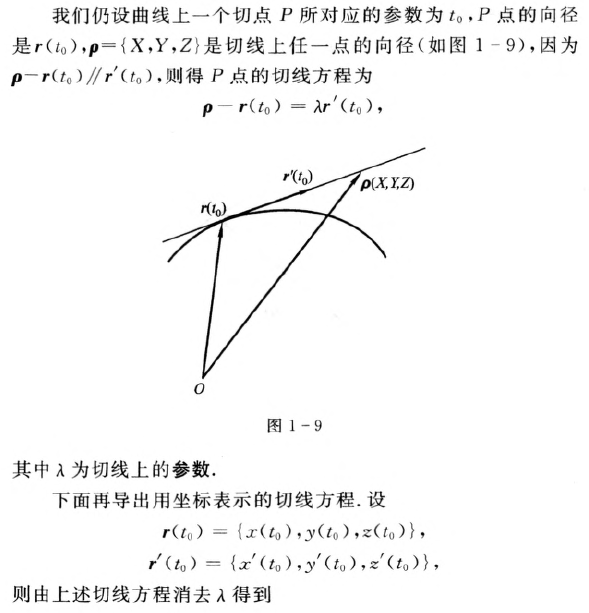
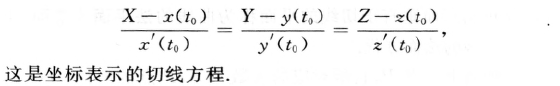
在这里插入图片描述

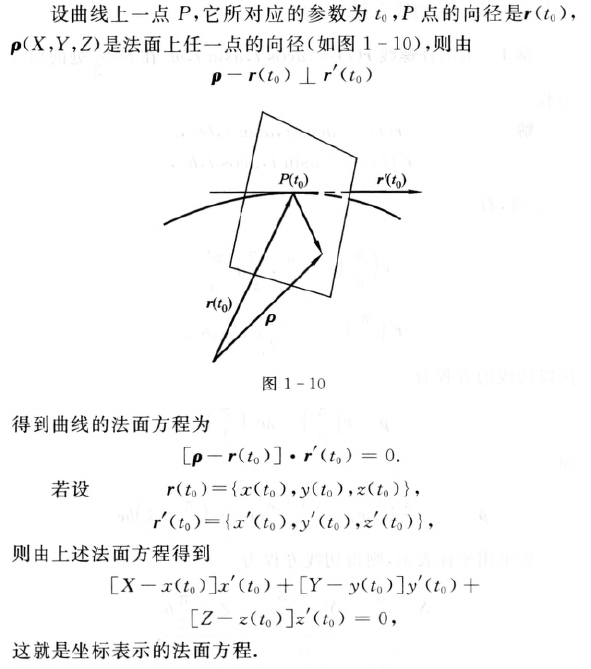
在这里插入图片描述

案例：

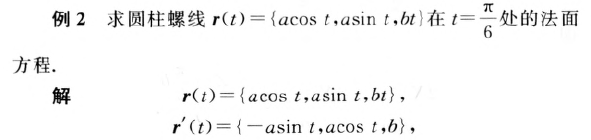
在这里插入图片描述

曲线的法面【重要】

在这里插入图片描述

案例：

在这里插入图片描述

在这里插入图片描述

曲线的自然参数表示

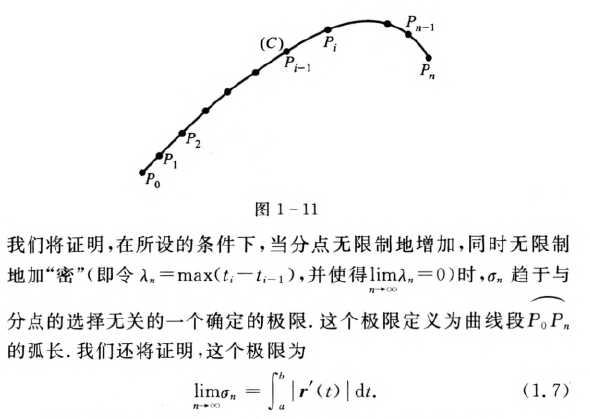
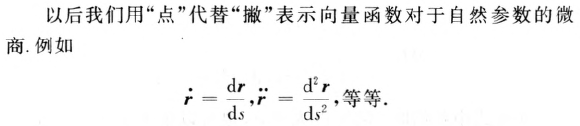
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

案例：

在这里插入图片描述

空间曲线

这一节，我们研究空间曲线的基本理论，主要将研究刻画空间曲线在某点邻近的弯曲程度和离开平面程度的量一曲率和挠率，以及研究空间曲线在一点邻近的近似形状，并找出决定空间曲线的条件.

曲线的密切平面

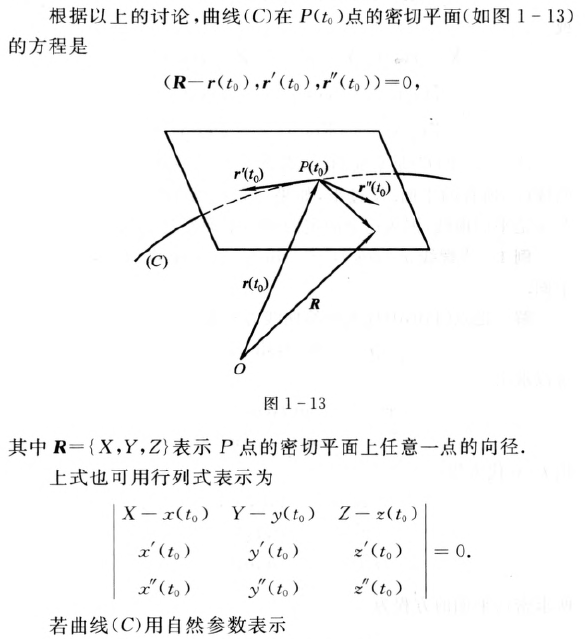
在这里插入图片描述

在这里插入图片描述

案例：

在这里插入图片描述

空间曲线的基本三棱形【重要】

单位切向量

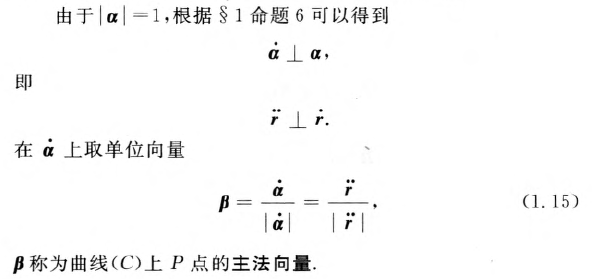
在这里插入图片描述

主法向量

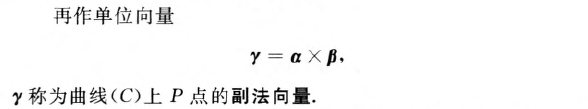
在这里插入图片描述

副法向量

在这里插入图片描述

Frenet标架

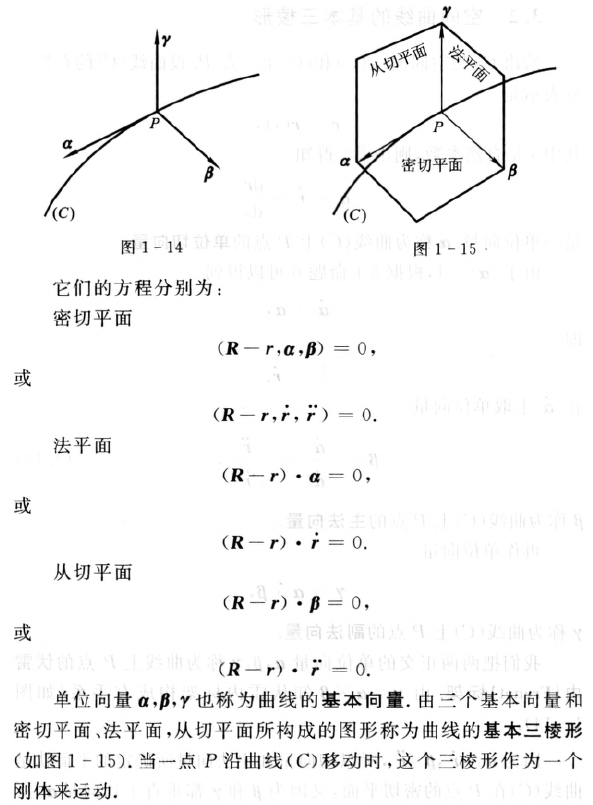
在这里插入图片描述

在这里插入图片描述

计算公式：

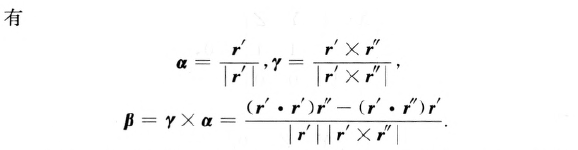
在这里插入图片描述

在这里插入图片描述

螺旋线的案例

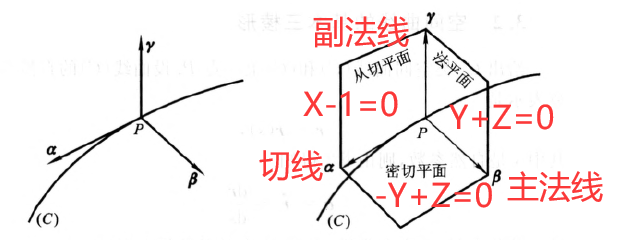
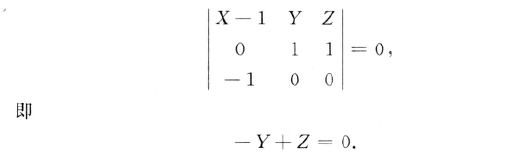
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

接下来主法线，副法线

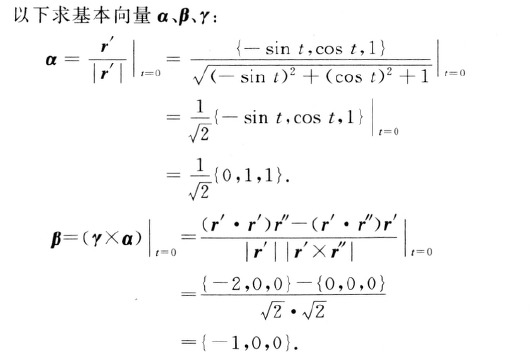
在这里插入图片描述

求基本向量

在这里插入图片描述

在这里插入图片描述

曲线的曲率和曲率半径

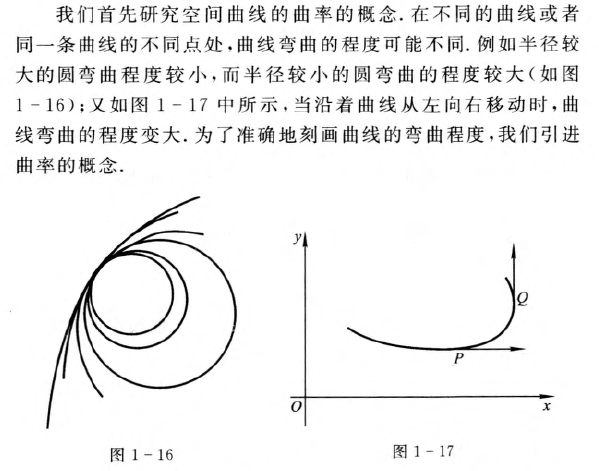
我们首先研究空间曲线的曲率的概念.在不同的曲线或者同一条曲线的不同点处，曲线弯曲的程度可能不同.例如半径较大的圆弯曲程度较小，而半径较小的圆弯曲的程度较大

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

曲率的几何意义

由上述空间曲线的曲率的定义可以看出，它的几何意义是曲线的切向量对于弧长的旋转速度。当曲线在一点的弯曲程度越大，切向量对于弧长的旋转速度就越大，因此曲率刻画了曲线的弯曲程度.

曲率半径：

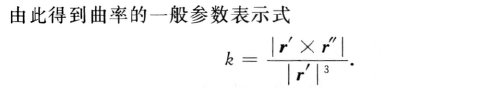
在这里插入图片描述

在这里插入图片描述

曲线的挠率

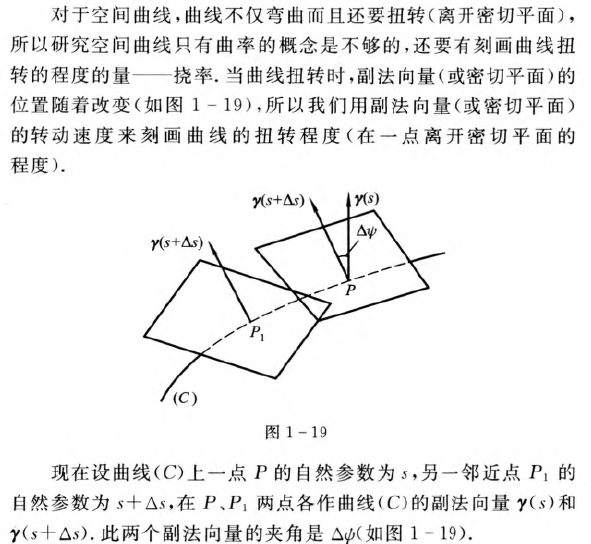
在这里插入图片描述

在这里插入图片描述

挠率的几何意义

此式的几何意义是它的数值为曲线的副法向量（或密切平面）对于弧长的旋转速度。当曲线在一点的扭转程度越大（离开所讨论点的密切平面的程度越大)，副法向量（或密切平面）对于弧长的旋转速度就越大。因此，我们可以用它来刻画曲线的扭转程度

在这里插入图片描述

空间曲线的伏雷内公式

在这里插入图片描述

在这里插入图片描述

案例：

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

案例：

在这里插入图片描述

空间曲线在一点邻近的结构

曲线在某点的曲率和挠率完全决定了曲线在该点邻近的近似形状.

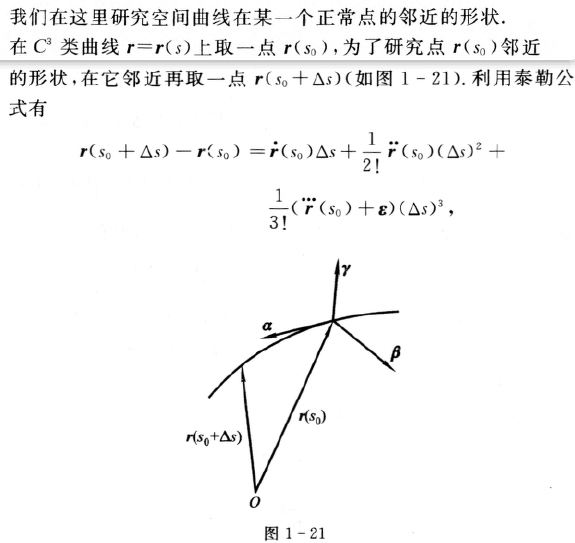
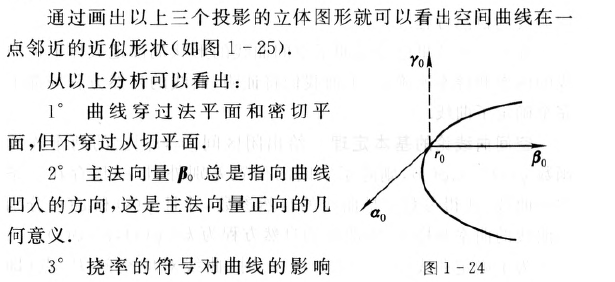
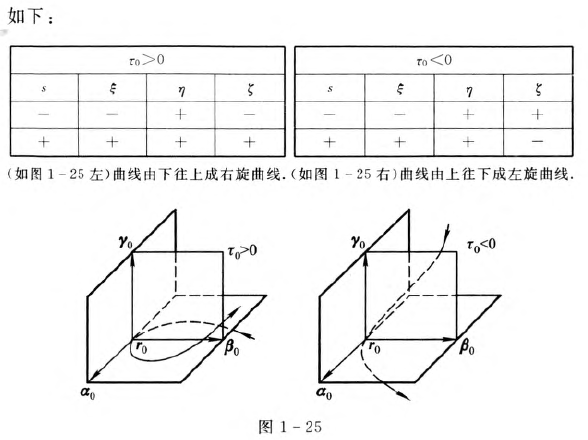
在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

空间曲线论基本定理

在这里插入图片描述

一般螺旋线

在这里插入图片描述

空间曲线论的基本定理指出，曲线的曲率和挠率完全决定了曲线的形状.当曲线的曲率和挠率之间满足多种不同的关系时，就会得到不同类型的曲线.例如，k=0时为直线，t=0时为平面曲线.在这部分我们对常见的曲线一一般螺线进行较为详细的讨论，这对于进一步了解曲线的理论是非常必要的.

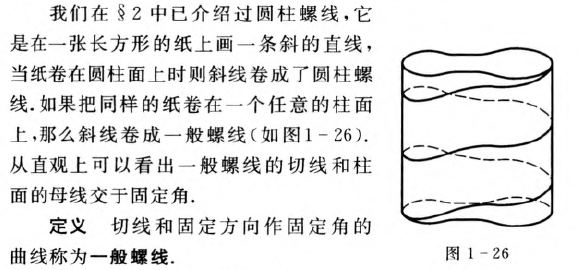
在这里插入图片描述

一般螺旋线的性质：

在这里插入图片描述

在这里插入图片描述

总结

微分几何——梅向明第四版学习笔记（一） & 向量函数和曲线论

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/249282.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

顺序表与链表，栈与队列

顺序表与链表，栈与队列

名词辨析：指针 1.什么是指针，想必大家都不陌生，但是，在这部分的知识中，包含着一类特殊的指针，表面上它只是单个的数字，但它其实代表了作为栈或者队列载体的数组的下标，在实际题目中…
阅读更多...
Golang语言异常机制解析：错误策略与优雅处理

Golang语言异常机制解析：错误策略与优雅处理

前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家。点击跳转到网站https://www.captainbed.cn/kitie。 前言 作为开发者来说，我们没办法保证程序在运行过程中永远不会出现异常，对于异常…
阅读更多...
Java多线程编程中的异常处理策略

Java多线程编程中的异常处理策略

第1章：引言 大家好，我是小黑，咱们今天聊聊异常处理。想必大家在写代码的时候都遇到过各种各样的异常吧？有时候，一个小小的异常如果处理不当，就可能导致整个程序崩溃。特别是在多线程环境下，异常…
阅读更多...
科技云报道：云原生PaaS，如何让金融业数字化开出“繁花”？

科技云报道：云原生PaaS，如何让金融业数字化开出“繁花”？

科技云报道原创。 在中国金融业数字化转型的历史长卷中，过去十年无疑是一部磅礴的史诗。 2017年，南京银行第一次将传统线下金融业务搬到了线上。那一年，它的互联网金融信贷业务实现了过去10年的业务总额。 2021年，富滇银行通过…
阅读更多...
幻兽帕鲁服务器游戏怎么升级版本？

幻兽帕鲁服务器游戏怎么升级版本？

幻兽帕鲁服务器游戏怎么升级版本？自建幻兽帕鲁服务器进入Palworld游戏提示“您正尝试加入的比赛正在运行不兼容的游戏版本，请尝试升级游戏版本”什么原因？这是由于你的客户端和幻兽帕鲁服务器版本不匹配，如何解决？更新…
阅读更多...
配置IPv6静态路由

配置IPv6静态路由

1、静态路由简介 静态路由是一种需要管理员手工配置的特殊路由。 静态路由在不同网络环境中有不同的目的： 当网络结构比较简单时，只需配置静态路由就可以使网络正常工作。 在复杂网络环境中，配置静态路由可以改进网络的性能，并…
阅读更多...
Synchronized作用

Synchronized作用

synchronized能够在同一时刻最多只有一个线程执行该代码 证明如下： public class MyThread {public static void main(String[] args) throws InterruptedException {Ticket ticket new Ticket();Thread aa new Thread(() -> {try {ticket.getCount();} catc…
阅读更多...
性能测试工具架构

性能测试工具架构

背景 性能测试工具（LoadRunner为例） 性能测试工具通常是指那些用来支持压力、负载测试，能够录制和生成脚本、设置和部署场景、产生并发用户和向系统施加持续压力的工具。 性能测试工具录制的是服务端与应用之间的通信数据，而不是…
阅读更多...
怎么进行视频压缩大小？常见的4种压缩方法

怎么进行视频压缩大小？常见的4种压缩方法

在当今数字化的时代，我们经常处理大量的视频文件，无论是用于社交媒体分享、视频制作还是存储在我们的设备中。然而，随着视频质量的提升和分辨率的增加，视频文件的大小也相应地变得更加庞大，给存储、分享和传输带来了一…
阅读更多...
hal库stm32串口接收不定长数据

hal库stm32串口接收不定长数据

参考博客： https://blog.csdn.net/qq_41830158/article/details/121254705 按下面步骤修改实测可用 步骤： 添加串口接收所需变量   打开uart.c文件，在文件顶部的USER CODE BEGIN 0下方添加下列变量 volatile uint8_t rx1_len 0; //接收…
阅读更多...
友思特应用 | 微观指尖世界：OCT成像应用之3D指纹提取与识别

友思特应用 | 微观指尖世界：OCT成像应用之3D指纹提取与识别

欢迎访问官网，探索丰富案例： OCT成像系统 | 光学相干断层扫描 | 谱域OCT | 扫频OCT | 广州友思特科技有限公司 关注“友思特机器视觉与光电”公众号、加入行业交流群或直接联系我们，轻松收获更多技术干货 导读 数字化生活已离不开指纹识别认…
阅读更多...
《区块链简易速速上手小册》第6章：区块链在金融服务领域的应用（2024 最新版）

《区块链简易速速上手小册》第6章：区块链在金融服务领域的应用（2024 最新版）

文章目录 6.1 金融服务中的区块链6.1.1 金融服务中区块链的基础6.1.2 主要案例：跨境支付6.1.3 拓展案例 1：去中心化金融（DeFi）6.1.4 拓展案例 2：代币化资产 6.2 区块链在支付系统中的作用6.2.1 支付系统中区块链的基础…
阅读更多...
小程序定制开发前，应该考虑些什么？

小程序定制开发前，应该考虑些什么？

引言 在移动互联网时代，小程序已经成为许多企业和个人推广业务、提供服务的理想平台。然而，在进行小程序定制开发之前，开发者和业务方需要细致入微地考虑一系列关键因素，以确保最终的小程序既能满足用户需求，又能够顺…
阅读更多...
arcgis 批量删除字段

arcgis 批量删除字段

一、打开ArcToolbox-数据管理工具-字段-删除字段。 二、在输入表中选择要删除字段的要素，在删除字段栏中选择要删除的字段，点击确认即可。
阅读更多...
Java强训day13（选择题编程题）

Java强训day13（选择题编程题）

选择题 编程题 题目1 import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc new Scanner(System.in);String s sc.nextLine();char[] c s.toCharArray();int i 0;int t 0;while (i < c.length) {if (c[i] ! \") {…
阅读更多...
Go语言基础之单元测试

Go语言基础之单元测试

1.go test工具 Go语言中的测试依赖go test命令。编写测试代码和编写普通的Go代码过程是类似的&#xff0c;并不需要学习新的语法、规则或工具。 go test命令是一个按照一定约定和组织的测试代码的驱动程序。在包目录内&#xff0c;所有以_test.go为后缀名的源代码文件都是go …
阅读更多...
Maven的Docker镜像二次打包，再次推送至Harbor中

Maven的Docker镜像二次打包，再次推送至Harbor中

之所以如此操作&#xff0c;主要原因是&#xff0c;官版的镜像中默认的setting.xml已内置好&#xff0c;不容易修改&#xff0c; 重新二次打包&#xff0c;可以指定我们自己的setting.xml配置&#xff0c;配置自己的私服地址以及解决默认Maven仓库国内下载速度慢的问题 一、创…
阅读更多...
ssl数字证书是什么

ssl数字证书是什么

SSL证书是一种数字证书&#xff0c;用于在网络传输中提供加密和身份验证功能&#xff0c;从而保护数据的安全性和完整性。正规的SSL证书大多是由由权威的证书颁发机构&#xff08;CA&#xff09;颁发的&#xff0c;例如Certum、Digicert、Sectigo等&#xff0c;它们颁发的SSL数…
阅读更多...
[机器学习]简单线性回归——最小二乘法

[机器学习]简单线性回归——最小二乘法

一.线性回归及最小二乘法概念 2.代码实现 # 0.引入依赖 import numpy as np import matplotlib.pyplot as plt# 1.导入数据 points np.genfromtxt(data.csv, delimiter,) # points[0,0]# 提取points中的两列数据&#xff0c;分别作为x&#xff0c;y x points[:, 0] y poi…
阅读更多...
【Linux】初始进程地址空间

【Linux】初始进程地址空间

最近&#xff0c;我发现了一个超级强大的人工智能学习网站。它以通俗易懂的方式呈现复杂的概念&#xff0c;而且内容风趣幽默。我觉得它对大家可能会有所帮助&#xff0c;所以我在此分享。点击这里跳转到网站。 目录 一、再谈fork二、程序地址空间2.1代码验证 三、虚拟地址&am…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023