深度学习之反向传播

反向传播英文叫做Back Propagation。

为什么需要使用反向传播

对于简单的模型我们可以用解析式求出它的损失函数的梯度，例如，其损失函数的梯度就是，我们可以通过我们的数学知识很容易就得到其损失函数的梯度，继而进行使用梯度下降算法是参数（权重）更新。

但是这仅限于对于简单的模型，一旦模型的深度增加，模型变得复杂，我们就很难直观的看出损失函数的梯度。

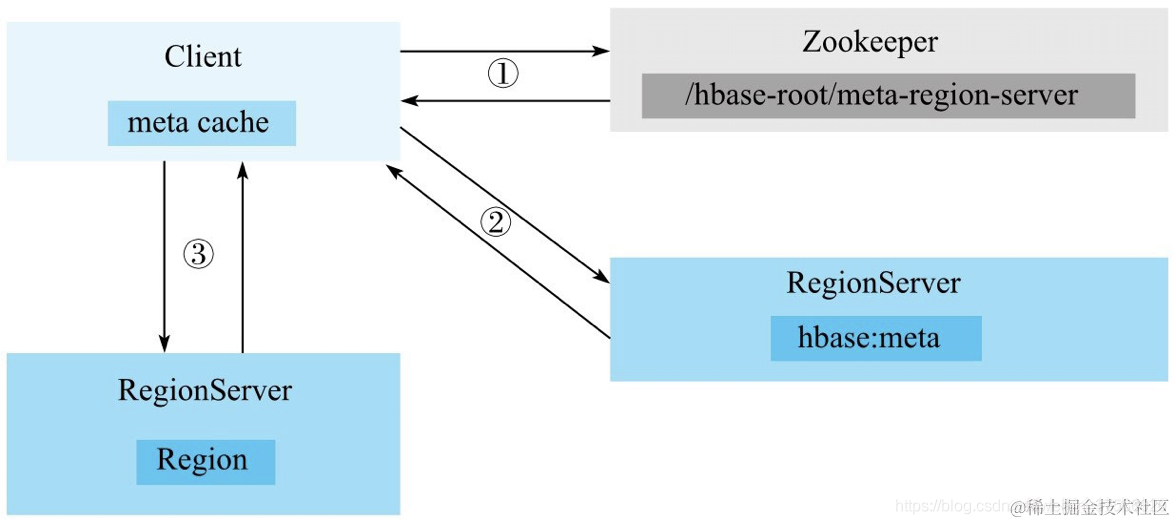
例如这个模型，每连接的两个节点里面都有相应的权重，权重数量相当的多。

在这个图中，最左边五个输入表示的是输入的x1到x5，连线表示经过和权重的混合运算，，第二层是隐藏层，输入的样本数量是5，输出的样本数量是6，那么输出相当于是输入6*5的权重矩阵*5*1的样本矩阵得到的结果。显然，我们有三十个不同的权重，同理，第二层到第三层之间有42个权重，第三层到第四层之间有49个权重，依次类推，显然权重的数量不便于我们直接写出损失函数的梯度。

如何进行反向传播：

前馈：

面对这样的复杂网络的时候我们要回过来想一下，能不能把我们的网络看做是一个图，图中可以来传播我们的梯度，最终我们根据链式法则，把梯度都求出来。这种算法我们称之为反向传播算法，

我们以两层的神经网络为例：

不妨设X是输入的矩阵是 $\mathbb{R}^{^{n}}$ ，输入的维度是n，（对于向量来说，维度即是长度）。设为输出的维度是m，第一层的输出是W1X，有的时候W会加转置，对于不加转置的W1来说，W1是m*n的矩阵，对于加了转置的W1来说，转置之后 $W^{^{T}}$ 是m*n，那么转置之前的W是n*m阶矩阵。注意我们的输出还要加上一个b1（Bias偏移量），显然，矩阵相乘（MM=Matrix multiplication）之后得到的是一个m维的向量，此时加上去的b1也要是一个m维的向量。

我们将W1*X+b1的运算用图示表示出来，这称作一个层，也就是我们的第一层。然后我们再对得到的输出进行又一轮新的运算。

不妨设第一层得到的输出是A，则W2*A+b2就是第二层，在图示中已经表现出来，绿色的部分表示我们进行的运算，蓝色的部分也就是我们的权重和偏移量，肉色的部分是我的每一步得到的输出。

在计算图中，对于不同的计算模块（绿色部分），它求局部的偏导的方法是不同的。例如矩阵的求导可以参考《matrix cookbook》中的公式。

不过这一部分我们并不要求会对矩阵求导，计算机会给你答案。

但是，其实我们那个两层的神经网络其实可以展开为一层。

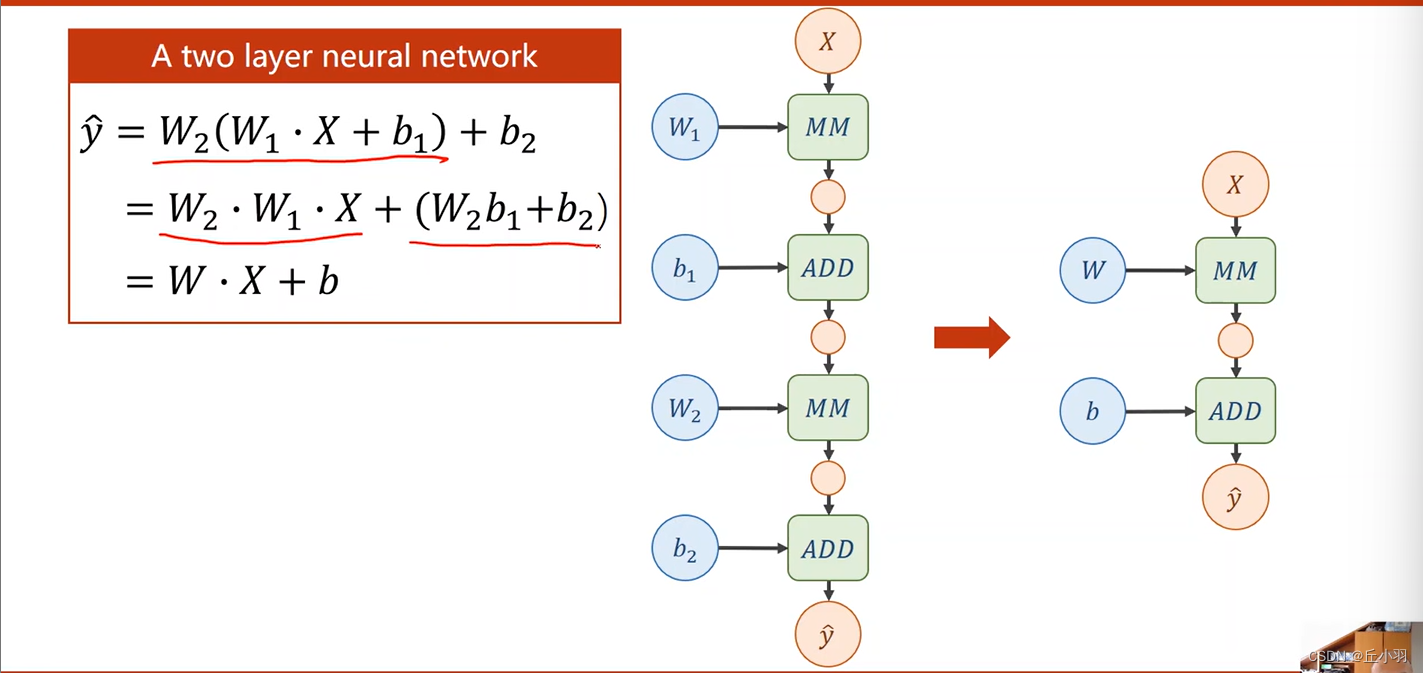
如果只进行线性变换，最终不管我们有多少层，最终都会统一成图中右边部分的形式。也就是层数多喝层数少时没区别的，

这时候我们选择了那么多权重是不是就没意义了呢？我们可以选择少量的权重，但是我们选择你们多不是浪费时间吗？其实不然，我们可以对每一层的结果进行处理，使每个权重包含的信息更多，这样就不能省去了。

例如，我们可以对第一层的结果进行非线性变化（加一个非线性的变化函数），我们对输出向量里面的每一个值，都应用一个非线性函数，比如说sigmoid函数我们将每一个成员都带入sigmoid函数，。这样的话，我们就没办法再做这种展开了，我们就保留了更多的权重，保留更多的信息。

反向传播：

接下来我们来说求导。

对于复合函数求导，这里就不再多说。

接下来我我们看back propagation（反向传播）的过程。

首先第一步，我们需要创建计算图。例如：

在计算过程中，我们首先要做的是前馈，我们首先沿着图里的箭头，也就是边的方向，由输入向最终的loss传播，计算最终的loss。在计算的过程中，我们在拿到了x和权重，我们要计算我们的输出z，以及它对于x和权重w的导数，f做的运算是得到梯度函数的值，即既得到和，又得到输出的结果z。

前馈的过程是从输入，一直往前算，往loss算。我们往前计算的时候保留了梯度函数，当我们得到loss的时候，带入loss对于z的梯度函数，得到，拿到偏导之后，我们在经过f的时候，我们已知loss对z的偏导，以及和，这个时候我们就可以计算出来loss对x的导数，和loss对w的导数。这里我们有个问题，我们要将损失降到最小，得到loss对w的损失函数不就行了吗，因为我们需要更新的是w啊，那我们为什么要求出loss对x的梯度呢？

在图中，我们的x并不是表示我们的初始输入，我们表示的是某一层的输入，该层可能是隐藏层，那么这时x是原始样本输入经好多权重的运算得到的结果，只有求出loss对x的梯度，才能前馈得到loss对前面权重的梯度。

我们将得到的梯度不断往前相乘就得到loss对该层损失的梯度。

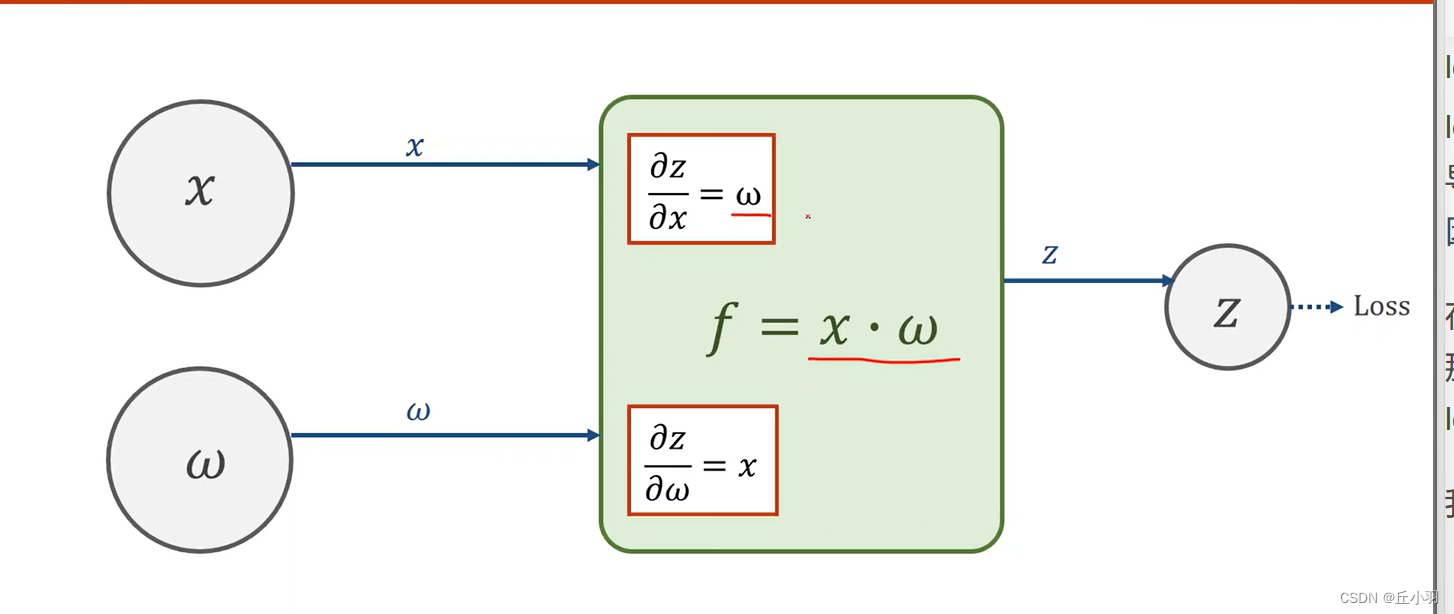
总的来说，就是某一层的输入和权重，接入到一个函数计算模块里面，也就是f，f可以计算局部的梯度，然后我们只要能拿到损失对最后一层输出y的梯度，然后不断往前传播。

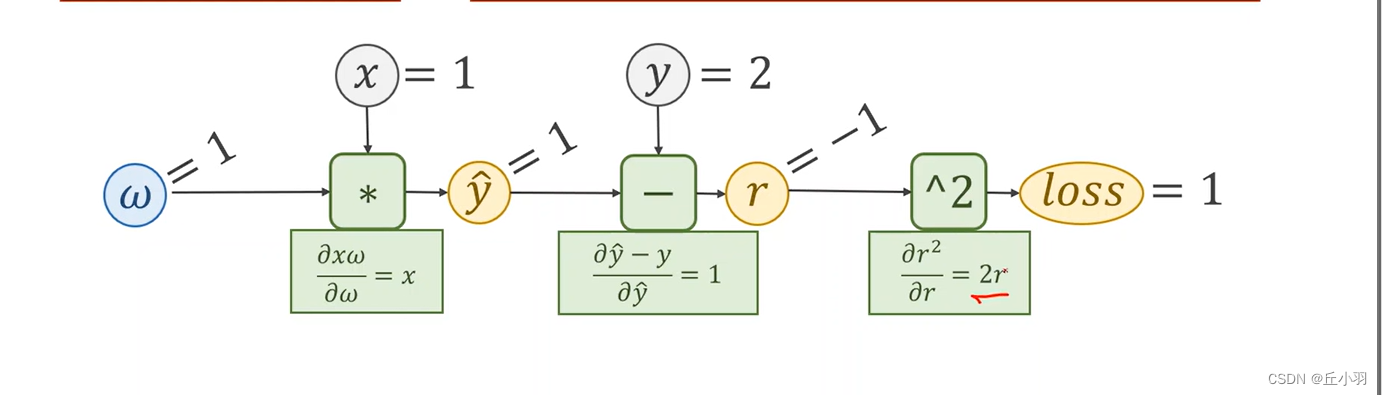
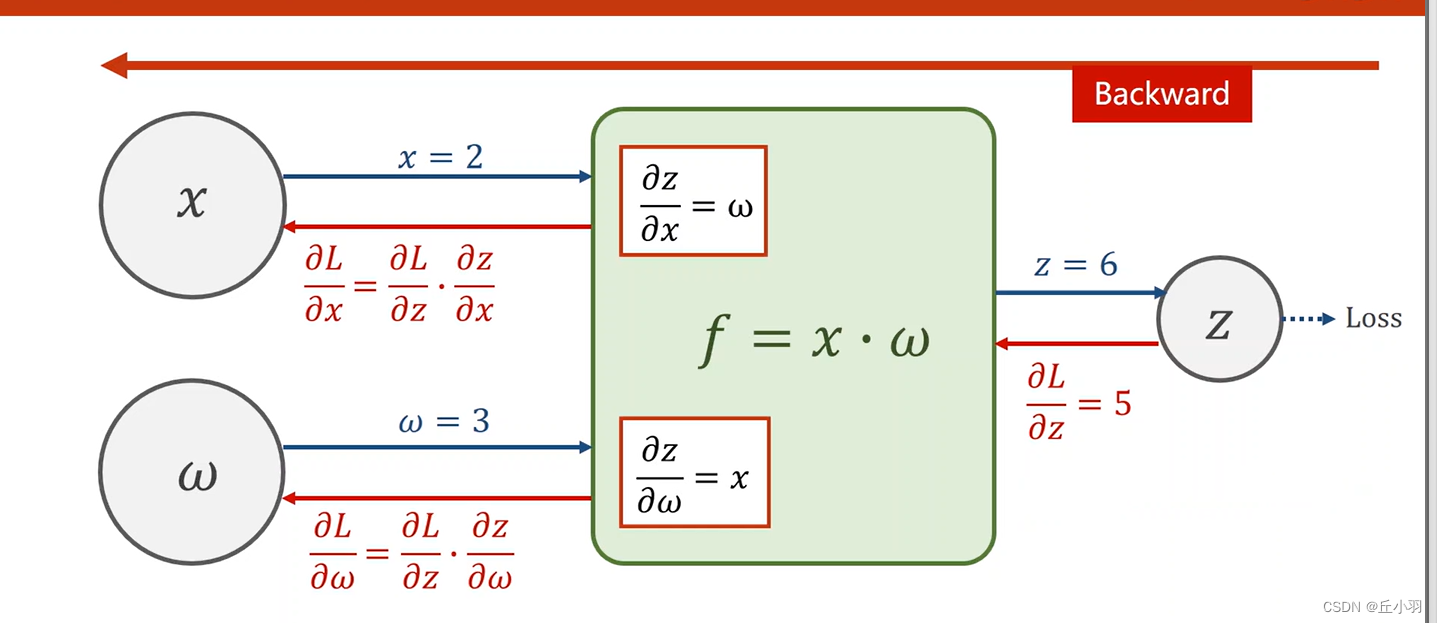
如图，我们在前馈过程中，我们能算出我们的每个输出结果对输入结果的梯度（每个黄色项对前一个黄色项的梯度（第一层是对w的梯度））。注意，只要中间结果在前馈的过程中使用到了需要求的权重，那么loss对于这个值的梯度是做要求的。

下图是我们反向传播的过程：

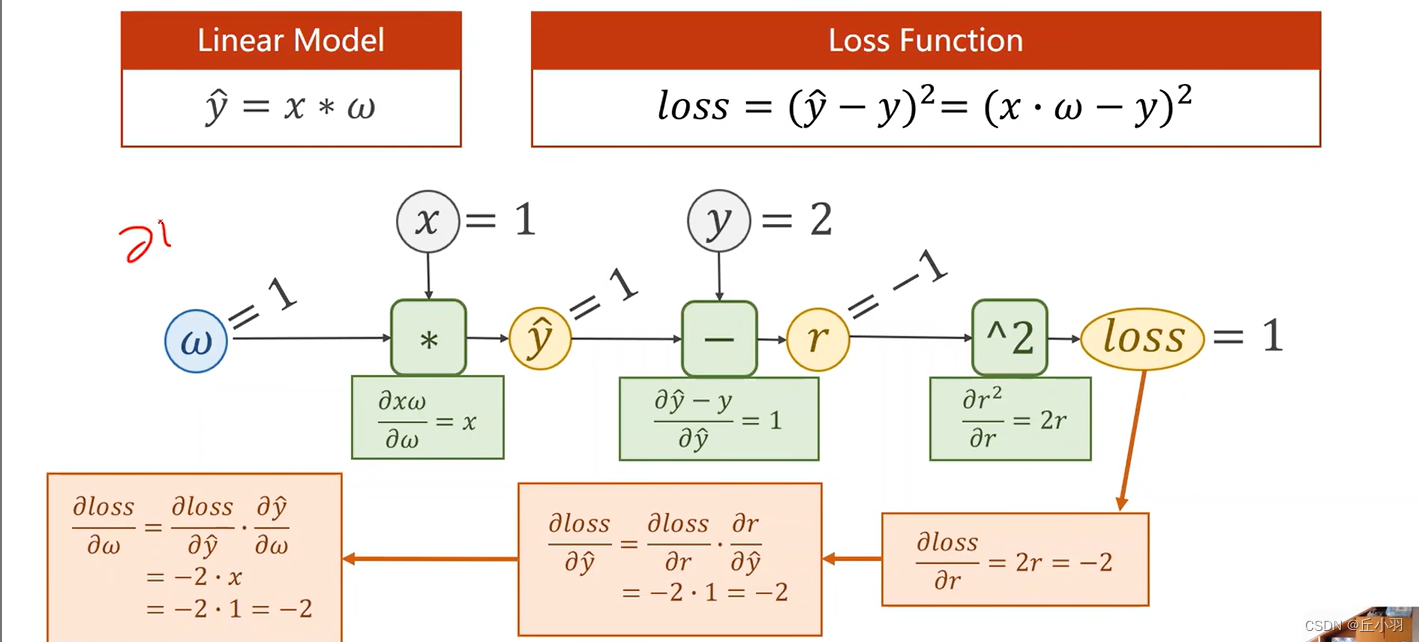
即先前馈，再反向。

前馈过程计算每一层的输出值，并计算梯度函数，反向的过程中，利用链式法则，求出loss对每一层的权重的梯度，不断往前走，直到求出来对我们所需要更新的权重的梯度。

这时看似我们在求损失对权重梯度的时候我们没有用到损失值（显然，我们反向传播的第一项是求损失对残差r的梯度，而梯度函数是2r，我们并没有使用到loss），这时我们有必要保留loss吗？答案是有必要，loss对于我们评估模型的好坏很重要，损失越小，说明模型的预测效果越好，也就是越接近真实结果，我们可以通过对损失进行可视化来评价模型。