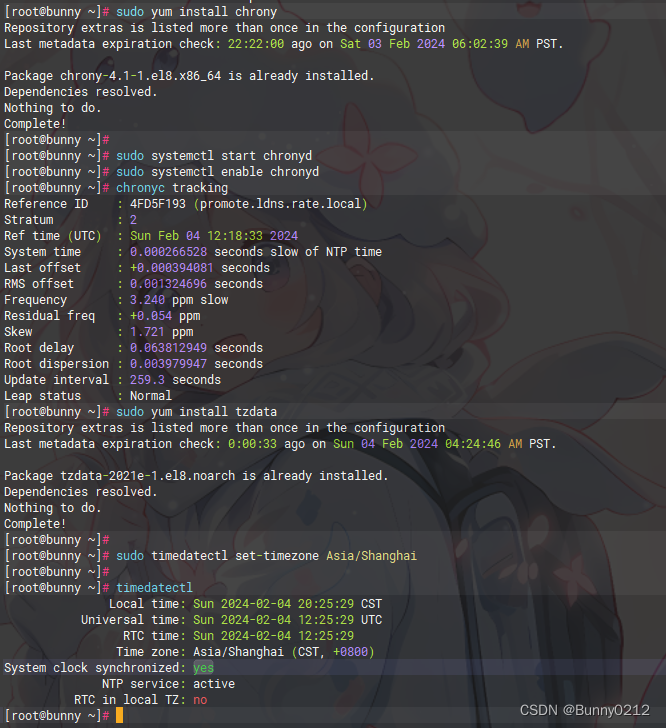
Linux校准时间 Centos
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.rhkb.cn/news/251752.html
如若内容造成侵权/违法违规/事实不符,请联系长河编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
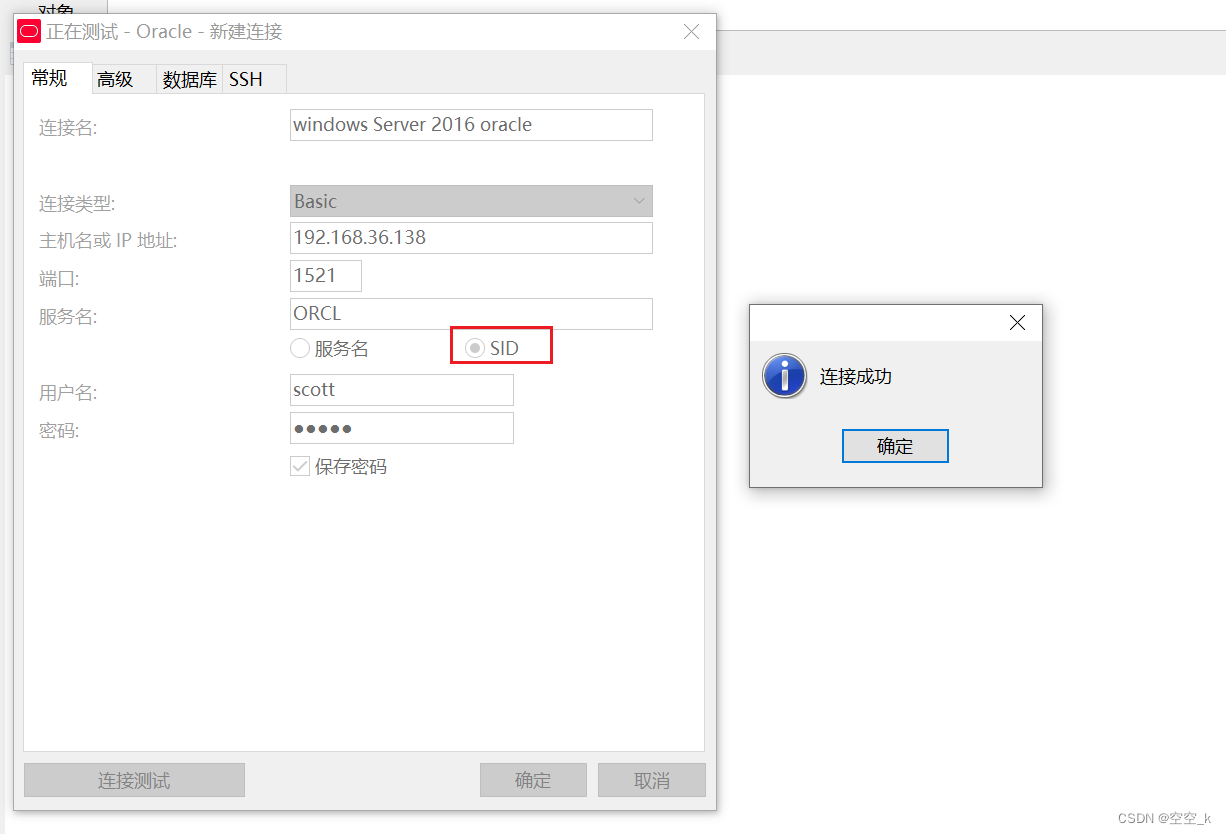
安装配置Oracle 11g 、PLSQL及使用Navicat远程连接Oracle
目录
一、下载
二、安装
1.执行安装程序
2.配置安全更新
3.安装选项
4.系统类
5.网络安装选项
6.选择安装类型
7.选择产品语言
8.选择数据库版本
9.指定安装位置
10.选择配置类型
编辑11.指定数据库标识符
12.指定配置选项
13.电子邮箱
14.指定数据库存储…
Nucleosome, Recombinant Human, H2BK120ub1 dNuc, Biotinylated
EpiCypher(国内授权代理商欣博盛生物)是一家为表观遗传学和染色质生物学研究提供高质量试剂和工具的专业制造商。EpiCypher生产的在E. coli中表达的重组人单核小体(组蛋白H2A、H2B、H3和H4各2个;accession numbers:H2A-P04908;H2B-O60814;H3.1-P68431;H4…
重写Sylar基于协程的服务器(3、协程模块的设计)
重写Sylar基于协程的服务器(3、协程模块的设计)
重写Sylar基于协程的服务器系列: 重写Sylar基于协程的服务器(0、搭建开发环境以及项目框架 || 下载编译简化版Sylar) 重写Sylar基于协程的服务器(1、日志模…
IP风险画像在企业网络安全中应用
随着企业数字化的不断深入,网络安全问题日益突显。IP风险画像作为一种综合性的网络安全工具,为企业提供了更全面的风险评估和防范手段。本文将结合一个实际案例,深入探讨IP风险画像在企业网络安全中的成功应用。
案例背景
一家大型金融机构…
苹果电脑录制视频在哪里?教你快速找到它!
录制电脑屏幕已成为了许多用户日常所需的操作,无论是录制在线课程、游戏过程,还是网络会议,一款好的录屏软件能帮助用户高效、便捷地完成任务。苹果电脑是当今主流的计算机设备之一,可是很多用户不知道苹果电脑录制视频在哪里。在…
LeetCode:283. 移动零
283. 移动零 1)题目2)代码方法一:两层for循环方法二:使用双指针 3)结果方法一结果方法二结果 1)题目
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的…
用GOGS搭建GIT服务器
GOGS官网
Gogs: A painless self-hosted Git service 进入文件所在目录
cd /usr/local/develop
解压文件 tar -xvf gogs_0.13.0_linux_amd64.tar.gz 解压之后 进入gogs 目录
cd gogs 创建几个目录 userdata 存放用户数据 log文件存放进程日志 repositories 仓库根目…
【python】OpenCV—Tracking(10.1)
学习来自《Learning OpenCV 3 Computer Vision with Python》Second Edition by Joe Minichino and Joseph Howse 文章目录 检测移动的目标涉及到的 opencv 库cv2.GaussianBlurcv2.absdiffcv2.thresholdcv2.dilatecv2.getStructuringElementcv2.findContourscv2.contourAreacv2…
React16源码: React中处理hydrate的核心流程源码实现
hydrate 1 )概述
hydrate 在react当中不算特别重要, 但是很多时候会用到的一个API这个 API 它主要作用就是在进入第一次渲染的时候,如果本身 dom 树上面已经有一个dom结构存在是否可以去利用这一部分已经存在的dom,然后去避免掉在第一次渲染…
小华和小为的聚餐地点 - 华为OD统一考试
OD统一考试(C卷) 分值: 200分 题解: Java / Python / C++ 题目描述
小华和小为是很要好的朋友,他们约定周末一起吃饭。
通过手机交流,他们在地图上选择了多个聚餐地点(由于自然地形等原因,部分聚餐地点不可达)。
求小华和小为都能到达的聚餐地点有多少个?
输入描述…
在本地运行大型语言模型 (LLM) 的六种方法(2024 年 1 月)
一、说明 (开放)本地大型语言模型(LLM),特别是在 Meta 发布LLaMA和后Llama 2,变得越来越好,并且被越来越广泛地采用。 在本文中,我想演示在本地(即在您的计算机上&#x…
最值得推荐收藏的 7 款 Android 系统修复软件,快速的修复手机异常
在当今世界,移动设备是我们生活的重要组成部分。我们将它们用于沟通、工作、娱乐和许多其他目的。然而,随着不断的使用,它们通常会面临速度慢、崩溃等问题。这可能会让人烦恼和沮丧。但是,值得庆幸的是,您可以在 Andro…
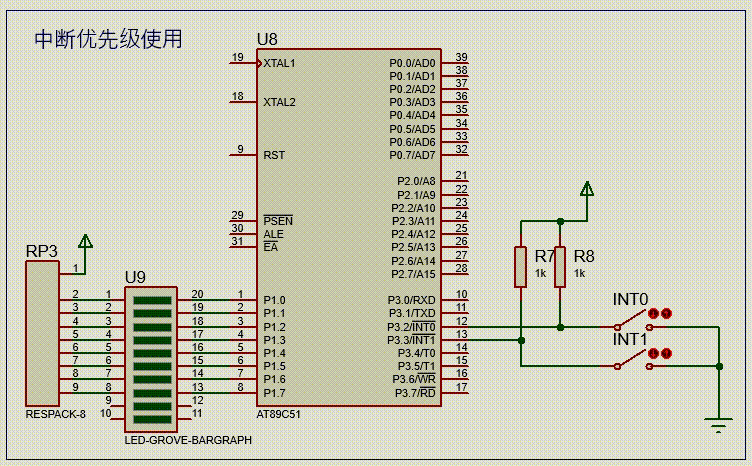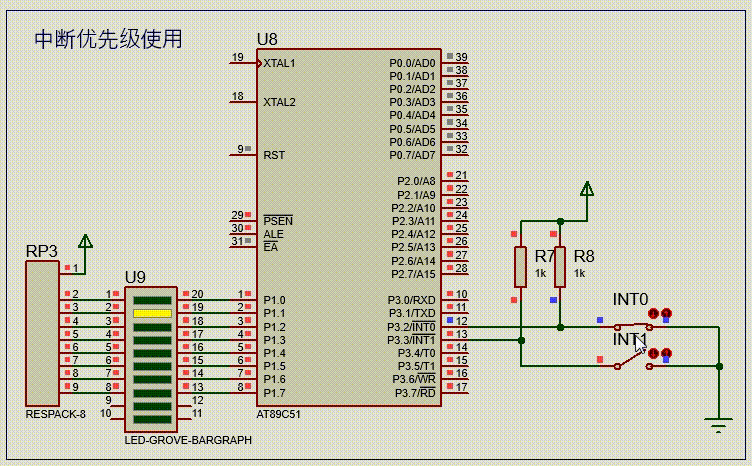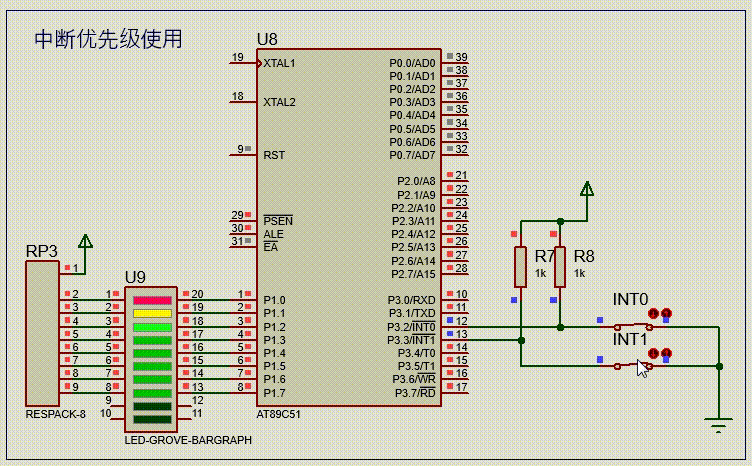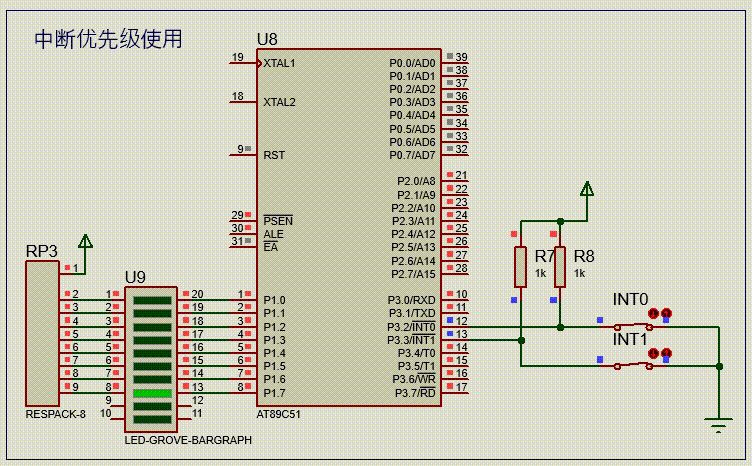
【51单片机系列】中断优先级介绍及使用
文章来源:《51单片机原理及应用(第3版)》5.4节。 51单片机采用了自然优先级和人工设置高、低优先级的策略。
当CPU处理低优先级中断,又发生更高级中断时,此时中断处理过程如下图所示。
一个正在执行的低优先级中断服…
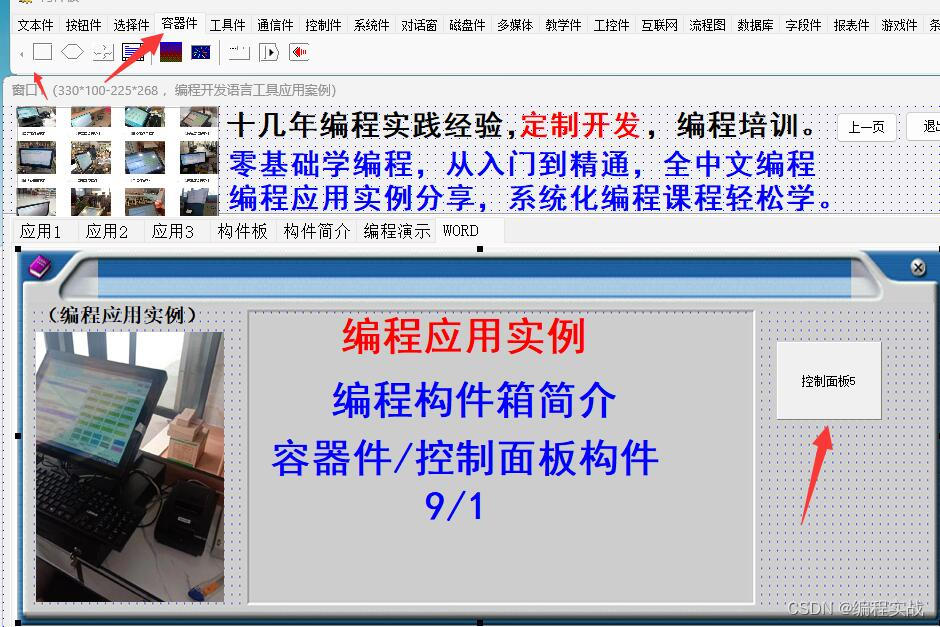
零基础学编程系列,从入门到精通,中文编程开发语言工具下载,编程构件容器件之控制面板构件用法
零基础学编程系列,从入门到精通,中文编程开发语言工具下载,编程构件容器件之控制面板构件用法
一、前言
编程入门视频教程链接
https://edu.csdn.net/course/detail/39036
编程工具及实例源码文件下载可以点击最下方官网卡片——软件下载…
【安装指南】nodejs下载、安装与配置详细教程
目录
🌼一、概述
🍀二、下载node.js
🌷三、安装node.js
🍁四、配置node.js 🌼一、概述 Node.js 是一个基于 Chrome V8 引擎的 JavaScript 运行时,用于构建可扩展的网络应用程序。Node.js 使用事件驱动、…
机器学习笔记-聚类算法
机器学习笔记-聚类算法 聚类算法K-meansk-means的模型评估k-means的优化 PCA降维主成分分析-PCA降维 PCAK-means例子 聚类算法K-means 代码
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_blobs
from sklearn.cluster import KMeans
…
JS第一天、数据类型检测、内存释放
复习:
以下类型都是 object
console.log(typeof new Object); console.log(typeof new Array()); console.log(typeof new Date()); console.log(typeof new RegExp()); console.log(typeof new String()); console.log(typeof new Number()); console.log(typeof…
乐意购项目前端开发 #7
一、购物车 本地购物车
创建cartStore.js文件
创建cartStore.js文件, 将购物车列表数据存在pinia中 import { ref, computed } from "vue";
import { defineStore } from "pinia";
import { useUserStore } from "./user";
import {insertCart…
C#,哥伦布数(Golomb Number)的算法与源代码
1 哥伦布数(Golomb Number)
哥伦布数(Golomb Number)是一个自然数的非减量序列,使得n在序列中正好出现G(n)次。前几个15的G(n)值为:1 2 2 3 3 4 4 4 5 5 5 6…
最新文章
- wordpress epub插件/长沙seo代理商
- abc建站的网站/推广产品的软文怎么写
- 网站建设的教学视频/如何推广网页
- 空间制作网站/网络营销推广策划步骤
- 学完html怎么做网站/百度惠生活商家怎么入驻
- 大气集团网站源码/网站关键词优化排名外包
- Nuc9 Truenas 和 Macmini4组雷电网桥 上传速度异常 1Mbp/s 解决
- OpenTK 中帧缓存的深度解析与应用实践
- Java重要面试名词整理(一):性能调优
- Docker容器命令
- Python从0到100(七十八):神经网络--从0开始搭建全连接网络和CNN网络
- Qt:QMetaObject::connectSlotsByName实现信号槽自动关联
推荐文章