🎇个人主页：Ice_Sugar_7
🎇所属专栏：初阶数据结构
🎇欢迎点赞收藏加关注哦！

🍉快速排序

快排的基本思想是从序列中选某一个元素为key，然后开始多次排序，每次排完后key左边的值都小于key，右边则都大于key。然后对key左右的区间（[begin,key - 1]和[key+1,end]，左右都是闭区间）分别进行递归，划分为更小的区间，直到成为有序区间再返回。最终整个区间就是有序的

所以，快排的递归过程可以看作是一棵二叉树

●每次选择一个基准元素，将小于基准的元素放在左子树，大于基准的元素放在右子树。然后对左子树和右子树分别进行快排。这个过程可以一直递归下去
●直到每个子树只剩下一个或没有元素（即递归到叶子节点）时返回

快排的框架如下：

void QuickSort(int* a, int left, int right) {  //left和right是区间端点（都是闭区间）if (right <= left)  //right如果小于left，那么这个区间不存在；right==left说明这个区间只有一个元素return;int key = PartSort(a, left, right);  //PartSort是找key的函数，下面会讲QuickSort(a, left, key - 1);QuickSort(a, key + 1, right);
}

快排的核心就是找key，有三种方法找key，下面依次介绍

先解释两个概念：找大和找小：

找大：一直向左走或向右走，直到找出比key大的值，或者找不到
找小：一直向左走或向右走，直到找出比key小的值，或者找不到

🍌霍尔版本

霍尔版本的快排是原始版本，先看动图：

这种方法具体步骤如下：
●假设序列最左边的值为key，让右边（right）先走，找小。
●找到后停下，轮到左边（left）走，找大。找到后停下，交换此时left和right处的元素。
●重复这个过程，直到left和right相遇，交换此时left和key处的值
●到这里，序列以key为分界线，划分左、右两个区间

注意：假设哪边为key，那么一开始就要让另一边先走

int PartSort1(int* a, int left, int right) {int keyi = left;while (left < right){//右边先走，找小while (left < right && a[right] >= a[keyi]){--right;}//左边找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);return left;
}

🍌挖坑法

相较于霍尔版，挖坑法的逻辑更好理解

●假设序列最左边的值为key，右边先走，直到遇见比key小的值，就把这个值填入坑中，然后自己成为新的坑
●right走完后，轮到left走，left是遇到比key大的值才停下来。然后同样把这个值扔进坑里，自己成为新的坑
●left和right相遇时，将key填入坑中（此时坑位就是left和right所在位置）

int PartSort2(int* a, int left, int right) {int hole = left;int tmp = a[hole]; //保存最开始坑位的值while (left < right){while (left < right && a[right] > tmp)  //相等的话可以不移动，不会死循环{--right;}a[hole] = a[right];  //遇到比坑位小的值hole = right;  //更新坑位下标while (left < right && a[left] < tmp){--left;}a[hole] = a[left];hole = left;  //更新坑位}a[hole] = tmp;return hole;
}

🍌前后指针法

●定义两个指针prev、cur，prev一开始位于最左边，cur在prev的下一个位置。让cur开始走，往右找小，如果遇到比key小的值，那就让prev++，然后交换a[prev]和a[cur]
（但如果prev++之后和cur一样的话，那就没必要交换了）

●当cur遇到比key大的值时，此时prev不走，cur照常走
按照这种规律，那prev就会在第一个比key大的值的前面停下来
而cur继续走，再遇到比key小的值时，由于prev++，所以就会将那个小的数和这个大的数交换位置，相当于把大的数和小的数分别甩到后面和前面

●当cur走到最右边时，循环结束，交换prev和key处的值
（此时cur处的值比a[key]小，就把它甩到前面了）

int PartSort3(int* a, int left, int right) {int mid = GetMidi(a, left, right); //采用三数取中的方法取中间数，优化快排，下面会讲这种方法Swap(&a[left], &a[mid]);int key = mid;int prev = left, cur = left + 1;while (cur <= right){if (a[cur] < a[key] && ++prev != cur)  //遇到比key小的值，就++prev，然后若prev和cur不相等，那就交换prev和cur{Swap(&a[prev], &a[cur]);}//如果比key大，那cur就继续走++cur;}Swap(&a[prev], &a[key]);return prev;
}

---

🍉快排优化

由于快排的递归过程可以看作是二叉树，所以我们可以根据二叉树的特点对快排进行优化，提高其效率

🍌三数取中

对于同样的n个元素，如果二叉树越斜，那么它就越深；而如果二叉树比较平衡，那么深度就比较浅（完全二叉树深度最浅）
前面我们快排取的key要么是最左，要么是最右，如果key处的值刚好是最大值或最小值的话，那对快排是相当不利的
而反之，如果key是序列的中位数，或者是接近中位数（总之就是尽可能不让它成为最值），那就可以极大提高快排的效率
所以写一个三数取中的函数，从left、right和mid（序列中间的那个数）三者中取大小在中间的数，然后把它和left处的值交换，让它成为key

int GetMidi(int* a, int left, int right) {int mid = (left + right) / 2;if (a[left] > a[right])  //左>右{if (a[mid] > a[left])return left;if (a[right] > a[mid])return right;elsereturn mid;}else  //右>左 {if (a[left] > a[mid])return left;if (a[mid] > a[right])return right;elsereturn mid;}
}

---

🍌小区间直接插入

对于完全二叉树而言，越往下结点数越多，递归的成本也越来越大
拿常规的快排来说（递归过程比较接近完全二叉树），递归到比较深层次时（此时区间长度相对而言比较小）我们不用快排，转而使用直接插入排序，可以降低时间成本
优化后代码如下：

void QuickSort1(int* a, int left, int right) {if (right <= left)return;if (right - left + 1 <= 10)  //区间长度小于等于10时就采用直接插入排序InsertSort(a, right - left + 1); else{int key = PartSort1(a, left, right);QuickSort1(a, left, key - 1);QuickSort1(a, key + 1, right);}
}

---

🍌非递归快排

当递归层数过深时，就会有栈溢出的风险，此时要使用非递归快排，这种思路通过栈来实现

思路：
●把区间端点下标（左右都是闭区间）入栈，然后出栈，取到端点下标，找key
●由key可以将原区间划分为左、右两个子区间，将这两个区间的端点入栈，然后继续找key，划分区间
●重复上面的步骤，当栈为空时，排序完成

void QuickSortNonR(int* a, int left, int right) {Stack st;StackInit(&st);StackPush(&st, left);  //左端点入栈StackPush(&st, right);while (!StackEmpty(&st)){int key = PartSort1(a, left, right);right = StackTop(&st);  //取栈顶元素StackPop(&st);  //出栈left = StackTop(&st);StackPop(&st);if (left < key - 1)  //区间至少有两个元素才入栈{StackPush(&st, left);StackPush(&st, key - 1);}if (right > key + 1)  //区间至少有两个元素才入栈{StackPush(&st, key + 1);StackPush(&st, right);}}
}

你会发现，虽然叫非递归，但是整个过程几乎和递归一模一样

---

🍉归并排序

🍌递归

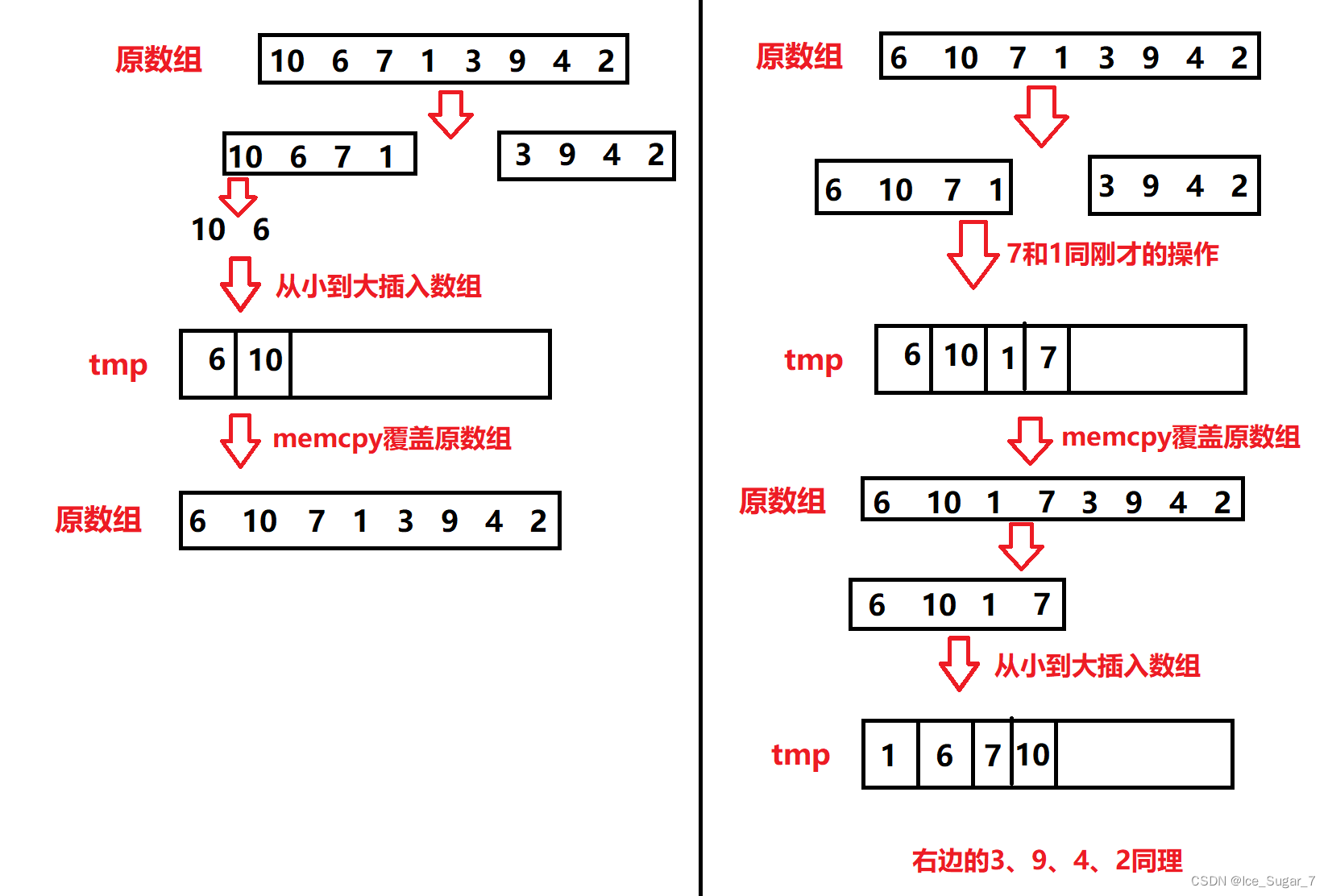
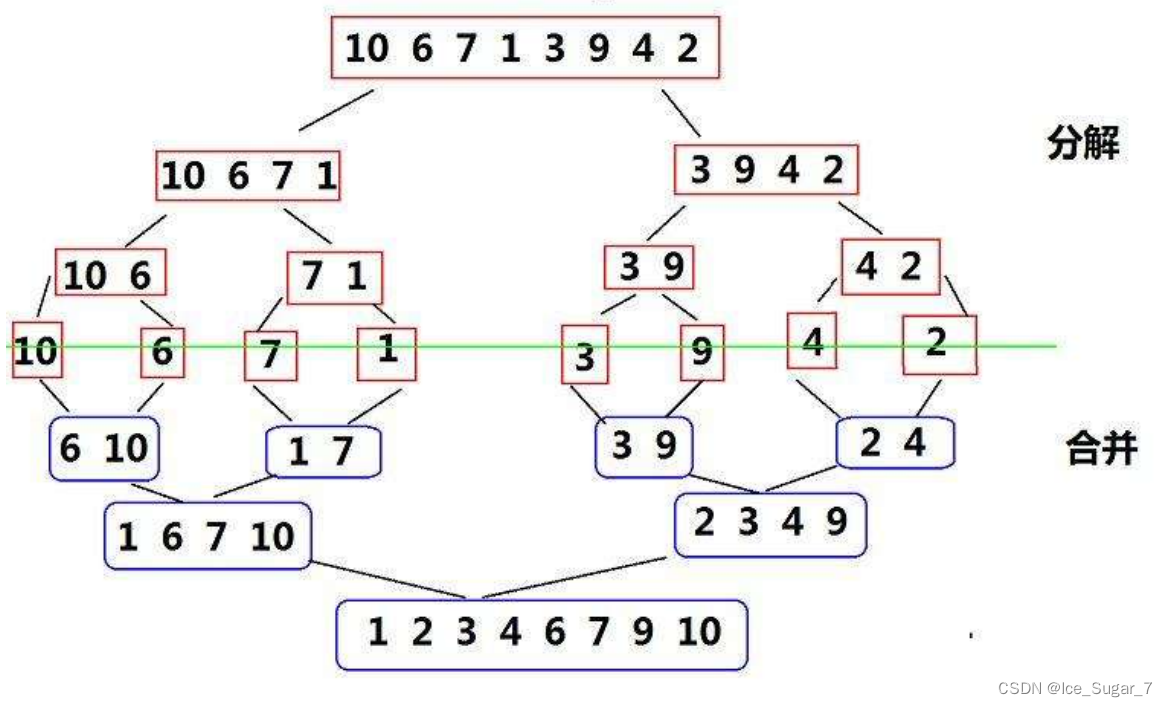
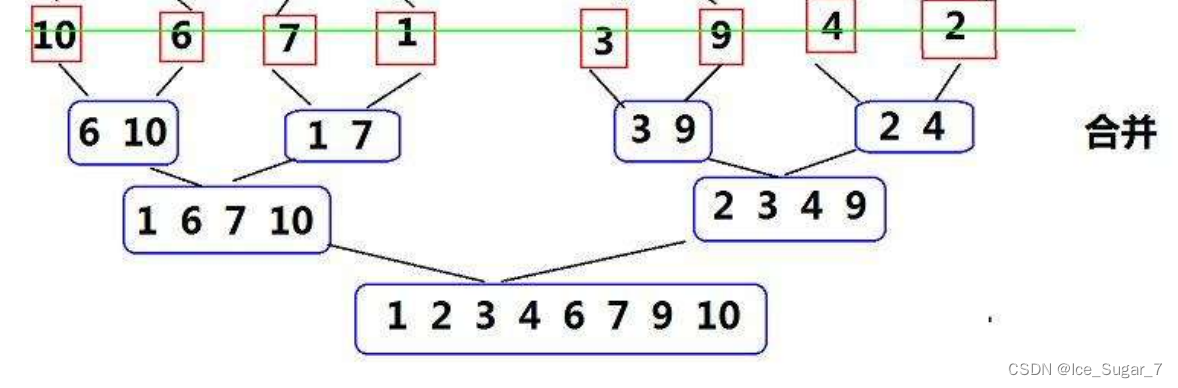
和快排差不多，也是先分割区间，不过归并排序不用找key，而是直接从中间分割
分割到有序时，将元素从小到大尾插到临时数组tmp。插好后将tmp拷贝到原数组
示意图如下：

void _MergeSort(int* a,int* tmp, int left,int right) {if (left >= right)return;int mid = (left + right) / 2;int left1 = left, right1 = mid;  //左区间的左端点、右端点int left2 = mid + 1, right2 = right; //右区间的左端点、右端点_MergeSort(a, tmp, left1, right1);  //左区间进行排序_MergeSort(a, tmp, left2, right2);  //右区间进行排序int i = left;  //控制tmp的下标//合并有序数组（归并中的“并”）while (left1 <= right1 && left2 <= right2){if (a[left1] < a[left2])tmp[i++] = a[left1++];elsetmp[i++] = a[left2++];}//确保剩下的元素都进tmpwhile (left1 <= right1){tmp[i++] = a[left1++];}while (left2 <= right2){tmp[i++] = a[left2++];}memcpy(a + left, tmp + left, sizeof(int) * (right - left + 1));
}void MergeSort(int* a,int n) {int left = 0;int right = n - 1;int mid = (left + right) / 2;int* tmp = (int*)malloc(sizeof(int) * n);_MergeSort(a, tmp,left,right);free(tmp);
}

🍌非递归

将序列中的元素先合并为两个（1,1合并），然后两个两个合并为四个（2,2合并），再合并为八个……
使用非递归的话需要注意边界，因为每次是按2的倍数进行合并的，但是数据不一定是二的倍数，所以要对右区间的长度进行判断：
●如果右区间左端点已经比n大了，那说明右区间不存在，那就不用归并
●如果只有右区间右端点越界，那就把它修改为（n-1）

最后的memcpy也要注意，因为可能越界，所以不能直接拷贝2*gap个整型大小的空间

void MergeSortNonR(int* a, int n) {int* tmp = (int*)malloc(sizeof(int) * n);int gap = 1;  //每个区间的长度while (gap < n){int index = 0;  //临时数组的下标for (int i = 0; i < n; i += 2 * gap)  //对每一组进行归并{int left1 = i;  //左区间左端点int right1 = left1 + gap - 1;  //左区间右端点int left2 = left1 + gap;  //右区间左端点int right2 = left1 + 2 * gap - 1;  //右区间右端点if (left2 >= n)  //如果右区间的左端点都超出数组范围了，说明右区间不存在break;if (right2 >= n)  //如果右区间右端点越界，那就对它进行修正right2 = n - 1;//放进临时数组while (left1 <= right1 && left2 <= right2){if (a[left1] < a[left2])tmp[index++] = a[left1++];elsetmp[index++] = a[left2++];}//确保剩余元素进入数组while (left1 <= right1){tmp[index++] = a[left1++];}while (left2 <= right2){tmp[index++] = a[left2++];}memcpy(a + i, tmp + i, sizeof(int) *(right2 - i + 1));}gap *= 2;}free(tmp);
}

---

🍉计数排序（了解即可）

额外开一个空间tmp，并初始化为0。遍历序列，遇到某个数，就让额外空间下标对应的元素+1。其实就相当于一块计数板，记录相应的数出现的次数

这么说确实挺抽象的，举个栗子
比如6，1，7，3，9，2，4，6，从6开始遍历：

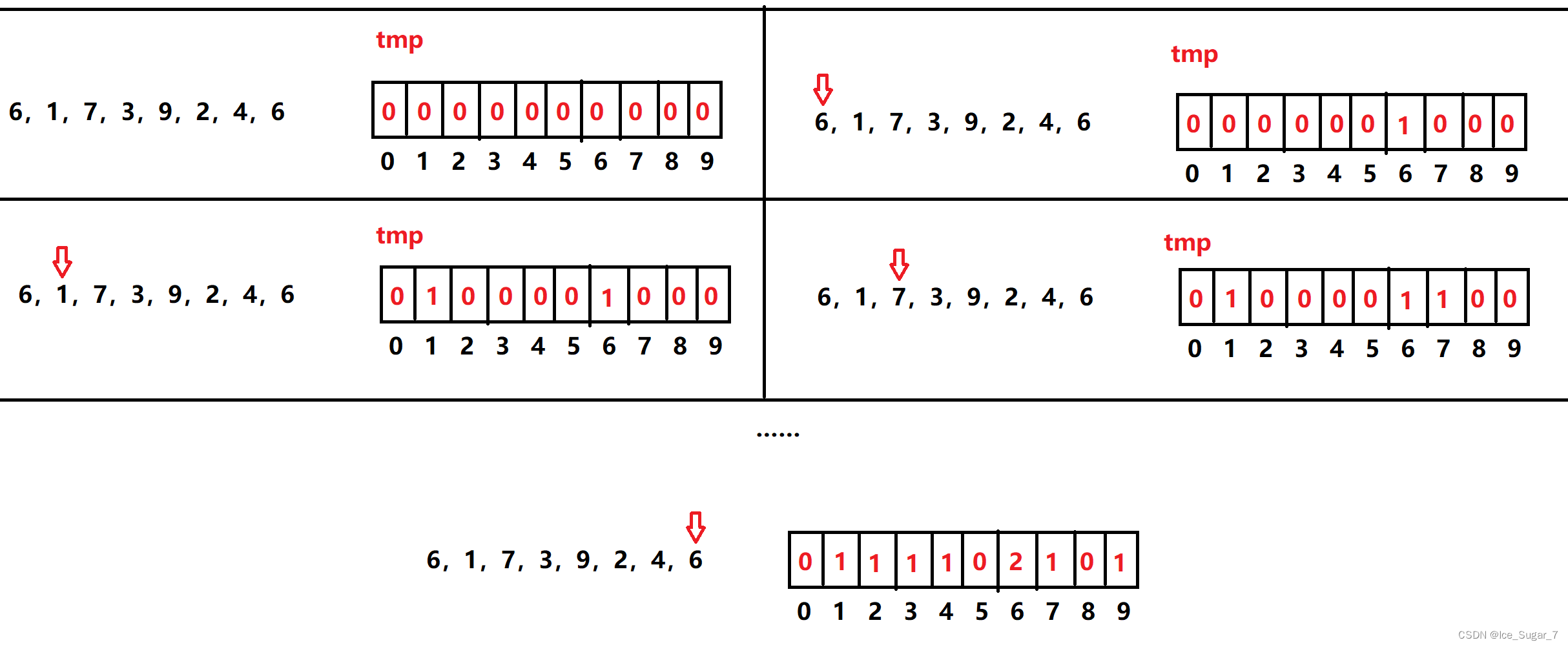
原理很简单：tmp相当于有序序列，遍历完原序列后我们遍历tmp，遇到出现次数不为0的就打印它的下标，出现几次就打印几次，也就可以打印出有序序列了

使用计数排序要先找出序列的最大值、最小值，才能确定tmp下标的范围。比如一个序列最小是100，最大是199，但是数组下标是从0开始的，直接建大小为200的tmp显然浪费空间，所以我们不一定说下标要和数对应，比如0对0,1对1这样子，我们可以0对100,1对101（这种转换数学中称为“映射”）

void CountSort(int* a, int n)
{int min = a[0], max = a[0];for (size_t i = 0; i < n; i++){if (a[i] < min)min = a[i];if (a[i] > max)max = a[i];}int range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);printf("range:%d\n", range);if (count == NULL){perror("malloc fail");return;}memset(count, 0, sizeof(int) * range);// 统计数据出现次数for (int i = 0; i < n; i++){count[a[i] - min]++;}// 排序int j = 0;for (int i = 0; i < range; i++){while (count[i]--){a[j++] = i + min;}}
}