代码随想录算法训练营第28天 | 93.复原IP地址，78.子集，90.子集II

回溯章节理论基础：

https://programmercarl.com/%E5%9B%9E%E6%BA%AF%E7%AE%97%E6%B3%95%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html

93.复原IP地址

题目链接：https://leetcode.cn/problems/restore-ip-addresses/

思路：

这是切割问题，切割问题就可以使用回溯搜索法把所有可能性搜出来，和刚做过的131.分割回文串就十分类似了。

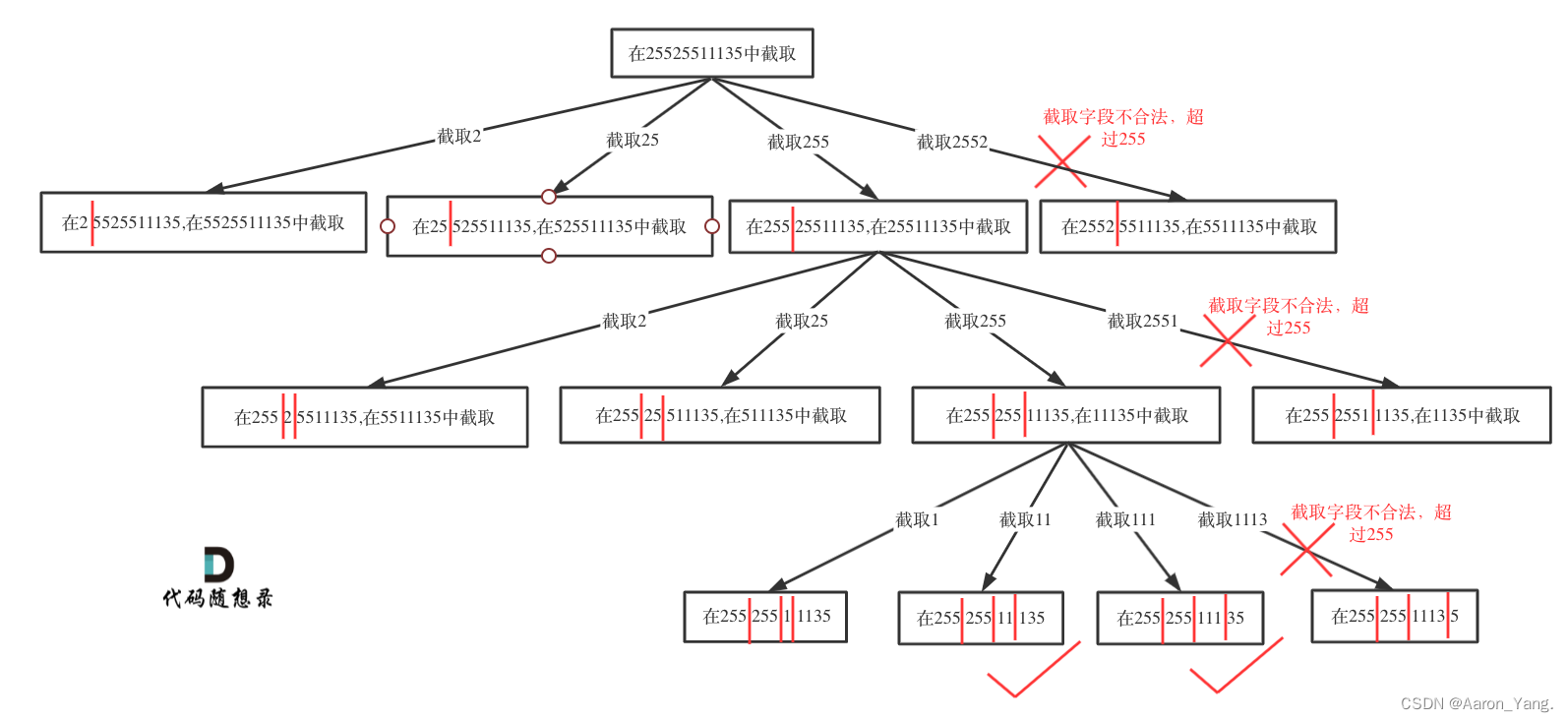
在这里插入图片描述
startIndex一定是需要的，因为不能重复分割，记录下一层递归分割的起始位置。

本题我们还需要一个变量pointNum，记录添加分割点的数量。

终止条件和131.分割回文串 (opens new window)情况就不同了，本题明确要求只会分成4段，所以不能用切割线切到最后作为终止条件，而是分割的段数作为终止条件。

count代表分割点的数量，为3就说明分成4段了。然后验证一下第四段是否合法，如果合法就加入到结果集里。

class Solution {List<String> result = new ArrayList<>();String s;public List<String> restoreIpAddresses(String s) {StringBuilder sb = new StringBuilder(s);backtracking(sb,0,0);return result;}// num代表添加分割点的数量public void backtracking(StringBuilder s, int startIndex, int count){// 终止条件if(count == 3){if(isValid(s,startIndex,s.length()-1))result.add(s.toString());return ;}for(int i= startIndex ; i<s.length() ; i++){if(isValid(s,startIndex,i)){s.insert(i+1, '.');// 还多了一个.backtracking(s,i+2,count+1);s.deleteCharAt(i+1);}elsebreak;}}public boolean isValid(StringBuilder s, int startIndex, int endIndex){if(startIndex > endIndex || endIndex - startIndex > 2)return false;// 把第一个字符是0的情况排除掉 “023”if(s.charAt(startIndex) == '0' && startIndex != endIndex)return false;// 这里不能用int直接转，有可能会超出上界// if(Integer.parseInt(s.toString().substring(startIndex,endIndex+1))<=255)//     return true;int num = 0;for(int i= startIndex;i <= endIndex ; i++){char tmp = s.charAt(i);// 遇到非数字字符不合法if(tmp > '9' || tmp <'0')return false;num = num * 10 + tmp - '0';if(num > 255)return false;}return true;}
}

78.子集

题目链接：https://leetcode.cn/problems/subsets/

思路：

求子集问题和77.组合 (opens new window)和131.分割回文串 (opens new window)又不一样了。

如果把子集问题、组合问题、分割问题都抽象为一棵树的话，那么组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点。

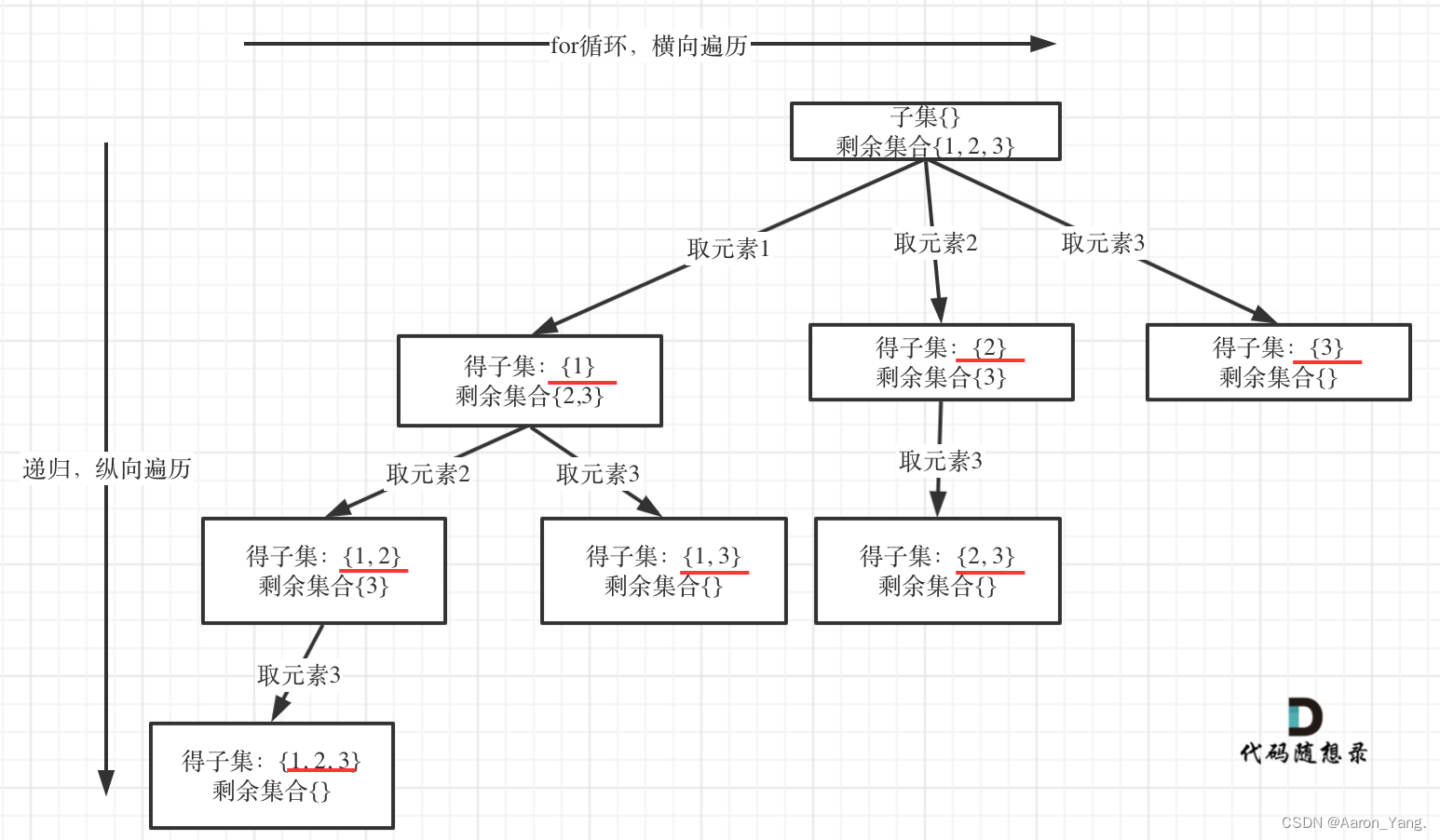
在这里插入图片描述
剩余集合为空的时候，就是叶子节点。

当startIndex已经大于数组的长度了，就终止了，因为没有元素可取了，其实可以不需要加终止条件，因为startIndex >= nums.size()，本层for循环本来也结束了。

同时，求取子集问题，不需要任何剪枝！因为子集就是要遍历整棵树。

class Solution {List<List<Integer>> result = new ArrayList<>();List<Integer> paths = new ArrayList<>();// 这道题和之前的不同之处，不是在叶子结点收获结果了，而是在每一层递归都要进行收获单个结果public List<List<Integer>> subsets(int[] nums) {// 默认情况// result.add(new ArrayList<>(paths));backtracking(nums , 0);return result;}public void backtracking(int[] nums, int startIndex){result.add(new ArrayList<>(paths));if(startIndex >= nums.length)   return ;for(int i= startIndex;i<nums.length;i++){paths.add(nums[i]);backtracking(nums, i+1);// 回溯，比如当遍历到1,2的位置。需要把2回溯，然后才能遍历到1,3paths.removeLast(); }}
}

时间复杂度: O(n * 2^n)
空间复杂度: O(n)

90.子集II

题目链接：https://leetcode.cn/problems/subsets-ii/

思路：

这道题目和78.子集 (opens new window)区别就是集合里有重复元素了，而且求取的子集要去重。

那么关于回溯算法中的去重问题，在40.组合总和II 中已经详细讲解过了，和本题是一个套路。

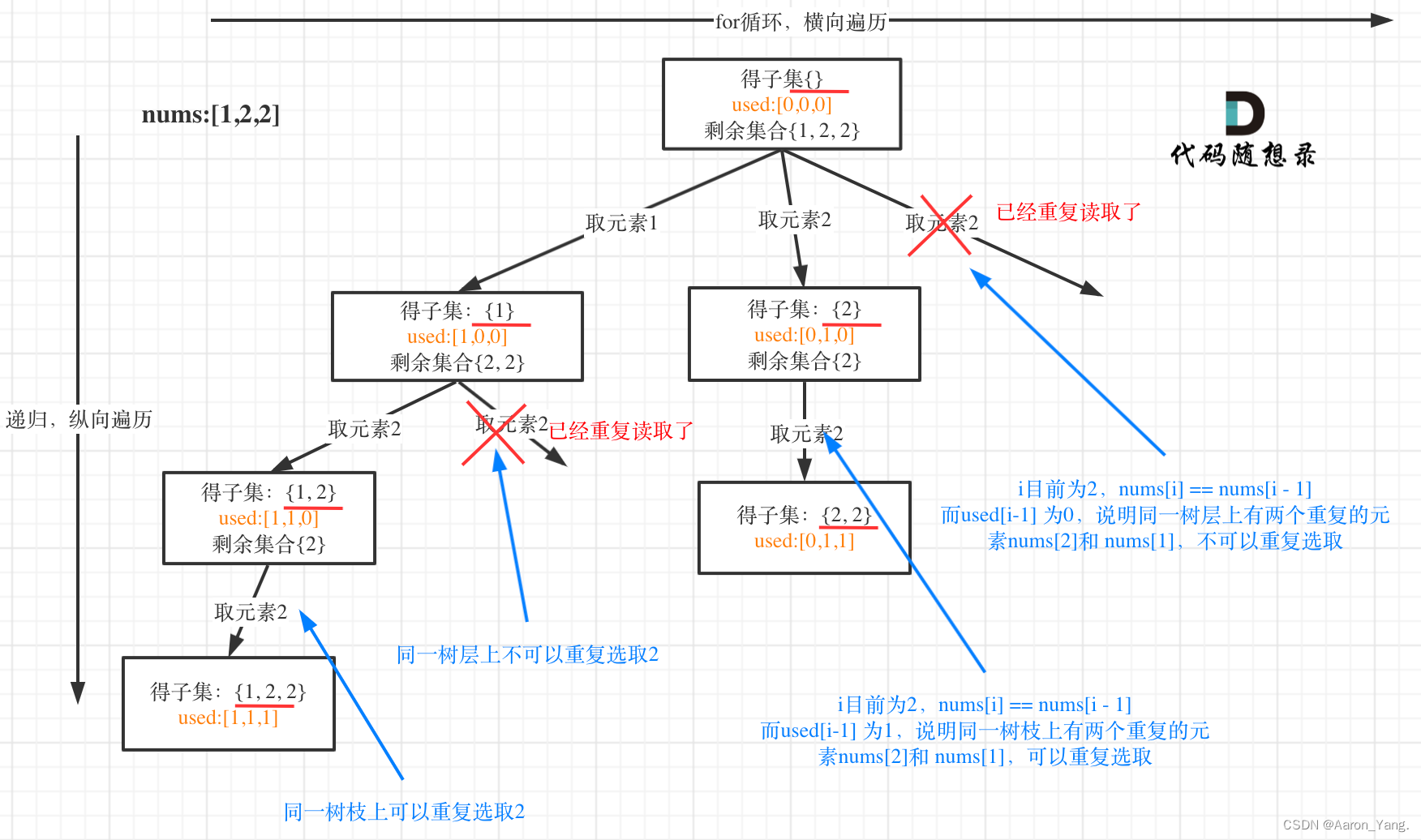
在这里插入图片描述
这里要理解“树层去重”和“树枝去重”！从图中可以看出，同一树层上重复取2 就要过滤掉，同一树枝上就可以重复取2，因为同一树枝上元素的集合才是唯一子集！

class Solution {List<List<Integer>> result = new ArrayList<>();List<Integer> paths = new ArrayList<>();boolean[] used;public List<List<Integer>> subsetsWithDup(int[] nums) {Arrays.sort(nums);used = new boolean[nums.length];Arrays.fill(used,false);// 加入空集，预处理// result.add(new ArrayList<>(paths));backtracking(nums,0);return result;}public void backtracking(int[] nums, int startIndex){result.add(new ArrayList<>(paths));// if(startIndex >= nums.length)   return ;for(int i = startIndex; i < nums.length ;i++){if(i>0 && nums[i] == nums[i-1] && used[i-1] == false){continue ;}paths.add(nums[i]);used[i] = true;backtracking(nums,i+1);paths.removeLast();used[i] = false;}}
}