目录
前言
Prime算法--加点法
acwing-858
代码如下
一些解释
Kruskal算法--加边法
acwing-859
并查集与克鲁斯卡尔求最小生成树
代码如下
一些解释
前言
之前学最短路的时候,我们都是以有向图为基础的,当时我们提到如果是无向图,只要记得两个顶点处都要加边就好了。
而在最小生成树的问题中,我们所面临的大多都是无向图。
这个姐姐👇对这两种算法的讲解非常清晰,没有代码部分,但是对于理解这两种算法的做法很有帮助,推荐看一下。
【数据结构 图 最小生成树 Prime和Kruskal算法】
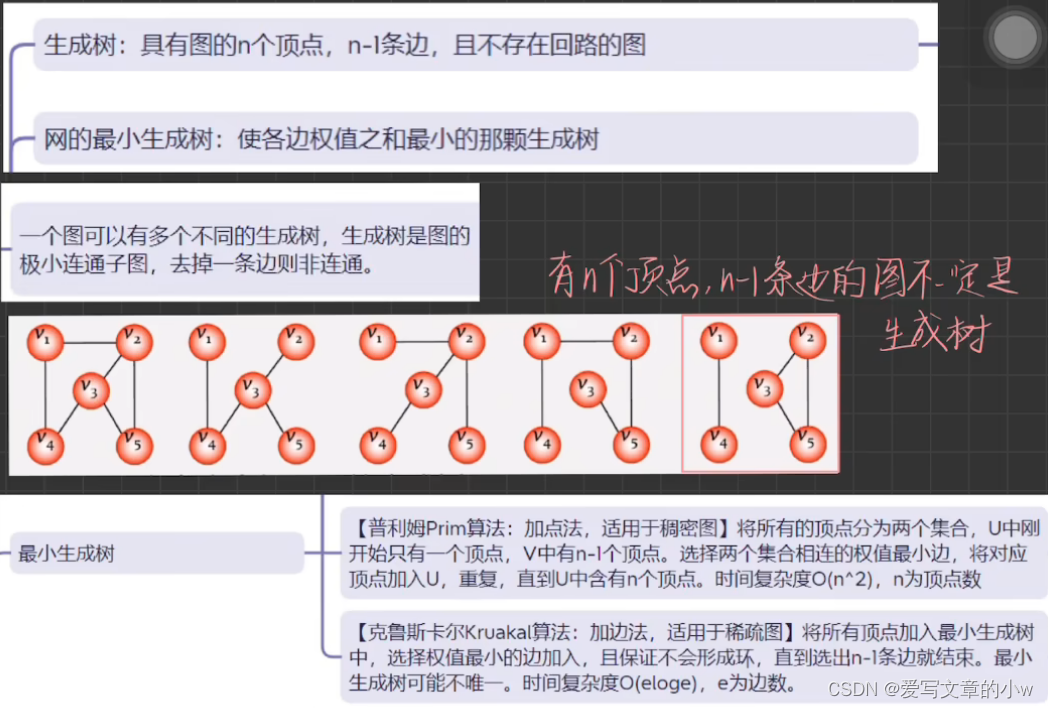
截取自视频。
感觉总结的很好,就搬过来啦(侵删)
Prime算法--加点法
prime算法也叫加点法,主要是通过不断将所有顶点都加入到生成树中实现的。
利用该算法求最小生成树的步骤就是:
从任意1个顶点开始,在其他所有顶点中,选出一个离它距离最近的顶点,将其与该顶点进行连线;之后我们看其他的顶点中 离这两个已经选中的点 之间的距离最短的点,再将其连线......
由此我们可以总结出,我们要看的是:其他顶点中 到已经选出的这些顶点的集合 距离最短的点,我们把这个集合称为生成树,这里可以理解哈。
因此我们可以判断dist数组的含义应该是:存储每一个顶点到 集合(也就是生成树) 的最短距离。
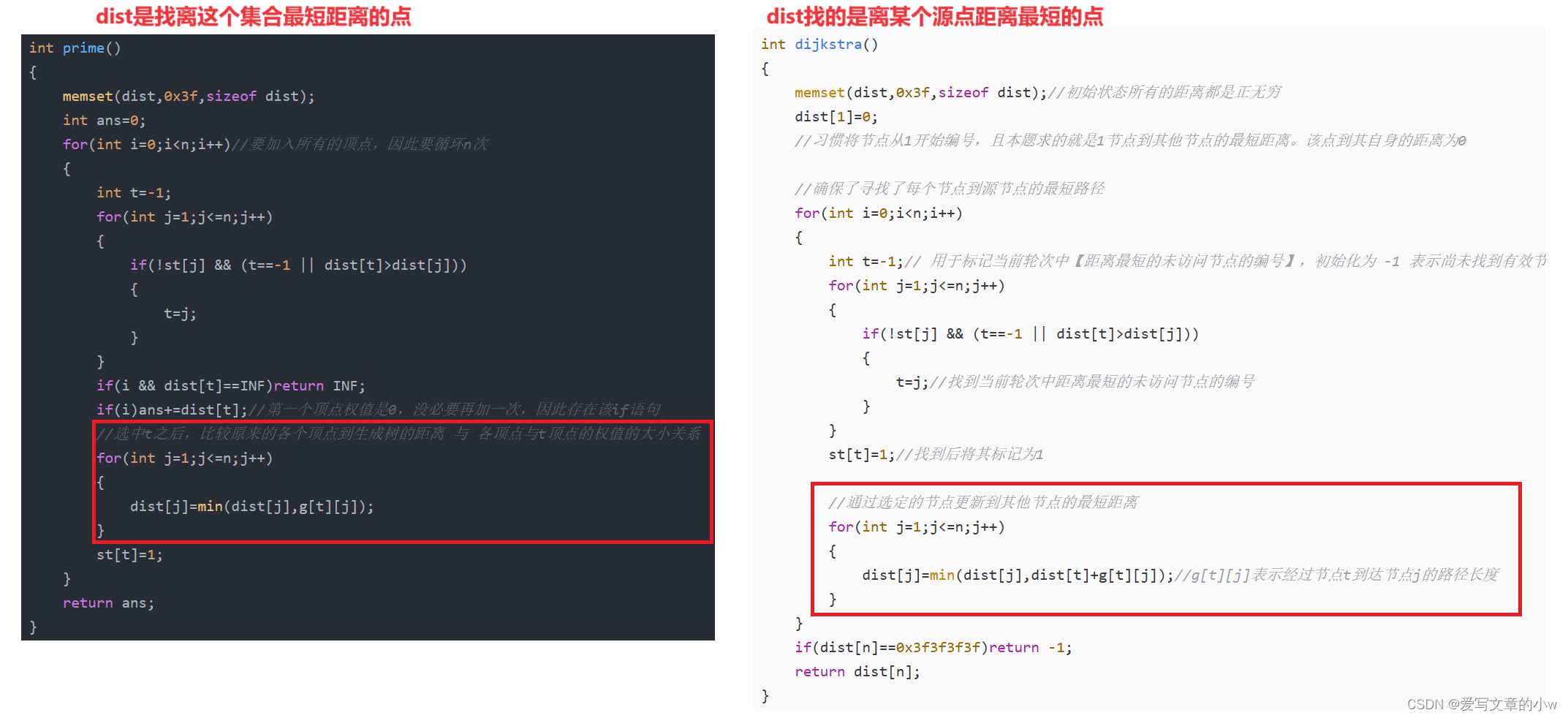
prime算法的代码和dijkstra算法的实现是差不多的,主要区别就是dist数组的含义。前者是找离这个集合最短距离的点,后者找的是离某个源点距离最短的点。
下面这个图模拟我们prime算法的手算的步骤
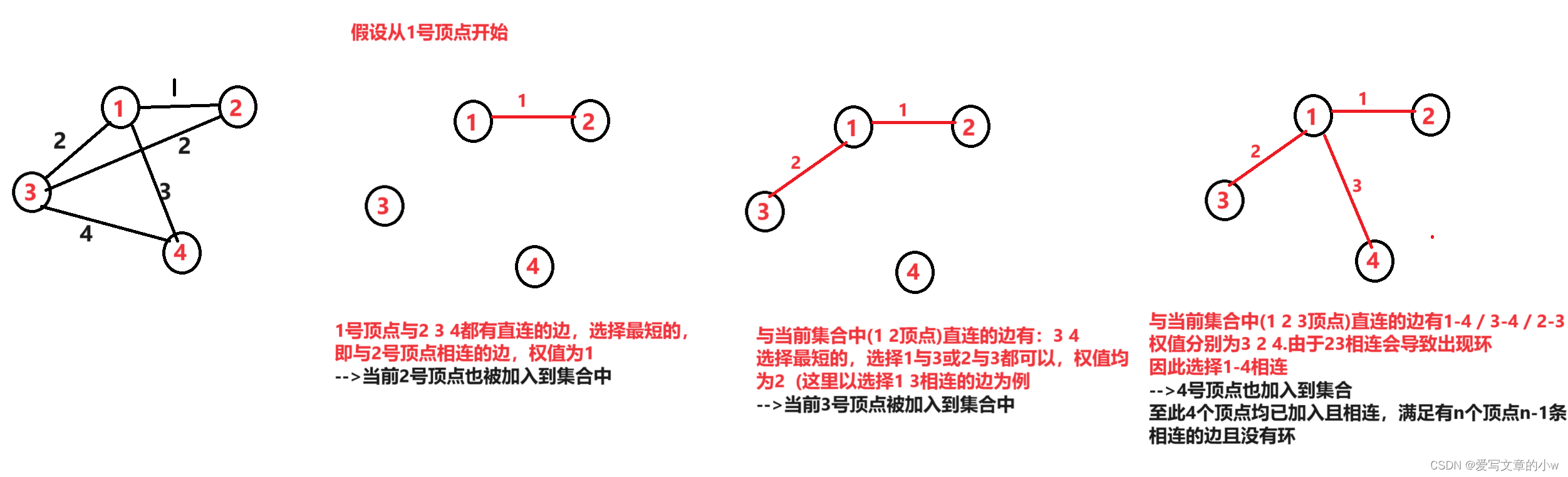
方便大家理解啦~
prime算法时间复杂度是O(n^2),适用于解决稠密图的问题。
下面是模板题:
acwing-858
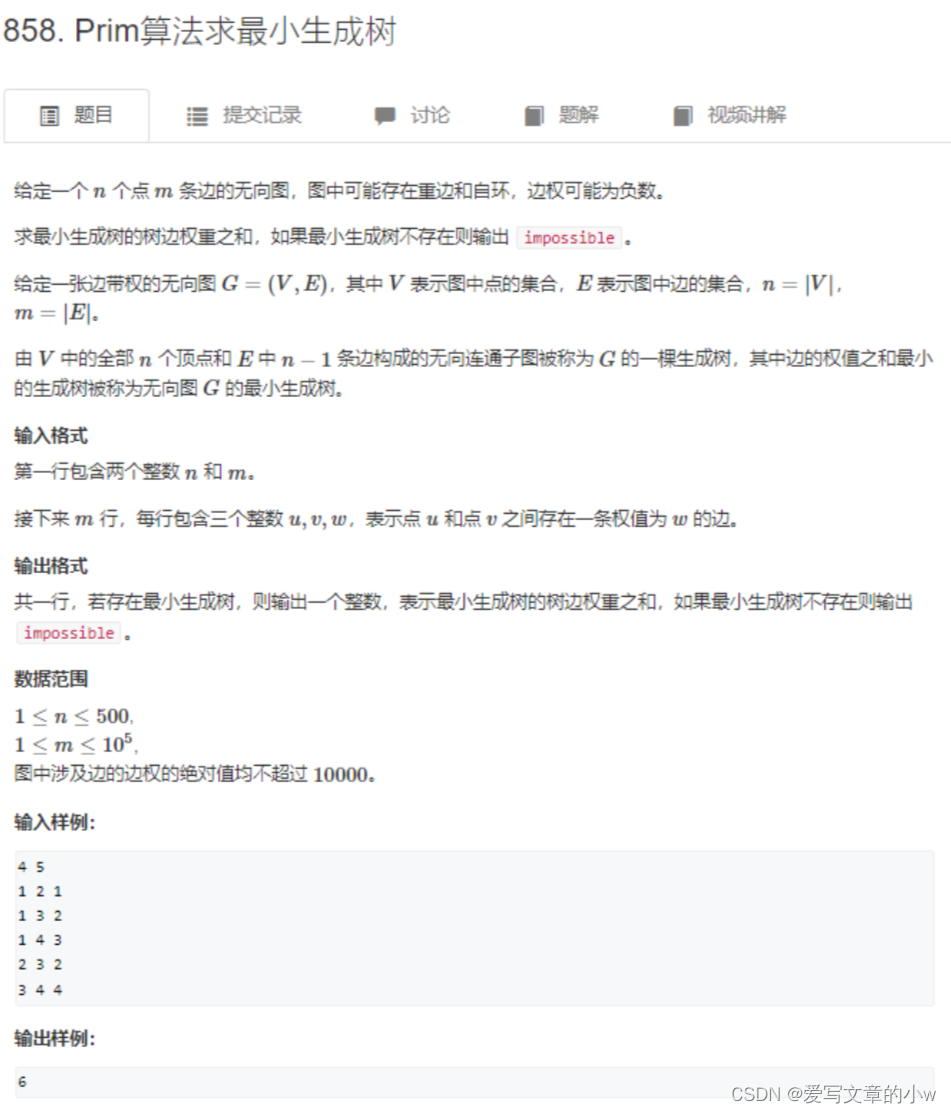
可以看出数据范围边数远大于点数,属于稠密图。
与dijkstra算法的思路是差不多的,直接看代码把
代码如下
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=510, INF=0x3f3f3f3f;
int n,m;
int g[N][N];
int dist[N];//存储每一个顶点到 集合(也就是生成树) 的最短距离
bool st[N];
int prime()
{memset(dist,0x3f,sizeof dist);int ans=0;for(int i=0;i<n;i++)//要加入所有的顶点,因此要循环n次{int t=-1;for(int j=1;j<=n;j++){if(!st[j] && (t==-1 || dist[t]>dist[j])){t=j;}}if(i && dist[t]==INF)return INF;if(i)ans+=dist[t];//第一个顶点权值是0,没必要再加一次,因此存在该if语句//选中t之后,比较原来的各个顶点到生成树的距离 与 各顶点与t顶点的权值的大小关系for(int j=1;j<=n;j++){dist[j]=min(dist[j],g[t][j]);}st[t]=1;}return ans;
}
int main()
{cin>>n>>m;memset(g,0x3f,sizeof g);for(int i=0;i<m;i++){int a,b,c;cin>>a>>b>>c;g[a][b]=g[b][a]=min(g[a][b],c);}int t=prime();if(t==INF)puts("impossible");else cout<<t<<endl;return 0;
}一些解释
1.if(i && dist[t]==INF)return INF;
这里我们判断除了第一个顶点之外的其他顶点,到生成树的距离是否是无穷大,如果是无穷大说明图不连通,无法构成生成树。
由于我们外层循环只控制循环次数,表示要加入n个顶点,且i从0开始,说明了第一个顶点是作为第0次循环实现的,因此这里排除第一个顶点,直接判断 i 就可以
为什么要跳过第一个顶点?
如果我们不跳过第一个顶点,那么在第一次循环时,由于所有顶点到生成树的距离都被初始化为无穷大,所以会直接返回无穷大,这显然是不正确的。因此,我们需要在第一次循环时跳过这个检查。
2.dist[j]=min(dist[j],g[t][j]);
这里遍历各个顶点,判断 其原始的dist[j]与添加了 t 顶点之后,t与j顶点之间的权值 的大小关系,从而更新出每个顶点到生成树的距离。(因为既然t已经被加入到生成树中,那么到t的权值也就是到生成树的距离啦。)
把prime与dijkstra的代码放在一起对比一下
Kruskal算法--加边法
kruskal算法与prime对应是加边法,主要通过不断加边,连接到所有顶点之后就得到了最小生成树。
利用这种方法求最小生成树的步骤是:
在所有的边中不断的找最小的边加入到我们最小生成树的集合中,直到将所有顶点都连入。在加边过程中,避免成环即可。
曾经学数据结构的时候,手算我还是比较喜欢用克鲁斯卡尔算法的哈哈哈,感觉加边理解上好像更简单一点。
acwing-859

并查集与克鲁斯卡尔求最小生成树
我们记得在并查集算法中,进行两个集合的合并和查找操作,就是利用树型结构实现的,在克鲁斯卡尔算法求最小生成树时,我们最终就是将顶点都连在一起算是得到了最小生成树,因此我们可以想着利用并查集的思想来实现克鲁斯卡尔求最小生成树。
嗯,,可以想一下二者的联系。我通过这样可以理解二者的关联。
下面是gpt的解释,更全面和专业一点hh,可以看看帮助理解一下~

应该是可以理解啦。
需要的话可以回顾一下并查集的知识,之前写过哒
【第十四课】并查集(acwing-837连通块中点的数量 / c++代码 / 思路详解)
代码如下
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=2e5+10;
int n,m;
int p[N];
struct Edge{int a,b,w;//运算符重载函数bool operator< (const Edge &W)const{return w<W.w;}
}edges[N];
int find(int x)
{if(p[x]!=x)p[x]=find(p[x]);return p[x];
}
int main()
{cin>>n>>m;for(int i=0;i<m;i++){int a,b,w;cin>>a>>b>>w;edges[i]={a,b,w};}sort(edges,edges+m);//每个顶点都单独处在一个集合里for(int i=1;i<=n;i++)p[i]=i;int res=0,count=0;//res累加权值 count存储加入的边数for(int i=0;i<=m;i++)//遍历排好序的边的信息{int a=edges[i].a,b=edges[i].b,w=edges[i].w;a=find(a),b=find(b);//如果该边的两个顶点不连通 说明不会形成环if(a!=b){p[a]=b;res+=w;count++;}}if(count<n-1)puts("impossible");//如果边数并不符合 说明不存在最小生成树else cout<<res;return 0;
}一些解释
sort(edges,edges+m);这里我们调用sort函数,直接写的edge结构体-edge+m,就是因为在结构体中我们定义了重载
//运算符重载函数bool operator< (const Edge &W)const{return w<W.w;}因为结构体中含有多个变量,如果不定义运算符重载,那么在使用 sort 函数等需要比较边的权值大小的地方,编译器将无法确定如何比较两个 Edge 对象 。
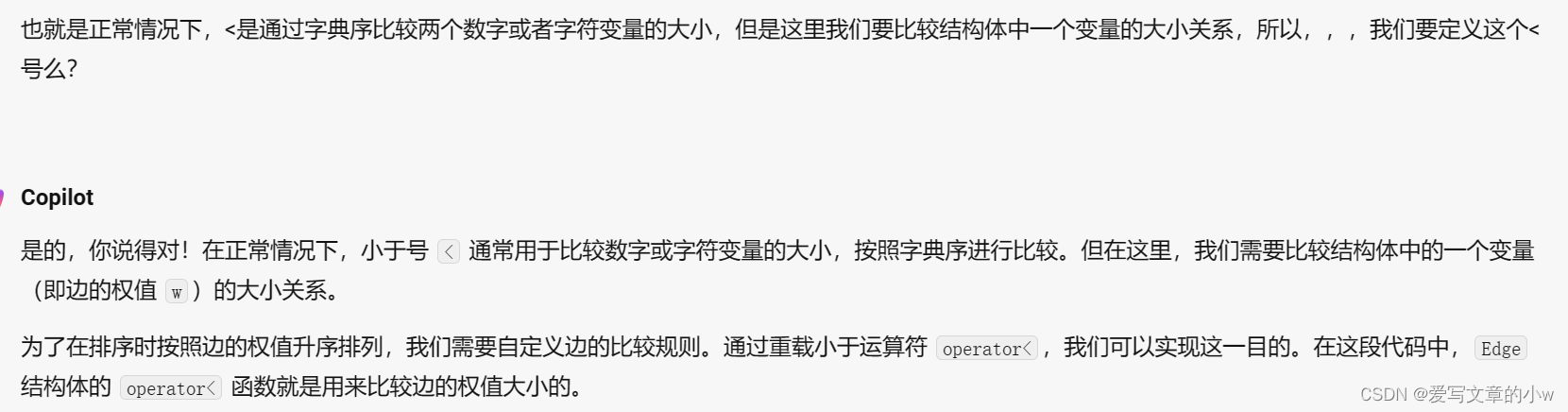

关于重载的一些知识,,,

今年就先写到这里啦。大家除夕快乐啦~
有问题欢迎指出,一起加油!!