决策树
文章目录
- 决策树
- 1 决策树学习基础
- 2 经典决策树算法
- 3 过拟合问题
1 决策树学习基础
-
适用决策树学习的经典目标问题
- 带有非数值特征的分类问题
- 离散特征
- 没有相似度概念
- 特征无序
例子:
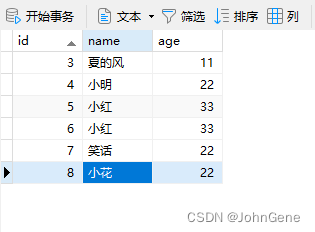
Sky Temp Humid Wind Water Forecast Enjoy Sunny Warm Normal Strong Warm Same Yes Sunny Warm High Strong Warm Same Yes Rainy Cold High Strong Warm Change No Sunny Warm High Strong Cool Change Yes -
样本表示:属性的列表而非数值向量
-
决策树概念
- 分枝:特征/属性的取值
- 非叶子节点:特征/属性
- 叶子节点:决策/标签/类别/概念
2 经典决策树算法
-
ID3算法
ID3算法是一种用来构造决策树的贪心算法,它是一种监督学习的方法,可以用来进行分类预测。
- 自顶向下,贪心搜索,递归算法
- 核心循环
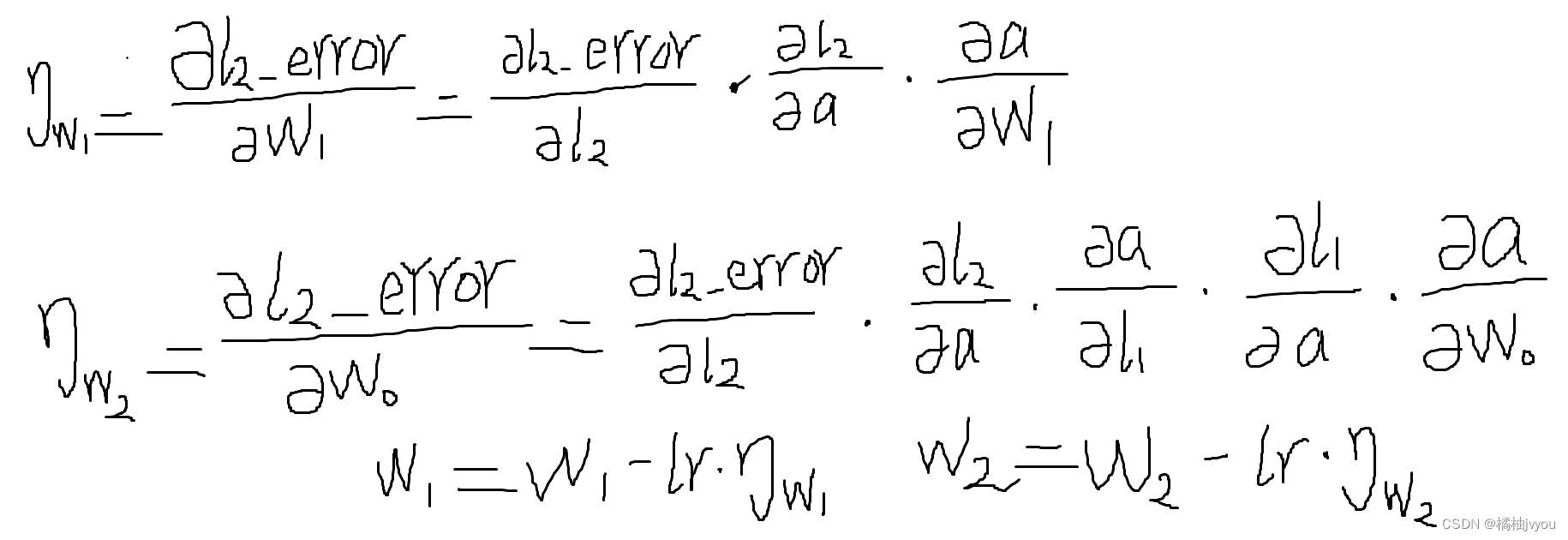
- A A A :下一步 最佳 决策属性
- 将 A A A 作为当前节点决策属性
- 对属性 A ( v i ) A (v_i ) A(vi)的每个值,创建与其对应的新的子节点
- 根据属性值将训练样本分配到各个节点
- 如果 训练样本被完美分类,则退出循环,否则继续下探分裂新的叶节点
-
当前最佳属性节点选择
-
基本原则:简洁——我们偏向于使用简洁的具有较少节点的树
-
属性选择和节点混杂度(Impurity)
在每个节点 N上,我们选择一个属性 T,使得到达当 前派生节点的数据尽可能 “纯”
-
熵(Entropy)
E n t r o p y ( N ) = − ∑ j P ( w j ) l o g 2 P ( w j ) Entropy(N)=-\sum_jP(w_j)log_2P(w_j) Entropy(N)=−j∑P(wj)log2P(wj)
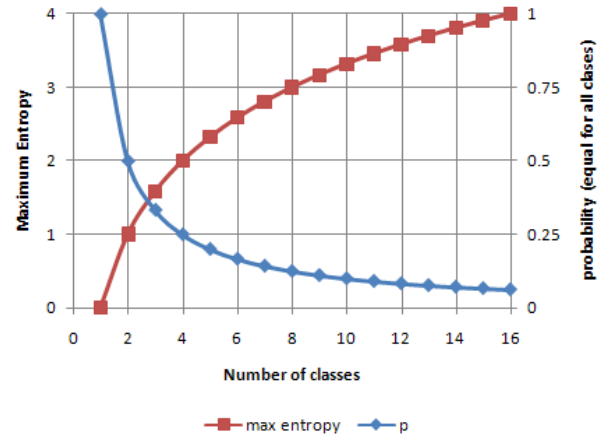
定义: 0 l o g 0 = 0 0log0=0 0log0=0在信息理论中,熵度量了信息的纯度/混杂度,或者信息的 不确定性
正态分布 – 具有最大的熵值
-
Gini 混杂度
i ( N ) = 1 − ∑ i P 2 ( w j ) i(N)=1-\sum_iP^2(w_j) i(N)=1−i∑P2(wj)
最大 Gini 混杂度 在 1 − n ∗ ( 1 / n ) 2 = 1 − 1 / n 1-n*(1/n)^2=1-1/n 1−n∗(1/n)2=1−1/n 时取得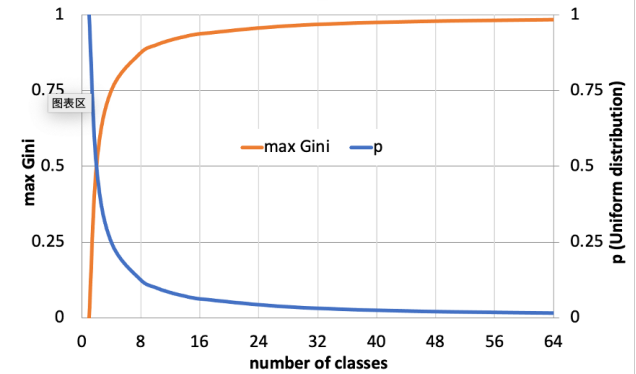
-
错分类混杂度
i ( N ) = 1 − m a x j P ( w j ) i(N)=1-max_jP(w_j) i(N)=1−maxjP(wj)
在有n类时,最大错分类混杂度 = 最大Gini混杂度 1 − m a x ( 1 / n ) = 1 − 1 / n 1-max(1/n)=1-1/n 1−max(1/n)=1−1/n
-
-
信息增益(IG)——度量混杂度的变化ΔI(N)
由于对A的排序整理带来的熵的期望减少量
G a i n ( S , A ) = E n t r o p y ( S ) − ∑ v ∈ V a l u e s ( A ) ∣ S v ∣ ∣ S ∣ E n t r o p y ( S v ) Gain(S,A)=Entropy(S)-\sum_{v∈Values(A)}\frac{|S_v|}{|S|}Entropy(S_v) Gain(S,A)=Entropy(S)−v∈Values(A)∑∣S∣∣Sv∣Entropy(Sv)
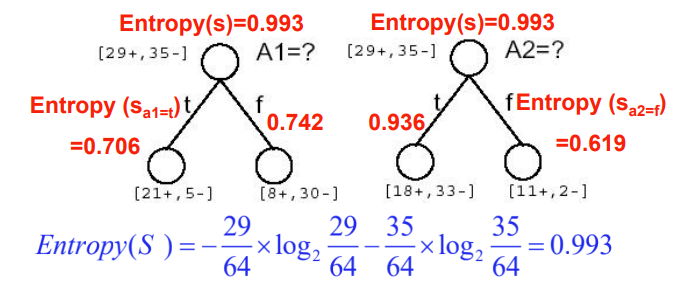
-
-
停止分裂节点
-
如果当前子集中所有数据 有完全相同的输出类别,那么终止
①有噪声、②漏掉重要Feature
-
如果当前子集中所有数据 有完全相同的输入特征,那么终止
-
-
假设空间
- 假设空间是完备的——目标函数一定在假设空间里
- 输出单个假设——不超过20个问题(根据经验)
- 没有回溯——局部最优
- 在每一步中使用子集的所有数据——数据驱动的搜索选择,对噪声数据有鲁棒性
-
归纳偏置(Inductive Bias)
- 无假设空间限制——假设空间 H 是作用在样本集合 X 上的
- 有搜索偏置——偏向于在靠近根节点处的属性具有更大信息增益的树(奥卡姆剃刀)
-
CART (分类和回归树)
- 根据训练数据构建一棵决策树
- 决策树会逐渐把训练集合分成越来越小的子集
- 当子集纯净后不再分裂
- 或者接受一个不完美的决策
-
ID3算法基本流程
- 从根节点开始,计算所有可能的特征的信息增益,选择信息增益最大的特征作为节点的划分特征;
- 由该特征的不同取值建立子节点;
- 再对子节点递归上述步骤,构建决策树;
- 直到没有特征可以选择或类别完全相同为止,得到最终的决策树。
3 过拟合问题
-
定义
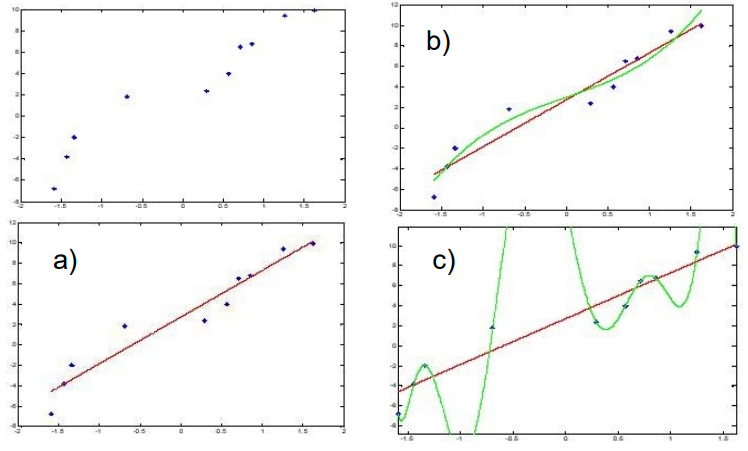
a. 真实数据,b. 非过拟合结果,c. 过拟合结果
当 h ∈ H h∈H h∈H 对训练集过拟合,如果 存在另一个假设 h ’ ∈ H h’ ∈H h’∈H 满足: e r r t r a i n ( h ) < e r r t r a i n ( h ′ ) A N D e r r t e s t ( h ) > e r r t e s t ( h ′ ) err_{train}(h)<err_{train}(h')\ AND\ err_{test}(h)>err_{test}(h') errtrain(h)<errtrain(h′) AND errtest(h)>errtest(h′)
例子:每个叶节点都对应单个训练样本 —— 每个训练样本都被完美地分类(查表)
-
解决方案——如何避免过拟合
-
预剪枝——当数据的分裂在统计意义上并不显著时,就停止增长
-
基于样本数:通常 一个节点不再继续分裂,当到达一个节点的训练样本数小于训练集合的一个特定比例 (%5),无论混杂度或错误率是多少都停止分裂
原因:基于过少数据样本的决定会带来较大误差和泛化错误
-
基于信息增益的阈值:设定一个较小的阈值,如果满足 Δ i ( s ) ≤ β Δi(s)≤\beta Δi(s)≤β 则停止分裂
优点:用到了所有训练数据;叶节点可能在树中的任何一层
缺点:很难设定一个好的阈值
-
-
后剪枝——构建一棵完全树,然后再剪枝
-
错误降低剪枝:剪枝直到再剪就会对损害性能
把数据集分为训练集和验证集,在验证集上测试剪去每个可能节点(和以其为根的子树)的影响
贪心地去掉某个可以提升验证集准确率的节点
-
规则后剪枝:
- 把树转换成等价的由规则构成的集合
- 对每条规则进行剪枝,去除哪些能够提升该规则准确率的规则前件
- 将规则排序成一个序列 (根据规则的准确率从高往低排序)
- 用该序列中的最终规则对样本进行分类(依次查看是否满足规则序列)
注:在规则被剪枝后,它可能不再能恢复成一棵树
-
-