目录

前言

导入numpy并初始化数据和激活函数

初始化学习率和模型参数 

迭代更新模型参数（权重）

小彩蛋

---

前言

这篇文章，小编带大家使用python-numpy实现一个简单的三层神经网络，不使用pytorch等深度学习框架，来理解一下神经网络的原理和观察一下它内部的一些操作如反向传播，权重更新是如何实现的。

导入numpy并初始化数据和激活函数

# 三层神经网络
import numpy as npdef sigmoid(x, back=False):  # 激活函数if back:return x * (1 - x)  # 反向传播（求了个导）return 1 / (1 + np.exp(-x))  # 前向传播x = np.array([[0, 0, 1],[0, 1, 1],[1, 0, 1],[1, 1, 1],[0, 0, 1]]
)
print(x.shape)  # 构造出来五个样本，每个样本有三列特征
y = np.array([[0],[1],[1],[0],[0]]
)
print(y.shape)  # 构造目标值，有监督学习

在这里我们先定义了一个激活函数，这里用sigmoid激活函数，激活函数用于加在每层网络的后面，使得神经网络可以进行非线性变换。

我们同时又用numpy创建了一个输入x和标签（输出）y，x为五个样本，每个样本有三个特征值，y是x对应五个样本的输出，在这里我们进行一个二分类，所以y中的值只有0或者1。

初始化学习率和模型参数 

np.random.seed(1)  # 指定随机种子，使得每次程序的随机数都一样
lr = 0.1 # 初始化学习率
w0 = 2 * np.random.random(size=(3, 4)) - 1  # 随机生成变换矩阵
w1 = 2 * np.random.random(size=(4, 1)) - 1  # 和w0相呼应，1是输出的意思，这里不是输出1就是输出0

在这里我们初始化学习率为0.1，这个数值是控制模型参数每次更新步长的超参数，学习率过大会使得模型震荡，学习率过小会使得模型收敛速度较慢。

w0和w1为模型参数，也是模型要学习的数值，通过不断迭代以最小化损失函数为目的会使得这两个数值不断更新。（使用深度学习框架编写神经网络时，权重的初始化会由框架实现，其是随机初始化）

此时我们的网络就是这个样子的

迭代更新模型参数（权重）

模型参数的更新主要有这几个过程：

1，通过x和随机的模型参数进行前向传播，得到预测的y。

2，通过预测得到的y和真实的y进行计算，获得损失函数。

3，通过损失函数反向传播，利用链式法则获得梯度，从而根据学习率和梯度去更新模型参数。

这几步为神经网络的核心，其旨在不断迭代，从而使得我们可以获得一组模型参数，通过这组模型参数，我们就可以使得输入x后得到的结果最大程度的接近真实的y值。

for j in range(60000):  # 神经网络计算# 前向传播l0 = x  # 定义神经网络第一层（输入层），直接等于xl1 = sigmoid(np.dot(l0, w0))  # 矩阵相乘（注意顺序），别忘了乘激活函数l2 = sigmoid(np.dot(l1, w1))l2_error = (l2 - y) ** 2 / 2  # 误差项（均方误差损失函数）# 反向传播l2_delta = (l2 - y) * sigmoid(l2, back=True)l1_error = np.dot(l2_delta, w1.T)l1_delta = l1_error * sigmoid(l1, back=True)# 更新权重w1 -= lr * np.dot(l1.T, l2_delta)w0 -= lr * np.dot(l0.T, l1_delta)# 验证误差if j % 10000 == 0:print('ERROR: '+str(np.mean(l2_error)))

这里附上运行结果和链式法则的图片

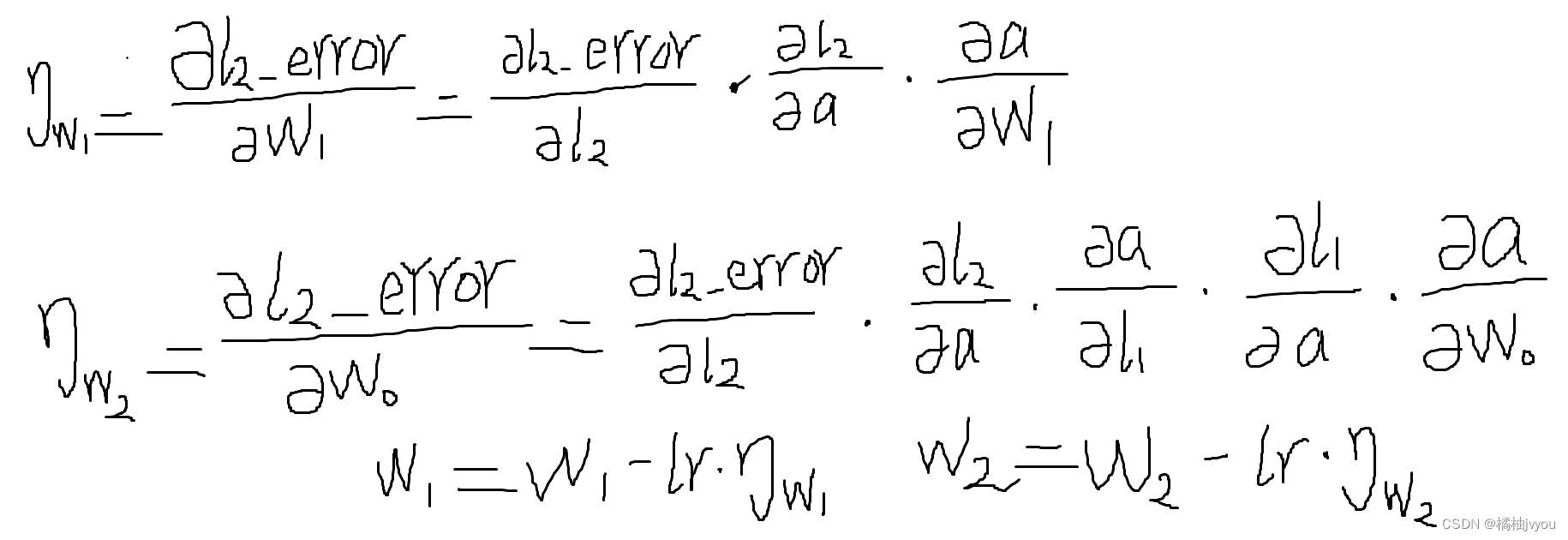
 其中，a为经过sigmoid激活函数得到的结果，图片中的w2为代码里的w0

小彩蛋

最后附上一个类比来更加形象的理解神经网络的运作原理与步骤。

我们可以将神经网络类比为去商场买衣服，那么为什么可以这么理解呢，小编在这里给出解释，括号里为对应的神经网络中的操作。

假设你去商场买衣服，那么你肯定想要一件合身且好看的衣服（在这里你为输入x，你的满意程度为输出y，而衣服就是中间的模型参数），那么你刚进商城，你肯定不知道那件衣服适合你，此时你就会根据初步的印象来选择一件衣服去试一下（初始化模型参数），你试过之后，你就会获得一个满意程度（获得损失函数），此时你也知道你试的这件是大了还是小了，你知道下一件试衣服是该试大的还是小的（根据损失函数反向传播），然后你会根据这个信息去试下一件（更新模型参数），而在这里比方说你试的衣服大了，那么你下一件肯定会去拿稍微小的衣服，但是具体小多少呢，这个在日常生活中应该会估计一下（在神经网络中，具体小多少这件事情就是学习率做的事），最后通过不断的试穿衣服，我们会找到最合适的那身最后买下（不断迭代使得损失函数最小化）。

那么还有一个疑问，损失函数去哪里了呢，损失函数可以理解为你换衣服的过程，比如这件你感觉很合适，但是试来试去你发现并不合你的身，那么此时你会去试其他不同的衣服（这在神经网络中就是损失函数的作用）。

视频讲解请查看：https://www.bilibili.com/video/BV1pK421C7xr/?spm_id_from=333.999.0.0&vd_source=ea64b940c4e46744da2aa737dca8e183