1.题目

给定一个包含 $n$个点（编号为 $1\sim n$）的无向图，初始时图中没有边。

现在要进行 $m$ 个操作，操作共有三种：

1. C a b，在点 a 和点 b 之间连一条边，a 和 b 可能相等；
2. Q1 a b，询问点 a 和点 b 是否在同一个连通块中，a 和 b 可能相等；
3. Q2 a，询问点 a 所在连通块中点的数量；

输入格式
第一行输入整数 $n$ 和 $m$。

接下来 $m$ 行，每行包含一个操作指令，指令为 C a b，Q1 a b 或 Q2 a 中的一种。

输出格式
对于每个询问指令 Q1 a b，如果 $a$和 $b$ 在同一个连通块中，则输出 Yes，否则输出 No。

对于每个询问指令 Q2 a，输出一个整数表示点 $a$ 所在连通块中点的数量

每个结果占一行。

数据范围
$1\le n,m\le 10^5$

输入样例：

5 5
C 1 2
Q1 1 2
Q2 1
C 2 5
Q2 5

输出样例：

Yes
2
3

2.基本思想

因为与合并题目中唯一不同的是，多了记录合并集合中连通块的个数
通过size数组记录以当前点x为祖先节点的集合中的连通块个数

for(int i = 0; i <= n; i ++) {p[i] = i;//用祖先节点记录当前合并集合的sizesize[i] = 1;
}

初始化，让自己指向自己，同时标记自己为祖先节点下,有多少个连通块，初始为1

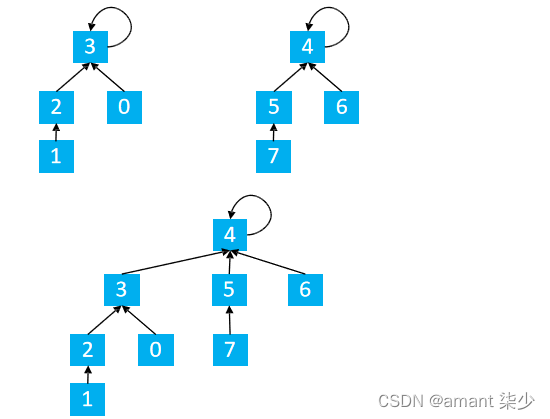
显然，将1,5合并
find(1) = 3 find(5) = 4
p[3] = 4
这时候有8个点相连接
合并的数目更新方式:
size[3] = 4 以3为根节点下有4个连通块
size[4] = 4 以4为根节点下有4个连通块
更新4节点的连通块情况
size[4] = size[4] + size[3] = 8

3.代码实现

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;public class Main {static int N = 100010;static int[] size = new int[N], p = new int[N];public static void main(String[] args) throws IOException {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));String[] s = br.readLine().split(" ");int n = Integer.parseInt(s[0]);for (int i = 0; i < n; i++) {p[i] = i;//最开始 初始化size[i] = 1;}int m = Integer.parseInt(s[1]);while (m-- > 0) {//m 次操作String[] s1 = br.readLine().split(" ");String opt = s1[0];if (opt.equals("C")) {int a = Integer.parseInt(s1[1]), b = Integer.parseInt(s1[2]);if (find(a)==find(b)) continue;size[find(b)] += size[find(a)];p[find(a)] = find(b);} else if (opt.equals("Q1")) {int a = Integer.parseInt(s1[1]), b = Integer.parseInt(s1[2]);System.out.println(find(a) == find(b) ? "Yes" : "No");} else if (opt.equals("Q2")) {int a = Integer.parseInt(s1[1]);System.out.println(size[find(a)]);}}}private static int find(int x) {if (p[x] != x) p[x] = find(p[x]);return p[x];}
}