Linux运用fork函数创建进程

fork函数：

函数原型：

pid_t fork(void);

父进程调用fork函数创建一个子进程，子进程的用户区父进程的用户区完全一样，但是内核区不完全一样；如父进程的PID和子进程的PID不一样。

返回值：

RETURN VALUEOn success, the PID of the child process is returned in the parent, and0  is returned in the child.  On failure, -1 is returned in the parent,no child process is created, and errno is set appropriately.

父进程返回的是子进程的PID,这个值大于0。

子进程返回的是0。

注意：一个进程只能返回一个值，父子进程各自返回一个值。

父进程执行pid>0的逻辑，子进程执行pid==0的逻辑；

父子进程谁先执行：谁先抢到cpu时间片，谁先执行。

这是fork.c文件：

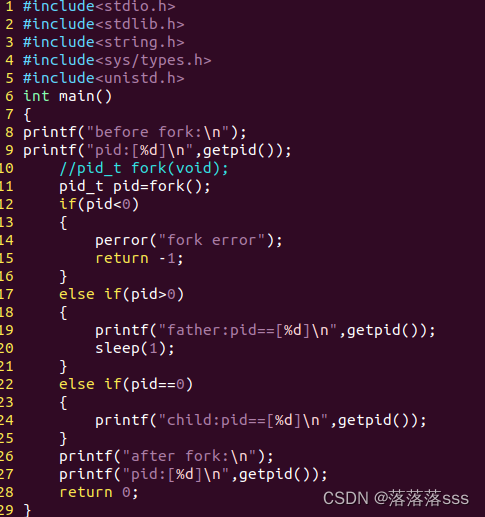
通过fork函数创建了一个子进程。

pid也获得了两个值，一个大于零（父进程），一个等于零（子进程）。

两个进程都会执行下面的语句。

父进程执行时，pid>0,会打印出"father:pid==[%d]\n"

子进程执行时，pid=0,会打印出"child:pid==[%d]\n"

在父进程处加sleep（1）是防止父进程比子进程提前结束，让子进程变成孤儿进程。

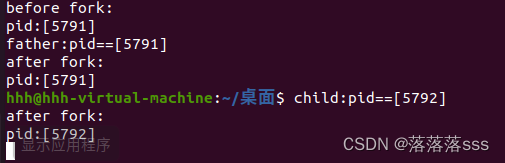
执行后：

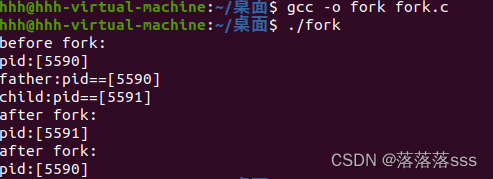
去掉sleep后有两种结果，一种是子进程先结束：

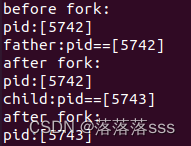
一种是父进程先结束，子进程变孤儿进程，返回命令句：

如何创建兄弟进程：

通过以上操作创建的子进程不是全部是兄弟进程，就创建出七个子进程（子进程也会创建子进程）。我们可以添加break;如果是子进程，就跳出循环，不让他创建自己的子进程。

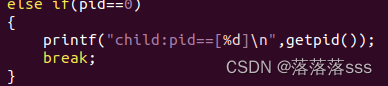
再添加以下操作就可以知道是第几个进程

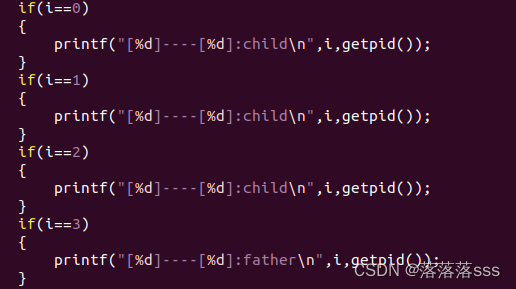
父进程中i会增到3，所以i==3时是父进程。

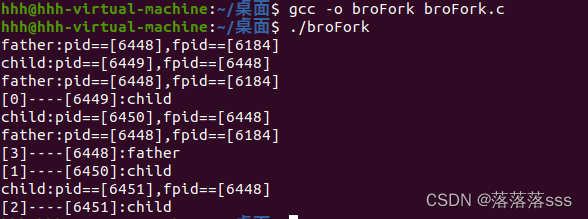
完整代码：

#include<stdio.h>2 #include<stdlib.h>3 #include<string.h>4 #include<sys/types.h>5 #include<unistd.h>6 int main()7 {8 9     //pid_t fork(void);10     int i=0;11     for(;i<3;i++)12     {13         pid_t pid=fork();14         if(pid<0)15         {16             perror("fork error");17             return -1;18         }19         else if(pid>0)20         {21             printf("father:pid==[%d],fpid==[%d]\n",getpid(),getppid());22             //sleep(1);23         }24         else if(pid==0)25         {26             printf("child:pid==[%d],fpid==[%d]\n",getpid(),getppid());break;27         }28         //  else if(pid>0)29         //  {30         //      printf("father:pid==[%d]\n",getpid());31         //  }32     }33     if(i==0)34     {35         printf("[%d]----[%d]:child\n",i,getpid());36     }37     if(i==1)38     {39         printf("[%d]----[%d]:child\n",i,getpid());40     }41     if(i==2)42     {43         printf("[%d]----[%d]:child\n",i,getpid());44     }45     if(i==3)46     {47         printf("[%d]----[%d]:father\n",i,getpid());48       }49     return 0;50 }

结果：