数学实验第三版（主编：李继成赵小艳）课后练习答案（十）（2）（3）

实验十：非线性函数极值求解

练习二

1.求解极值问题:

(1) s.t.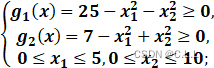

function [c,ceq]=fun(x)
c(1)=-(25-x(1)^2-x(2)^2);
c(2)=-(7-x(1)^2+x(2)^2);
ceq=0;

换一个窗口运行下面的程序：

clc;clear;
f=@(x)-2*x(1)-x(2);
a=[];
b=[];
aeq=[];beq=[];
u=[5;10];
l=[0;0];
x0=[1;0];
[x,min]=fmincon(f,x0,a,b,aeq,beq,l,u,@fun)

x =

4.0000

3.0000

min =

-11.0000

注：创立的fun函数中，第一个返回值为非线性不等式且是小于等于0的，第二个为非线性等式，注意这里的细节。

(2)

function [c,ceq]=fun1(x)
c(1)=1.5+x(1)*x(2)-x(1)-x(2);
c(2)=-x(1)*x(2)+10;
ceq=0;

在另一个窗口运行一下程序：

clc;clear;
f=@(x)exp(x(1)+x(2))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1);
a=[];
b=[];
aeq=[];beq=[];
u=[];
l=[0;0];
x0=[1;0];
[x,min]=fmincon(f,x0,a,b,aeq,beq,l,u,@fun1)

x =

0.9477

10.5523

min =

2.8470e+07

注意：创建函数时名字不要和第一问重复，否则后出错。

练习三

1.求解二次规划问题:

（1）

clc;clear;
h=[0.5,00,0.5];
c=[-1;-2];
a=[2,3;1,4];
b=[6;5];
aeq=[];beq=[];
u=[];
l=[0;0];
[x,min]=quadprog(h,c,a,b,aeq,beq,l,u)

x =

1.2353

0.9412

min =

-2.5147

因为是二次规划问题，h矩阵为正定矩阵，则局部最小值即为全局最小值。

（2）

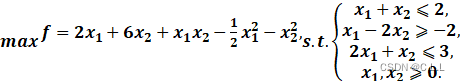
clc;clear;
h=-[-0.5,0.50.5,-1];
c=[2;6];
a=[1,1;-1,2;2,1];
b=[2;2;3];
aeq=[];beq=[];
u=[];
l=[0;0];
[x,min]=quadprog(h,c,a,b,aeq,beq,l,u)

x =

1.0e-11 *

0.0109

0.3751

min =

2.2725e-11

由于算法存在微小误差，经过观察得知，当x1和x2均取0时，有最大值为0；

2.某3只股票49个周末的收盘价如表10.1所示.

表10.1 A、B、C三只股票49个周末的收盘价

周数	A股票	B股票	C股票	周数	A股票	B股票	C股票
1	10.3	0.77	10.6	28	12.4	1.32	15.6
2	10.6	0.81	11.2	29	12.4	1.32	15.5
3	10.8	0.89	11.9	30	12.7	1.29	15.8
4	10.7	0.93	11.7	31	12.5	1.32	15.4
5	10.8	0.90	11.6	32	12.3	1.32	14.9
6	10.8	0.93	11	33	12.6	1.33	15.3
7	11.2	1.01	12.1	34	12.4	1.37	15.6
8	11.3	0.96	13.2	35	12.6	1.48	14.2
9	11	2	12.6	36	12.1	1.49	13.8
10	10.9	1.04	12.6	37	11.9	1.51	14
11	10.6	1.04	12.6	38	11.9	1.32	13.8
12	10.9	1.09	12.6	39	12.4	1.32	14.2
13	11.5	1.1	12.7	40	12.1	1.3	13.8
14	11.5	1.26	13.6	41	12	1.28	14
15	11.8	1.17	14.2	42	12.4	1.17	14.3
16	12.2	1.06	14.7	43	12	1.14	13.6
17	12	1.13	14.4	44	12	1.08	14.1
18	12.1	1.09	14.3	45	12	1.09	14.4
19	12.3	1.03	15	46	12.1	1.07	14.6
20	11.4	1.08	14.9	47	12	1.2	14.4
21	11.4	1.08	13.4	48	12	1.24	14.4
22	11.9	1.12	14	49	12.1	1.26	14.5
23	11.9	1.12	14.4
24	12	1.15	14.7
25	11.8	1.2	14.3
26	11.8	1.2	14.7
27	12.2	1.24	14.9

(1)分别计算这3只股票2-49周的周收益率、平均收益率和周收益率的协方差矩阵;

clc;clear;
x1=[10.3,10.6,10.8,10.7,10.8,10.8,11.2,11.3,11,10.9,10.6,10.9,11.5,11.5,11.8,12.2,12,12.1,12.3,11.4,11.4,11.9,11.9,12,11.8,11.8,12.2,12.4,12.4,12.7,12.5,12.3,12.6,12.4,12.6,12.1,11.9,11.9,12.4,12.1,12,12.4,12,12,12,12.1,12,12,12.1];
x2=[0.77,0.81,0.89,0.93,0.90,0.93,1.01,0.96,2,1.04,1.04,1.09,1.1,1.26,1.17,1.06,1.13,1.9,1.03,1.08,1.08,1.12,1.12,1.15,1.2,1.2,1.24,1.32,1.32,1.29,1.32,1.32,1.33,1.37,1.48,1.49,1.51,1.32,1.32,1.3,1.28,1.17,1.14,1.08,1.09,1.07,1.2,1.24,1.26];
x3=[10.6,11.2,11.9,11.7,11.6,11,12.1,13.2,12.6,12.6,12.6,12.6,12.7,13.6,14.2,14.7,14.4,14.3,15,14.9,13.4,14,14.4,14.7,14.3,14.7,14.9,15.6,15.5,15.8,15.4,14.9,15.3,15.6,14.2,13.8,14,13.8,14.2,13.8,14,14.3,13.6,14.1,14.4,14.6,14.4,14.4,14.5];
m1=[];m2=[];m3=[];
for i=2:49
k1=(x1(i)-x1(i-1))/x1(i-1);
k2=(x2(i)-x2(i-1))/x2(i-1);
k3=(x3(i)-x3(i-1))/x3(i-1);
m1=[m1,k1];
m2=[m2,k2];
m3=[m3,k3];
end
m1,m2,m3
a1=mean(m1),a2=mean(m2),a3=mean(m3)
cov(m1,m2),cov(m1,m3),cov(m2,m3)

m1 =

列 1 至 10

0.0291 0.0189 -0.0093 0.0093 0 0.0370 0.0089 -0.0265 -0.0091 -0.0275

列 11 至 20

0.0283 0.0550 0 0.0261 0.0339 -0.0164 0.0083 0.0165 -0.0732

列 21 至 30

0.0439 0 0.0084 -0.0167 0 0.0339 0.0164 0 0.0242 -0.015

列 31 至 40

-0.0160 0.0244 -0.0159 0.0161 -0.0397 -0.0165 0 0.0420 -0.0242 -0.0083

列 41 至 48

0.0333 -0.0323 0 0 0.0083 -0.0083 0 0.0083

m2 =

列 1 至 10

0.0519 0.0988 0.0449 -0.0323 0.0333 0.0860 -0.0495 1.0833 -0.4800

列 11 至 20

0.0481 0.0092 0.1455 -0.0714 -0.0940 0.0660 0.6814 -0.4579 0.0485

列 21 至 30

0.0370 0 0.0268 0.0435 0 0.0333 0.0645 0 -0.0227 0.0233

列 31 至 40

0 0.0076 0.0301 0.0803 0.0068 0.0134 -0.1258 0 -0.0152 -0.0154

列 41 至 48

-0.0859 -0.0256 -0.0526 0.0093 -0.0183 0.1215 0.0333 0.0161

m3 =

列 1 至 10

0.0566 0.0625 -0.0168 -0.0085 -0.0517 0.1000 0.0909 -0.0455 0 0

列 11 至 20

0 0.0079 0.0709 0.0441 0.0352 -0.0204 -0.0069 0.0490 -0.0067 -0.1007

列 21 至 30

0.0448 0.0286 0.0208 -0.0272 0.0280 0.0136 0.0470 -0.0064 0.0194 -0.0253

列 31 至 40

-0.0325 0.0268 0.0196 -0.0897 -0.0282 0.0145 -0.0143 0.0290 -0.0282 0.0145

列 41 至 48

0.0214 -0.0490 0.0368 0.0213 0.0139 -0.0137 0 0.0069

a1 =

0.0037

a2 =

0.0291

a3 =

0.0073

ans =

0.0006 -0.0007

-0.0007 0.0462

ans =

0.0006 0.0004

0.0004 0.0016

ans =

0.0462 -0.0017

-0.0017 0.0016

注：协方差矩阵中每个数代表的含义为：

以cov(x,y)为例，x的方差，x和y的协方差，y和x的协方差，y的方差。

(2)在允许卖空的条件下,给出这3只股票风险最小的投资策略.

根据以上数据构造数学模型：

d=0.5;
h=[0.0006,-0.0007,0.0004-0.0007,0.0462,-0.00170.0004,-0.0017,0.0016];
c=[];
a=-[0.0037,0.0291,0.0073];
b=[d];
aeq=[1,1,1];
beq=[1];
u=[];
l=[0;0;0];
[x,min]=quadprog(h,c,a,b,aeq,beq,l,u)

x =

0.8106

0.0296

0.1598

min =

2.6477e-04

我们假设投资人想要收益率为50%，那么按照上边的投资方案购买风险最小。

本文由作者自创，由于时间原因，难免出现些许错误，还请大家多多指正。创作不易，请大家多多支持。