源自：自动化学报

作者：张凯, 杨朋澄, 彭开香, 陈志文

“人工智能技术与咨询”   发布

摘 要

传统的多模态过程故障等级评估方法对模态之间的共性特征考虑较少, 导致当被评估模态故障信息不充分时, 评估的准确性较低. 针对此问题, 首先, 提出一种共性–个性深度置信网络 (Common and specific deep belief network, CS-DBN), 该网络充分利用深度置信网络 (Deep belief network, DBN) 的深度分层特征提取能力, 通过度量多模态数据间分布的相似性和差异性, 进一步得到能够反映多模态过程共有信息的共性特征以及反映每个模态独有信息的个性特征; 其次, 基于CS-DBN, 利用多模态过程的已知故障等级数据生成多模态共性–个性特征集, 通过加权逻辑回归构建故障等级评估模型; 最后, 将所提方法应用于带钢热连轧生产过程的故障等级评估中. 应用结果表明, 随着多模态故障等级数据的增加, 所提方法的评估准确率逐渐增加, 当故障信息充足时, 评估准确率可达98.75%; 故障信息不足时, 与传统方法相比, 评估准确率提升近10%.

关键词

多模态过程 / 故障等级评估 / 共性–个性特征 / 深度置信网络 / 带钢热连轧

现代复杂工业过程的大规模连续生产给制造业带来高效益的同时也增大了事故风险. 由于工业过程中的控制回路、过程变量相互耦合, 一个部位的异常变化可能会随着传播不断演变, 微小的故障也可能引起更严重的故障[1]. 因此, 准确判断系统的故障程度并按照故障程度的不同调整生产决策和控制策略, 能够提高生产的高效性和产品质量的稳定性. 目前, 工业过程故障等级评估方法已在有色金属[2]、化工[3]、电力[4]、高铁[5]、船舶[6]等行业成功应用, 并取得良好效果.

随着工业自动化与数据存储技术的快速发展, 基于数据驱动的故障等级评估方法被提出和广泛应用[7-9], 如多元统计分析、机器学习、深度学习等. 常用的多元统计分析方法包括主元分析 (Principal component analysis, PCA)[10]、偏最小二乘 (Partial least squares, PLS)[11]及其拓展方法等, 这些特征提取方法通过将高维数据投影到低维空间来提取关键信息, 并用于进一步的故障评估研究. 随着人工智能的发展, 支持向量机 (Support vector machine, SVM)[12]、判别分析 (Fisher discriminant analysis, FDA)[13]等典型机器学习方法被广泛应用, 这类方法通过建立过程数据与评估指标之间的映射关系来实现故障评估. 其中, SVM通过高维空间映射寻找最优分类超平面, 而FDA通过降维投影建立判别函数. 然而, 这些方法大多局限于浅层学习, 可能无法很好地处理非线性耦合数据, 在故障评估中常与其他特征选择和提取方法相结合. 近年来, 深度学习因其能够自动提取大规模非线性数据的深层特征而被广泛研究与应用, 如卷积神经网络 (Convolutional neural network, CNN)[14]、堆叠自动编码器 (Stacked auto-encoder, SAE)[15] 和深度置信网络 (Deep belief network, DBN)[16]等. 其中, DBN通过数据的概率分布来提取高层表示, 与其他网络相比, DBN兼具生成模型和判别模型双重属性, 具有模型结构简单、训练难度小、易于拓展等优点. 目前, DBN已在图像处理、语音识别、医学诊断等任务中得到了广泛的关注和研究[17].

上述特征提取方法侧重于建立单模态的故障评估模型. 然而, 实际过程中往往存在多种工作模态, 操作条件的变化、产品规格的多样性等使工业过程运行工况复杂多变, 传统的单模态故障等级评估方法难以有效地提取和分析潜在的多模态数据特征, 需要构建适用于多模态过程的特征提取模型和评估指标. 一类常见的方法是将PCA、PLS等基于多元统计的方法扩展至多模态. 例如, 文献[18] 利用多空间PCA获取不同模态的独立特征, 根据投影位置来评估在线过程运行状态, 并综合经济指标来划分性能等级. 文献[19] 采用最小体积椭圆自适应地对各模态特征方差的子空间进行建模, 并根据子空间之间的距离设计评估退化指标. 文献[20] 将经济指标信息融入到慢特征分析中, 协同感知复杂工业过程的静–动态特性变化, 实现了对运行状态的综合评价. 为了提高对具有非线性、动态性多模态过程的处理能力, 一些基于概率的评估框架被提出, 如贝叶斯网络 (Bayesian network, BN)[21]、高斯混合模型 (Gaussian mixture model, GMM)[22]等. 尽管上述方法在一定程度上解决了非线性问题, 但每个模态中仍存在线性假设, 影响了评估的准确性. 当面对复杂的非线性和高维变量时, 深度学习表现出更好的潜力, 基于深度学习的评估模型受到越来越多的研究. 文献[23] 提出了基于条件生成对抗网络的多模态图像质量评估方法, 以平均意见分数建立评估指标, 通过双通道自编码器 (Autoencoder, AE) 提取两个模态不同深度的特征, 并在注意力机制的监督下进行分层融合特征. 文献[24] 针对多模态过程建立多个AE模型, 并将数据压缩到一个共同的更小的潜在空间后进行跨模态重构, 充分利用了故障信息. 文献[25]提出一种基于DBN的主动迁移学习方法, 通过DBN挖掘输入特征与暂态评估结果之间的非线性映射关系, 并结合主动迁移方法提高了在线应用的快速性和鲁棒性.

现有的多模态过程故障等级评估方法针对不同的运行模态分别建立评估模型, 仅考虑在所有模态的故障等级数据均已知条件下如何通过优化学习网络来提高评估的准确率, 未考虑在某些运行模态各种故障等级信息未知下如何改进和优化算法. 并且大部分方法只关注各模态数据的独有特征, 缺少对各模态间共性特征的建模与分析. 实际上, 尽管模态在进行切换, 但并不是所有变量的相关性都随模态切换发生改变, 一些多模态过程具有明显的共同信息. 例如, 在带钢热连轧过程生产不同规格板带时, 上游机架轧制力和辊缝变量遵循相似的轨迹, 而弯辊力变量往往表现出不同的特性. 因此, 分别提取多模态过程的共性特征和各运行模态的个性特征[26], 并根据故障对共性特征和个性特征的影响构建评估模型, 可通过共性特征实现对部分模态缺失信息的补充, 提高多模态过程故障评估的准确性. 本文的故障等级评估方法示意图如图1所示.

※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※

图 1  融合共性–个性特征的故障评估方法示意图

针对多模态过程的故障等级评估问题, 本文以DBN为特征提取基础模型并进行深层次拓展, 提出了一种基于共性–个性深度置信网络 (Common and specific deep belief network, CS-DBN) 的故障等级评估方法. 首先, 针对多模态过程数据, 构建一种CS-DBN模型来提取模态间的共性特征和个性特征; 其次, 提出融合共性–个性特征的故障等级评估方法, 考虑到两种特征对每个等级指标的重要性不同, 给共性–个性特征分配不同的权重因子; 最后, 将所提方法应用到带钢热连轧过程中, 利用实际过程数据验证所提方法的有效性.

1.   问题提出与基本思路

本节以热连轧过程故障等级评估为例, 介绍问题的提出与基本思路. 图2 展示了3种规格带钢生产过程中第2机架轧制力的采样数据, 若把3种规格带钢生产过程视为3种运行模态, 可以看出, 3种模态的轧制力数据具有共性, 即开始轧制阶段呈现上升趋势. 另外, 它们还有各自的独有特征, 如模态3轧制力增长到一定程度就趋于稳定, 而另外两个模态轧制力分别呈现持续增长和持续下降的特征. 传统故障等级评估方法大多根据故障的大小判断故障等级, 忽视了故障对变量变化趋势等深层次特征的影响, 因此容易出现误评估情况. 以轧制力故障为例, 该种故障在热连轧过程中属于较为严重的故障, 3种模态的轧制力故障下的轧制力数据如图3所示. 若已知模态1和模态3的轧制力故障数据, 利用训练好的评估模型评估模态2的故障等级, 如图3所示, 由于模态1和模态3所训练的评估模型并不能完全覆盖到模态2故障数据的全部信息, 因此传统方法容易将该故障错评为一般故障或者正常. 若利用模态2的故障数据提取共性特征, 如图3所示, 该故障对共性特征的影响较大, 利用模态1和模态3共性特征训练好的评估模型可将此故障正确地评估为严重故障. 弯辊力故障也是热连轧过程经常发生的故障, 当弯辊力发生异常后, 会间接影响轧制力的动态设定, 该故障对带钢产品的厚度影响较小, 常被当做轻微的故障. 图4 给出了3种模态弯辊力故障下的数据曲线, 如果利用模态1和模态2的故障数据训练评估模型并评估模态3的故障等级, 由于模态3的故障数据范围已经超越了模态1和模态2的故障数据范围, 传统的评估方法易将该故障误评为严重故障. 而如果利用模态3故障数据提取的共性特征来评估, 如图4所示, 由于共性特征并没有受到较大影响, 因此可被正确评估为轻微故障. 因此, 可以看出, 若不考虑各模态间的共性特征和个性特征, 很容易导致错误的评估结果.

※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※

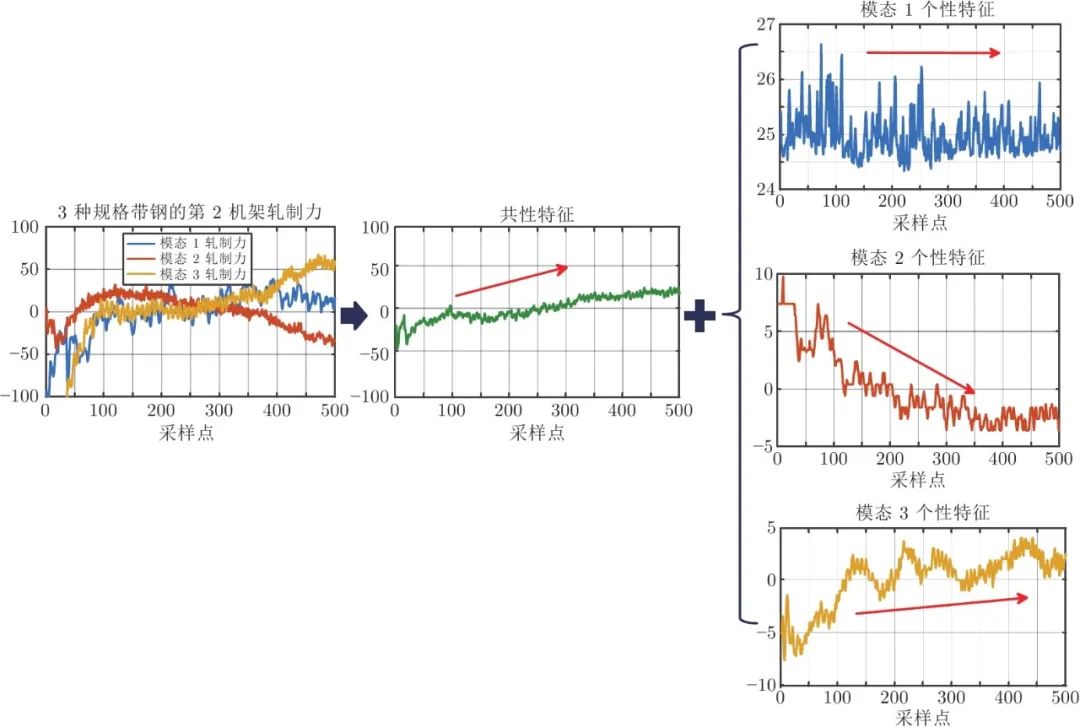
图 2  热连轧过程单变量共性−个性特征分解示意图

※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※

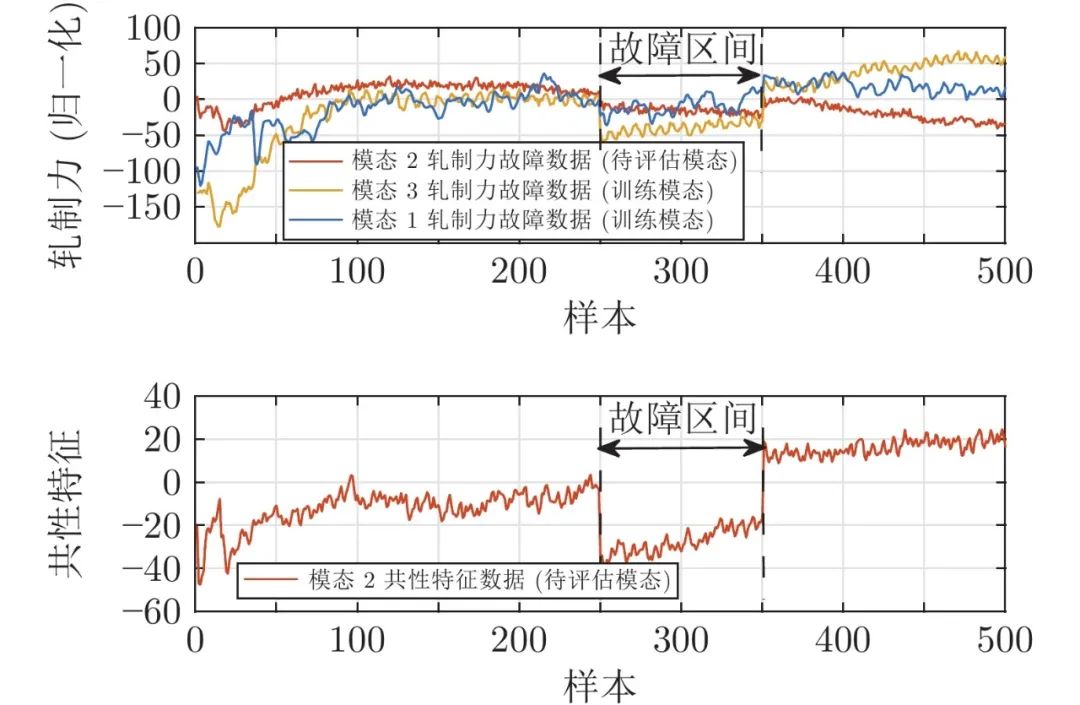
图 3  轧制力故障共性特征等级评估示意图

※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※

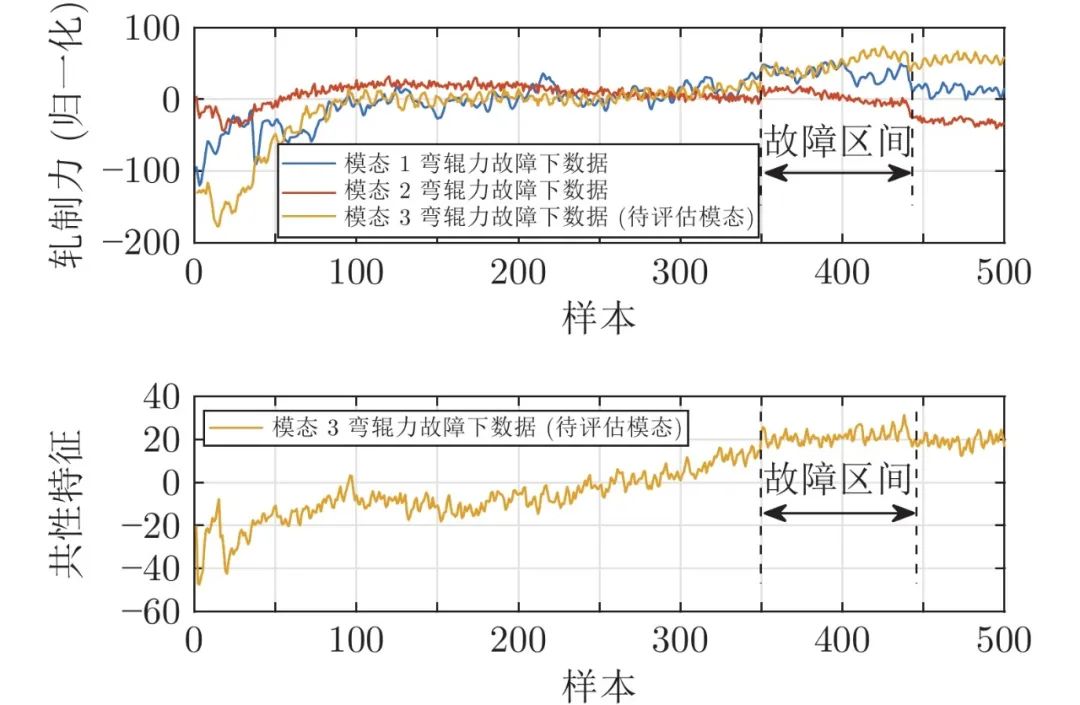
图 4  弯辊力故障共性特征等级评估示意图

实际热连轧生产过程中变量众多且相互耦合关联, 多模态特性也使得过程固有的非线性更加明显. 假设带钢热连轧过程在M 种模态下运行, 每种模态下的过程数据可表示为

 其表示由n 个过程变量Nm 个样本组成的数据矩阵. 如何基于Xm 构建提取各模态的共性特征和个性特征的模型, 对多模态过程故障等级的评估起着关键作用. 为实现这一目的, 较为直接的方法是在传统特征提取的基础上, 深度挖掘各模态特征间的共性和个性部分. DBN作为特征提取方法可实现高维非线性数据的处理. 按照以上思路, DBN可从Xm 中提取到各模态基本特征

为深层特征的维度. 在此基础上, 如何构建从

到共性特征

和个性特

间的映射关系亟待解决, 其中, nc  和ns 分别代表共性特征和个性特征的维度. 不失一般性, 这种映射关系可以定义如下

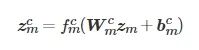
   (1)    

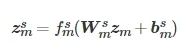
   (2)    

式中, 

分别表示共性特征和个性特征的映射权重, 

分别表示两种特征的偏置,

分别表示两种特征映射的非线性函数.

基于以上思路, 剩余部分的具体工作包括: 第一, 构建共性–个性深度置信网络模型, 实现式 (1) 和式 (2) 所描述的映射关系; 第二, 提出融合共性–个性特征进行故障等级评估的方法.

2.   共性–个性深度置信网络

本节提出了CS-DBN模型来提取各模态数据中隐含的共性特征和个性特征, 同时结合已有方法总结了CS-DBN的特点.

2.1    特征提取网络结构

多模态共性–个性特征提取框架如图5所示. 网络由三部分组成, 分别是预训练网络、特征变换网络和重构网络. 预训练网络建立并行DBN, 以标准化后的模态数据Xm  作为各子网络输入, 提取各模态数据的深层特征Zm . 特征变换网络将每种模态的特征分别分解为共性特征和个性特征, 以预训练网络的输出Zm 作为输入, 结合MK-MMD (Multi-kernel maximum mean discrepancy)[27], 将每个模态特征数据映射为具有最小分布距离的共性特征和具有最大分布距离的个性特征. 同时, 为了增强模型的鲁棒性, 首先, 将获得的各模态共性特征和个性特征通过多层感知机 (Multilayer, perceptron, MLP)[25]层映射至共同的ζ维度; 然后, 将第m个模态学习得到的共性–个性特征与其他模态的共性特征进行加性融合, 以从其他模态学习到的共性特征来增强该模态共性信息的表示, 进而作为重构网络的输入. 重构网络利用权重矩阵的转置重构输入数据得到

, 通常采用反向传播 (Back propagation, BP) 算法, 使用重构数据与原始数据的误差平方和进行反向调参, 以无监督的方式对整个网络进行参数的全局优化.

※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※

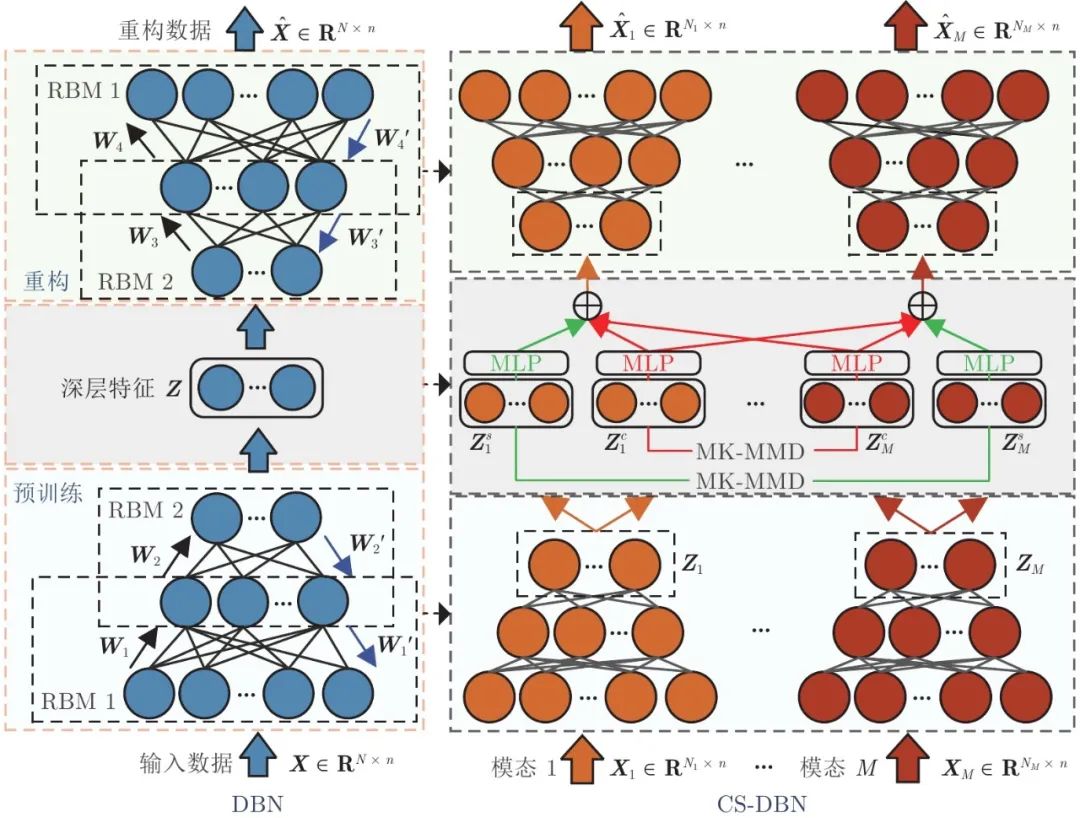
图 5  DBN与CS-DBN网络结构示意图

2.2   DBN预训练

图5 展示了通过DBN逐层预训练提取每个模态运行数据特征的过程. DBN由多个受限玻尔兹曼机 (Restricted Boltzman machine, RBM) 堆叠而成, RBM由可见层和隐藏层组成, 将前一个RBM的隐藏层输出作为下一个RBM可见层的输入, 自下而上初始化DBN的参数. 在训练过程中, 单个RBM采用对比散度 (Contrastive divergence, CD)[28]算法进行一步吉布斯采样, 参数更新公式为

   (3)    

   (4)    

   (5)    

式中, vi 和ai 分别表示第i 个可见单元的状态和偏置, hj  和bj 分别表示第j 个隐藏单元的状态和偏置,

为显层和隐层通过条件概率采样生成的重构数据; 

为第i 个可见单元及第j 个隐藏单元间的连接权重; ε  为学习率. 此外, 为了提高训练的速度, 避免过拟合, 本文将

的更新规则分别改进为

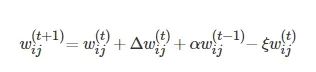
   (6)    

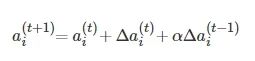
   (7)    

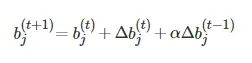
   (8)    

式中, α 为加速学习过程的动量, t 表示迭代的次数, ξ 为权重衰减项. 通过这种方式逐个训练RBM. 在提出的模型中, 第一层的可见单元是实值, 使用高斯受限玻尔兹曼机来训练网络的第一层[29], 然后使用伯努利受限玻尔兹曼机进行深层RBM的训练.

DBN预训练可称为编码过程, 第m 个模态的数据

经过DBN预训练后, 最高层RBM的输出为深度特征Zm . 再将深度特征数据反向逐层解码, 增加与DBN对应的后向微调步骤, 可以得到微调后的重构数据

. 每个模态无监督的DBN重构训练损失函数为

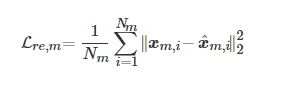
   (9)    

2.3   特征转换层

在提取的多模态深度特征基础上, 进一步设计特征转换层. 预训练后, 将各模态深层特征

维共性特征空间和ns 维个性特征空间, 并将共性–个性特征视为来自两个分布的样本, 采用MK-MMD计算分布距离来分离两种特征.

MMD通过核映射方法将两个分布的关键统计特征嵌入到高维再生希尔伯特空间 (Reproducing kernel Hilbert space, RKHS) 中, 然后计算核均值嵌入之间的距离, 但MMD在很大程度上依赖于核函数的选择. 为了解决核函数对最终映射性能的影响, 本文采用MK-MMD算法, 该算法在原始MMD特征核的基础上, 利用多个高斯核的线性组合来增强距离度量性能, 从而能够更准确地将输入空间的值映射到RKHS中得到最优值.

设m1 和 m2 分别代表 M 个模态中任意两个模态, 第m1个模态的共性特征数据

满足分布 p , 第 m2 个模态的共性特征数据

 满足分布q, m1,m2=1,2,3,⋯,M, 则由MK-MMD定义的p 与q 之间距离的经验估计为

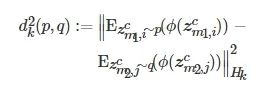
   (10)    

式中, Hk [27]是具有特征核k 的RKHS, E(⋅) 表示给定分布的期望, ϕ(⋅) 表示原始特征空间映射到RKHS的映射函数, 与特征映射关联的特征内核

, MK-MMD使用多个核的凸组合, 表示如下

   (11)    

其中, 系数βu 被约束以保证导出的多核k 特性, d 为特征核的个数,

可表示如下

   (12)    

式中, σu 为核函数的带宽.

在训练阶段, 为了降低计算复杂度, 本文采用Gretton等[27]提出的MK-MMD的无偏估计. MK-MMD的计算可以转换为

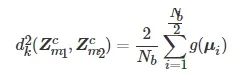
   (13)    

其中, 四元组

定义为 

为一个批次的样本数. 

可计算为

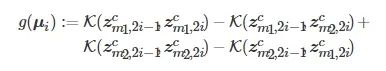
   (14)    

同样, 类似于式 (13), 可以计算两两模态个性特征之间的MK-MMD距离

. 在本文框架中, 不同模态共性特征

应有尽可能相似的分布, 同时模态个性特征

的分布尽可能差异较大. 因此, 需要最小化

. 将距离度量加入网络的损失函数中, 模态共性特征和个性特征的梯度从两个不同的来源计算: 各子网络重构误差和两两模态间不同分布的MK-MMD距离. 并通过BP算法反向调节各部分参数. 整体损失函数为

   (15)    

其中,

分别为重构部分以及共性–个性特征部分的参数, 用以平衡各项, 使网络损失函数最小化.

2.4   方法特点及对比分析

在构建的CS-DBN网络中, 共性特征的维度nc 需要在模型训练的时候确定. 根据式 (14) 可以看出, 当nc 从1开始逐渐增大时, 各模态共性特征间的MK-MMD距离不会有较大增加. 由于整体的重构误差

逐渐减小, 因此

会呈现下降趋势. 当nc取值增大时, 共性特征间的距离会逐渐变大, 导致

的下降变得不明显. 综上, 在训练过程中可以将nc从1逐渐增大到

, 并记录损失函数值

, 当损失函数值不再明显减小时, 记录此时的nc.

CS-DBN通过概率生成和非线性映射建立原始数据与特征间的关系, 更适合于复杂非线性工业过程. 与文献[30] 和文献[31] 中方法相比, 在特征提取的原理方面, CS-DBN在满足共性特征距离最小、个性特征距离最大的前提下, 通过最小化重构误差来获取特征, 充分地结合了传统方法的特点. 在训练过程中, CS-DBN不要求各模态的数据等长, 这也极大地扩展了方法的通用性. 从投影空间的角度获取的共性特征和个性特征相互正交, 这有利于构建互补的故障检测指标, 而CS-DBN和基于张量分解方法不能满足特征的正交性, 各种方法的特点及比较总结如表1所示. 接下来, 将介绍如何结合CS-DBN的特点构建故障等级评估方法.

※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※

表 1  各类共性–个性特征提取方法特点总结

3.   融合共性–个性特征的故障等级评估

本节在CS-DBN的基础上, 提出了融合共性–个性特征进行故障等级评估的方法.

3.1   故障等级划分

如第1节所描述, 模态间的共性特征关联了多个操作模态的状态, 影响共性特征的故障会引起系统结构性故障, 表现为影响多个模态的关键质量指标, 属于严重故障. 影响模态个性特征的故障, 可以通过系统的闭环调节及时补偿, 不会对关键指标产生影响. 并且, 由于特征变量间的耦合作用, 影响各模态个性特征的故障可能会由于未及时检修或故障较大等原因, 演变为影响多模态共性特征的故障. 因此, 可以根据故障对共性特征和个性特征的影响构建评估方法. 本文结合国家标准GB/T709-2006将故障划分为3个等级: “轻微故障”、“一般故障”、“严重故障”. 具体来说, 当有故障发生时, 将主要影响个性特征且不影响质量指标的故障划分为“轻微故障”; 将同时影响共性特征和个性特征且对质量指标的影响较小的故障划分为“一般故障”; 将对共性特征影响较大且对质量指标影响较大的故障划分为“严重故障”.

3.2   故障等级评估模型

基于CS-DBN模型, 并利用第3.1节已知的各模态故障等级数据, 可获得多模态共性特征集

, 包含正常数据的共性特征

和故障数据的共性特征

, 同时获得多模态个性特征集Zsm, 包含正常数据的个性特征

和故障数据的个性特征

. 将每个模态特征数据样本与故障等级标签进行模式匹配可得到数据

 和

 其中

为样本对应的G 个故障等级标签. 通过逻辑回归(Logistic regression, LR)[32]的多分类“一对多”策略, 将多个二分类进行独立调优并整合. Softmax函数是LR在多分类的推广, 其输出为样本点属于每一类的概率, 共性特征中第i 个样本

属于每个等级的概率可计算为

   (16)    

式中, 

为权重矩阵. 类似地, 个性特征属于每一类的概率

也可以按照式 (16) 计算得到.

共性特征和个性特征共同决定了故障等级且对每个等级的故障贡献值不同, 因此不能仅将两种特征通过拼接或加和来进行等级评估训练. 为了获得更好的性能, 在训练阶段根据两种特征的重要性进行加权, 得到属于每个等级的概率

, 最终

属于每个等级的概率

计算为

   (17)    

最终的评估结果Grade(xm,i) 确定为

中概率最大值对应的等级. 式(17)中, λ(0≤λ≤1) 为特征的加权系数, λ 越大表示共性特征分量在等级评估过程中所占比重越大. 当λ=0 时, 表示只有个性特征分量, 个性特征反映了各个模态内的信息, 因此, 当用于训练模型的各模态故障信息不足时, 可能会影响评估精度. 当λ 逐渐增大至1时, 表示在确定故障等级时只有共性特征分量起作用.

3.3   基于CS-DBN的故障等级评估方法总结

以热连轧过程为例, 本文所提出的方法可总结如图6所示. 选取该过程几个典型规格的带钢轧制过程作为M 个工作模态, 并将这些模态的运行数据导出作为CS-DBN的网络训练数据. 同时, 可以利用各模态已知的故障等级数据生成共性–个性特征正常/故障特征集, 用来训练评估模型. 当在线得到待评估模态数据后, 可利用训练的模型参数进行在线故障等级评估. 详细的方法总结可描述如下:

※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※

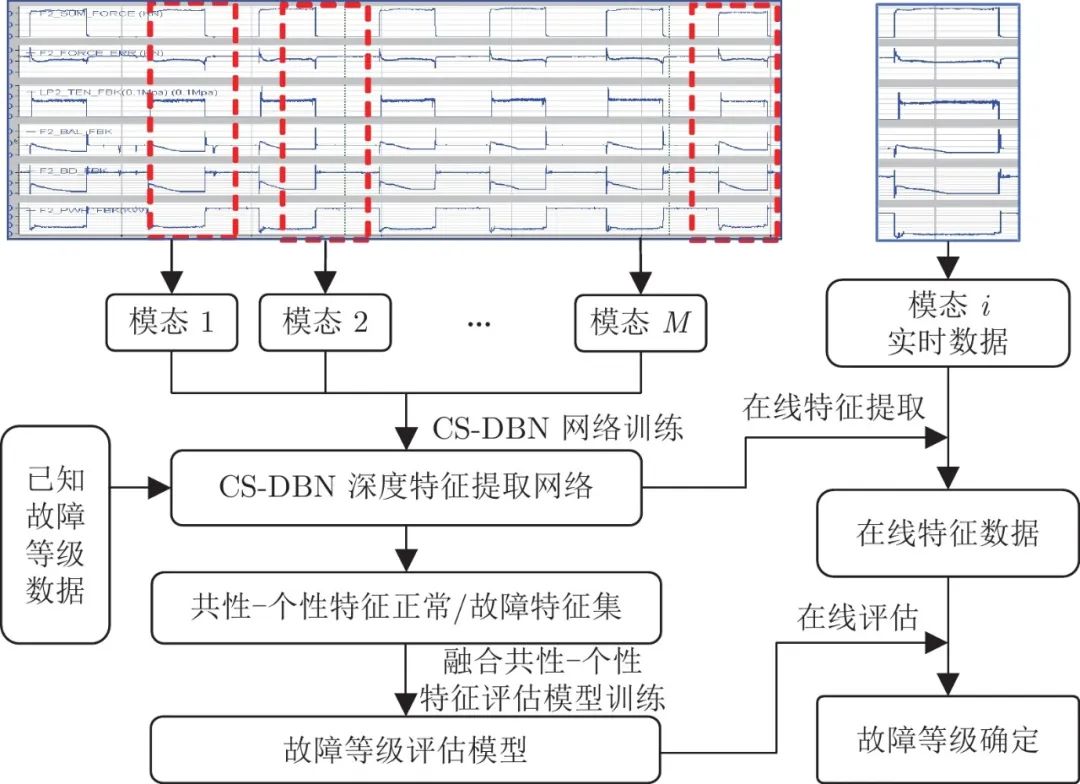
图 6  基于CS-DBN的故障等级评估流程图

1) 离线建模:

a) CS-DBN模型的构建:

• i) 获取M 个模态正常工况下的数据并进行Z-Score标准化处理;

• ii) 建立M 个DBN子网络, 通过式 (6) ~ (8) 更新参数至顶层RBM完成预训练;

• iii) 随机初始化共性–个性特征映射权重

  

  ;

• iv) 通过式 (13) 分别计算各模态共性特征分布距离

  

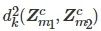
  及个性特征分布距离 

  

  ;

• v) 将共性–个性特征融合进行重构训练, 通过梯度下降反向微调各层网络以及

  

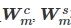
  相关参数, 训练CS-DBN模型至式 (15) 收敛.

b) 等级评估模型的构建:

• i) 获取M 个模态已知的故障等级数据, 通过训练完成的CS-DBN模型提取每个模态正常数据和故障数据的共性特征

  

  ;

• ii) 对已知故障进行等级划分, 将共性–个性特征与等级标签进行匹配得到数据

  

  

  ;

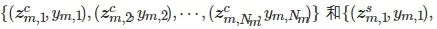
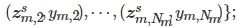
• iii) 训练加权LR的各等级参数

  

  , 根据式 (17) 确定故障等级.

2) 在线应用:

a) 获取待评估模态数据

并进行标准化处理;

b) 通过CS-DBN模型得到在线数据共性–个性特征

;

c) 基于

, 通过式 (17) 确定故障等级.

4.   带钢热连轧过程应用验证

本节将所提方法用到热连轧精轧过程中, 通过实际精轧过程数据验证本文方法的评估效果.

4.1   过程描述及数据描述

 4.1.1    过程描述

带钢热连轧主要由加热炉、粗轧机、飞剪、精轧机组、层流冷却和卷取机等相互耦合的工序构成, 热连轧过程布局如图7所示. 其中, 精轧机组是控制成品质量和保障系统安全的关键环节, 精轧机组由F1 至F7 共7台机架串联组成, 每个机架由一对工作辊、一对支撑辊以及相应的液压压下装置等部分构成. 四辊轧机的下支撑辊的下部设有轧制力检测传感器. 工作辊之间的辊缝控制由高精度的液压伺服控制系统完成, 通过设定辊缝值来保证带钢的出口厚度. 出口厚度是关键性能指标之一, 厚度精度取决于精轧机压下系统和厚度控制系统 (Automatic gauge control, AGC) 的设备形式, 现代化AGC能综合采用多种形式的厚度自动控制系统, 以适应不同钢种、规格和工艺参数变化的要求.

※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※

图 7  热连轧机组及精轧机组布局图

 4.1.2    数据描述

本文采用某钢铁厂带钢热连轧现场采集的过程数据来验证所提方法的有效性. 数据描述如表2所示. 选择Q235B碳素结构钢4种规格带钢的生产过程作为4种模态, 4种规格带钢的出口厚度分别为2.30 mm、2.70 mm、3.00 mm和3.95 mm. 评估数据为该过程的关键过程变量, 包括7个机架的辊缝、轧制力和弯辊力 (第1机架无弯辊力控制) 共20个过程变量.

※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※

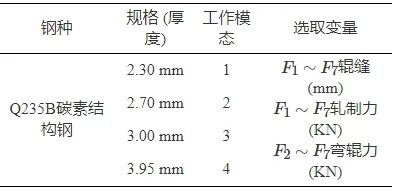
表 2  热连轧过程多模态数据描述

不同模态的故障等级数据可通过如图8所示的热连轧过程故障注入系统获得. 该系统集成了热连轧过程压下、温降、弯辊、活套等各类机理模型, 通过读取实际的多规格生产过程、工艺设定及轧机的状态数据, 并利用增量叠加形式将各类故障注入到正常的过程数据, 从而获得各种等级的故障数据. 实验表明, 该系统可较好地模拟实际生产过程的故障产生、传播及对产品质量的影响. 在该系统中可读取表2所描述的4种规格的正常过程数据, 并通过选择故障类型、故障大小及故障发生位置等信息实现故障注入.

※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※

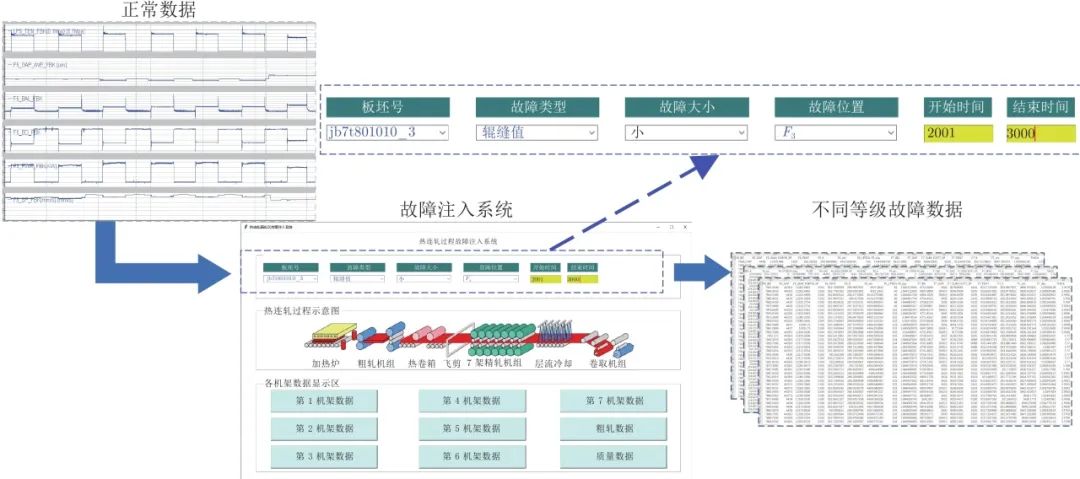
图 8  热连轧故障注入系统

本文选取了热连轧过程常见的3类典型故障进行方法验证. 3类故障按照第3.1节的划分标准可分别归类为“轻微故障”、“一般故障”和“严重故障”. 故障类型1为F5弯辊力传感器故障, 由于系统的闭环控制, 该故障可以通过增大F6和F7的弯辊力来补偿, 因此只影响各模态的个性特征, 不会对出口厚度造成影响. 故障类型2为F4辊缝故障, 该故障将影响F4和F5的轧制力和辊缝, 但由于AGC系统的补偿控制, 可以通过压下设备做相应调节来消除厚度偏差. 故障类型3为F2与F3间冷却水阀执行器故障, 该故障会导致F3轧钢入口温度升高, 由于前馈控制器的影响, F3及之后机架的轧制力和辊缝都会受到影响, 最终影响钢品出口厚度, 在这种情况下, 任何带钢类型的生产过程都将受到影响, 因此系统的共性特征和个性特征都将受到影响. 综合考虑故障影响的变量以及钢品出口厚度差, 本文将每个模态的数据划分4个等级, 故障划分结果如表3所示.

※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※

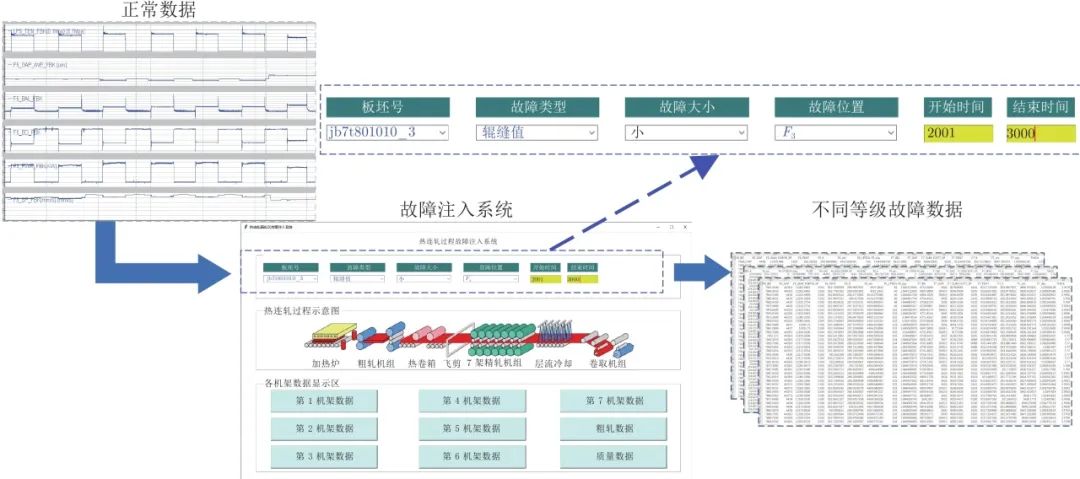
表 3  热连轧过程故障等级划分及标签添加

4.2   故障信息已知下的等级评估

 4.2.1    模型训练

如第3.3节所描述, 整个模型训练分为两步: 1) CS-DBN特征提取模型; 2) 故障等级评估模型. 选择第4.1.2节中描述的4个模态的正常工况数据训练CS-DBN模型, 每个模态数据包含20个变量3000个样本, 组成训练集

.

CS-DBN的训练过程首先对每个模态建立DBN子模型. 采用试错法进行超参数选择, 逐层设置隐含层节点数并依次叠加RBM层数, 根据损失曲线收敛的速度和大小初步确定DBN的结构参数、损失函数L的各约束项以及迭代步数 (epoch). 中间特征转换层共性–个性特征维度nc和ns是影响评估结果的关键参数, 维度较低可能不能充分提取信息, 维度较高则会产生冗余信息. 在确定维度值时, 首先固定nc为1, ns由1逐渐增大, 观察收敛曲线, 可确定获得最小收敛值时ns维度为7; 再固定ns值, 逐渐增加共性特征维度, 不同nc值的重构误差收敛值如图9所示. 为了简化模型结构, 最终选择最佳共性特征维度为5. 综合以上调试结果, DBN结构最终包含2个隐含层, 预训练部分最佳DBN网络结构为20-35-14, 中间特征转换层权重设置为

. 批次数Nb 设置为80, 学习率ε 为0.0001, 迭代步数设置为600次, 随机失活率dr设置为0.5, 具体模型参数设置如表4所示.

※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※

图 9  共性特征维度nc与重构误差

※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※

表 4  CS-DBN模型参数

为验证本文所提方法的收敛效果, 图10给出了CS-DBN训练过程中的迭代曲线. 其中, 图10(a)为CS-DBN损失函数L 在训练过程中的迭代曲线. 可以看到, 在迭代次数达到400步时, 训练过程迭代曲线已经明显收敛. 图10(b)、图10(c)为不同模态的共性特征间和个性特征间MK-MMD值的迭代曲线. 可以看出, 随着训练次数的增加, 不同模态的共性特征间MK-MMD值呈现出不断减小的趋势至收敛, 反之个性特征间MK-MMD值随迭代次数逐渐增大. 这反映出MK-MMD方法可以区分不同模态数据分布间的相似性和差异性.

※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※

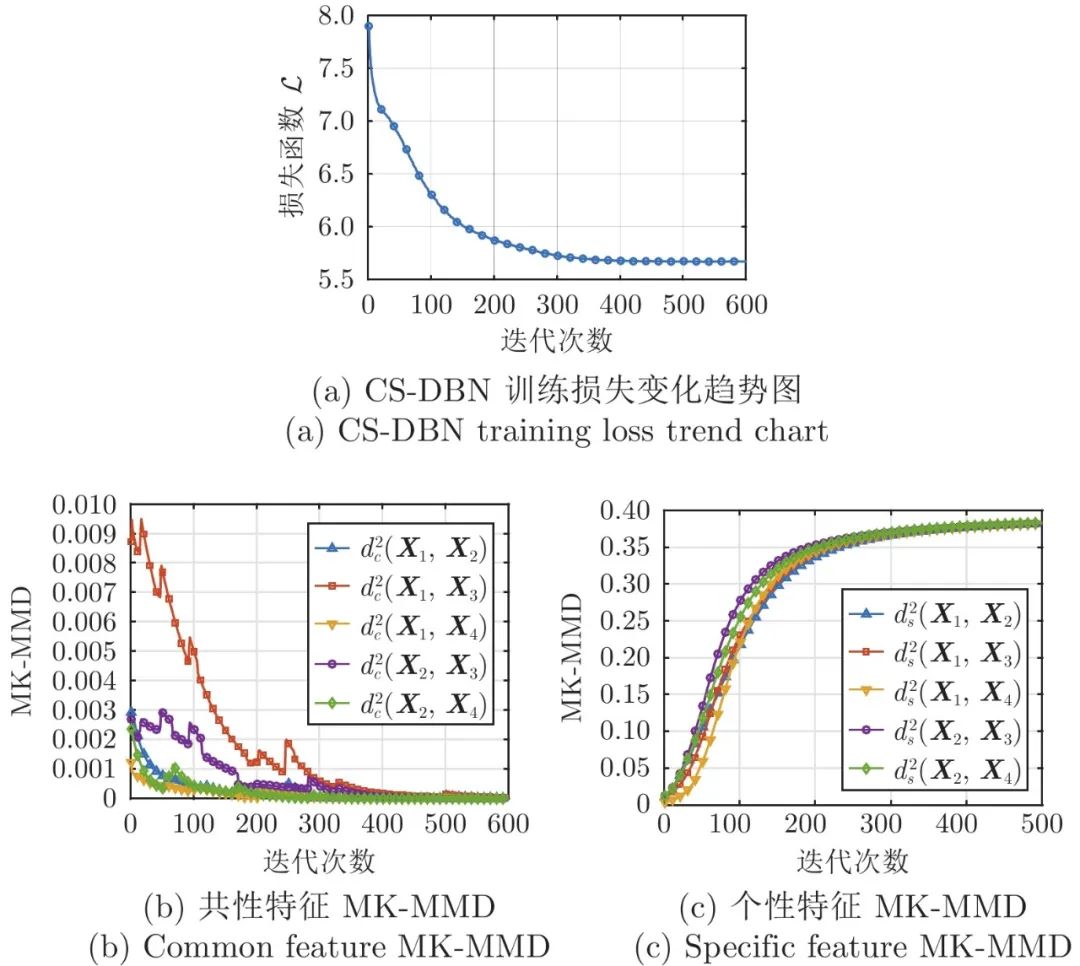
图 10  CS-DBN训练过程迭代曲线

基于CS-DBN模型, 可获得各模态正常工况数据和不同等级故障数据的共性特征

, 

以及个性特征

, 

. 共性–个性特征与等级标签匹配后用于训练等级评估模型部分. 等级评估模型训练集由每种模态正常数据以及不同等级故障数据各2000组组成. 测试集为第4个模态的数据, 包括1000组正常数据和3000组各等级故障数据.

 4.2.2   等级评估结果

为了验证所提方法的应用效果, 本文将基于CS-DBN的等级评估结果与SVM、FDA两类典型机器学习方法以及DBN、SAE结合Softmax深度学习方法的等级评估结果对比, 以说明本文所提方法的优越性. 4种对比方法对模态数据进行整体建模, 利用4个模态的正常数据和已有的各模态等级故障数据训练评估模型. 其中, SAE的隐层神经元数设置为40-25-4, DBN结合Softmax的网络结构设置为35-14-4, SVM的核函数设置为径向基核函数. 为了清晰地展示评估精度, 本文引入准确率(Accuracy)、精确率(Precision)、MacroF1作为评估指标[15, 25].

当训练过程4个模态全部故障信息已知时, 等级评估结果如表5所示. 对比可知, 在4个模态各等级故障信息已知的情况下, 5种方法评估结果都有较高的准确率、精确率和MacroF1. 其中, 融合共性–个性的故障等级评估方法的各项指标均达到98% 以上, 高于其他4种方法. 因此, 融合多模态共性–个性特征的评估方法可以更加有效准确地判断故障等级.

※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※

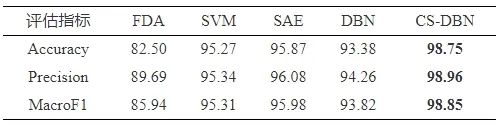
表 5  各模态全部故障信息已知下的评估结果 (%)

4.3   故障信息部分已知的等级评估

为了进一步验证本文方法在多模态故障数据不充分下的应用效果, 本节考虑训练过程中多模态部分故障信息不全的情况, 设计包含不同故障信息的案例, 并通过新模态数据进行评估结果验证.

4.3.1   故障信息不完全情况下的评估结果

在CS-DBN模型训练完成后, 选择4个模态的正常数据以及前3个模态的部分故障数据作为评估模型的训练集. 同时将第4个模态的各等级数据共4000组作为测试集, 即在训练过程中测试集的各等级故障数据均未参与故障等级评估模型的训练.

表6以准确率指标为例展示了各模态不同故障组合案例下的评估结果. 案例A考虑了每个训练模态中包含最多两种等级故障数据下的评估准确率, 其中A-1到A-8是各模态间不同的组合情况. 可以看出, 当故障信息较少时, CS-DBN方法整体故障等级评估准确率在60.00% 以上, 均高于其他4种方法, 同时, 在多数情况下, SVM和FDA方法评估失败(Accuracy ≤≤ 50.00%). 案例B设置为每个模态均有两种等级的故障数据, 故障信息较案例A增多. 从评估结果可以看出, 与案例A相比, 在B-1至B-8不同故障数据组合情况下所有方法的评估准确率均有所提升, CS-DBN在某些故障组合下准确率可达到85.50%, 平均准确率为71.92%, 远高于DBN的61.47% 和SAE的58.25%. 在案例C中, 某些模态的故障等级数据从两种增加至三种, 更多的故障数据参与训练提升了评估效果. 其中CS-DBN方法在所有故障组合下准确率均高于70.00%, 平均准确率为73.12%, 高于DBN的70.47% 和SAE的64.85%. 同时, FDA和SVM方法也均超过50.00%. 案例D设置为训练过程中至少有两个模态有三种等级的故障数据. 评估结果显示, CS-DBN方法的平均准确率为80.79%, 同时在4个故障组合中, 准确率均高于80.00%, 最高为88.25%. 与之相比, FDA和SVM平均值仍为50.00% 左右, DBN和SAE方法也无较大提升.

※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※ ※

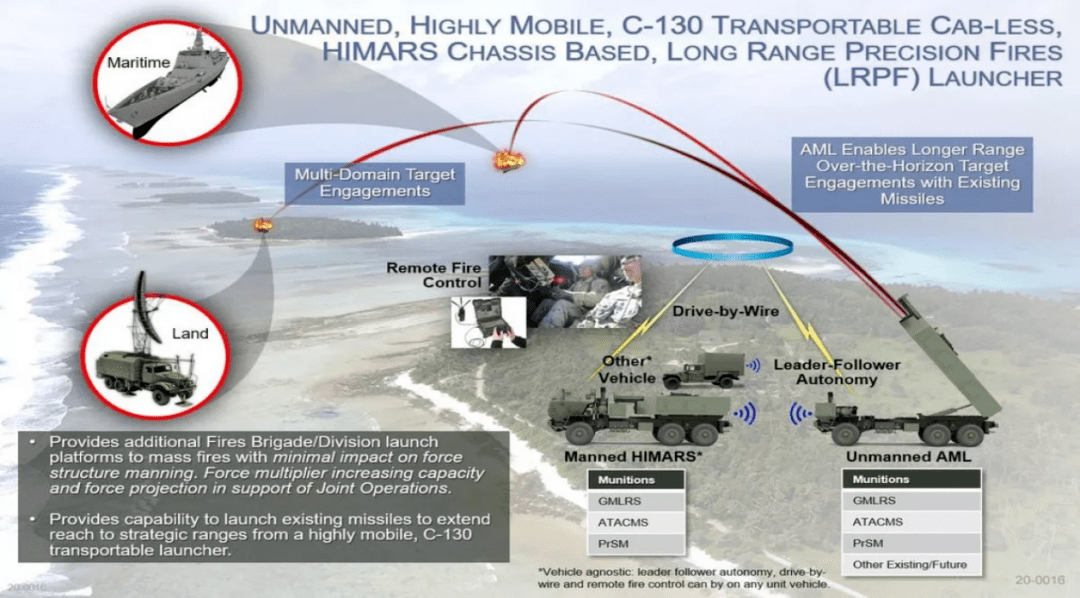
表 6  各模态部分故障信息已知下的评估准确率结果 (%)

总结表6可知, 随着更多的故障等级数据参与训练, 5种方法的评估准确性都有所增加. CS-DBN方法因其可以提取多模态过程的共性信息, 能够更好地学习到多模态过程同一等级故障数据间的共性特征, 与传统方法相比, 评估准确率提升近10%. 本文所提模型可以更准确地评估未知故障信息下的模态所发生的故障.

 4.3.2   待评估模态故障信息未知下的评估结果

当前3个模态的全部故障信息已知时, 选择4个模态的正常数据以及前3个模态的各等级故障数据训练评估模型, 使用第4个模态的各等级数据(均1000组) 进行测试. 图11(a) ~ 图11(e)分别展示所提方法和对比方法的等级评估结果. 如图11(b)和图11(c)所示, DBN和SAE在“严重故障”和“一般故障”等级中有较多的误评估样本. 由图11(d)和图11(e)可以看出, 当待评估模态故障信息未知时, SVM和FDA的评估精度较低, 其中FDA未能区分“严重故障”和“一般故障”, 造成了精确率和MacroF1值失效. CS-DBN方法的评估准确率达到了92.40%, 精确率达到了92.64%, MacroF1达到了92.37%, 仅在“正常数据”和“轻微故障”里有少量评估失误, 评估准确率较第4.3.1节中案例D的结果提升了11.61%. 可以看出, 当用于训练的故障信息增多时, 本文所提方法能够充分利用不同模态的共性–个性特征, 进一步提高模型的性能.

图 11  前3个模态全部故障信息已知时的评估结果

 4.3.3    权重因子λ对评估结果的影响分析

图12 展示了在不同故障信息的实验中权重系数取值与评估准确率的关系. 图12 中, 实验1至实验10为评估模型训练中故障信息逐渐增多的代表性案例. 例如, 实验1中故障信息为模态1至模态3分别含有一种故障等级数据; 实验5中故障信息包括模态1的“轻微故障”、模态2的“一般故障”与“严重故障”、模态3的“轻微故障”与“一般故障”; 实验10包含4个模态的全部故障信息数据. 当λ=0 时, 即只有个性特征部分参与等级评估的情况, 每种实验的评估准确率都较低. 如图12所示, 当λ 逐渐增加, 评估准确率开始提高, 其中, 在实验4、实验5、实验6、实验8中, 随着λ 超过0.25, 评估准确率逐渐提升. 在实验2和实验3中, 当λ 达到0.55时, 评估准确率逐渐提升. λ 增加到一定程度后, 评估准确率会有所下降, 例如, 在实验6至实验9中, 当共性权重因子增加至0.9时, 评估准确率出现下降情况. 在实验10中, 当共性权重因子增加至0.75时, 评估准确率开始下降. 综上所述, 为了使等级评估结果在不同故障信息已知的情况下都相对最优, λ 的合理范围选择为0.55至0.75, 本文中λ=0.6。

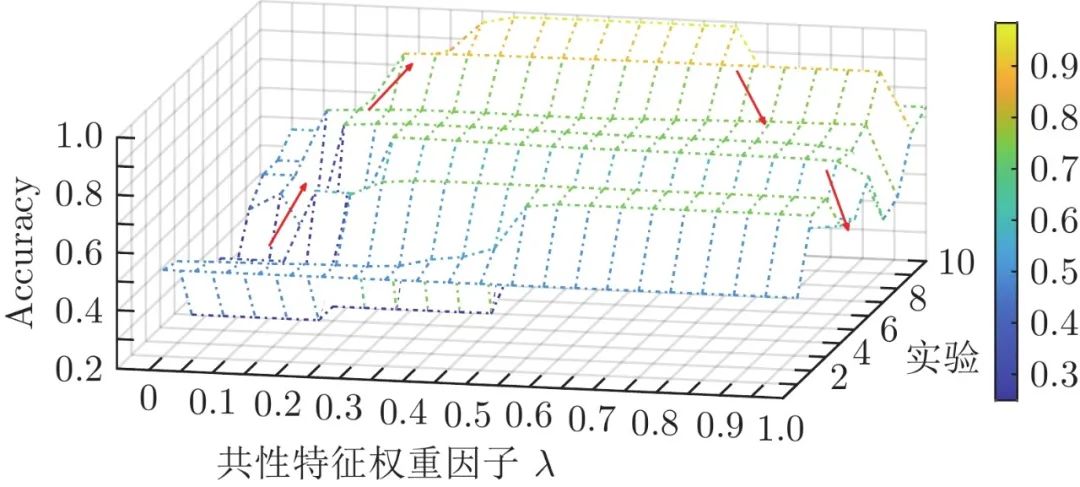
图 12  共性特征权重因子分析

应用结果验证可知, CS-DBN方法可以通过深度挖掘热连轧多规格带钢生产过程数据间的共性特征和个性特征, 构建更适合于多模态过程的故障等级评估模型. 该方法在故障等级数据不充分的情况下, 利用不同模态数据的共性故障特征同样能取得较好的等级评估结果.

4.3.4   模型鲁棒性分析

本文的鲁棒性可从两个方面进行分析. 首先, 与线性共性–个性特征提取方法相比, 当数据出现缺失或离群值时, 传统方法通过构建投影空间或基向量来提取特征, 容易导致投影空间获取偏差, 进而无法获取准确的共性–个性特征, 而CS-DBN采用了神经网络的方法, 通过非线性激活函数和训练过程的dropout技术, 可以使训练数据中离群值的影响较小, 提高了方法在低质量工业数据建模中的鲁棒性. 其次, CS-DBN可以通过增加训练过程的模态数量来更新所提取的共性特征和个性特征, 因此当测试数据为未参与训练的数据时, 模型也能有良好的共性–个性特征提取结果. 以本文验证过程为例, 一个时间段内采集的10个批次的热连轧过程数据为数据集, 其中每个批次有各自的轧制过程设定. 实验过程选择其中的部分模态为训练集, 另一部分作为测试集, 通过增加或减少参与训练的模态数据提取模态的共性特征和个性特征. 验证结果表明, 当参与训练模态的数为4时, 提取的共性–个性特征已经能较好地覆盖这10个模态的信息, 有较好的故障等级评估结果. 但是由于本文所提模型仍具有一定局限性, 当过多模态数据参与模型训练时, 网络复杂度会提高, 特征提取的结果也会有所影响, 因此, 本文的实验验证选择4个模态进行训练.

5.   结论

本文针对多模态过程的故障等级评估问题, 提出一种基于CS-DBN的故障等级评估方法. 首先, 在传统DBN基础上, 结合MK-MMD分布度量构建了CS-DBN模型, 以解决多模态过程中共性–个性特征提取问题. 同时, 融合多模态共性特征和个性特征构建了基于加权逻辑回归的故障等级评估模型. 本文将所提出的方法应用到热连轧多规格带钢的生产过程中, 并利用热连轧过程故障注入系统生成多规格带钢多种故障等级数据进行方法验证. 验证结果表明, 与传统评估方法相比, 所提方法在故障等级信息缺失下能够提高评估准确性; 当多模态故障等级信息充足时, 评估准确率可达98.75%.

未来将针对其他深度学习算法进行改进和优化, 提升多模态过程故障等级评估的精度, 并对复合故障下的多标签评估与分类方法开展研究.

声明:公众号转载的文章及图片出于非商业性的教育和科研目的供大家参考和探讨，并不意味着支持其观点或证实其内容的真实性。版权归原作者所有，如转载稿涉及版权等问题，请立即联系我们删除。

“人工智能技术与咨询”  发布