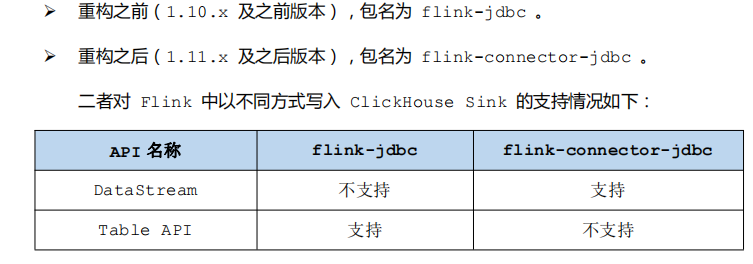
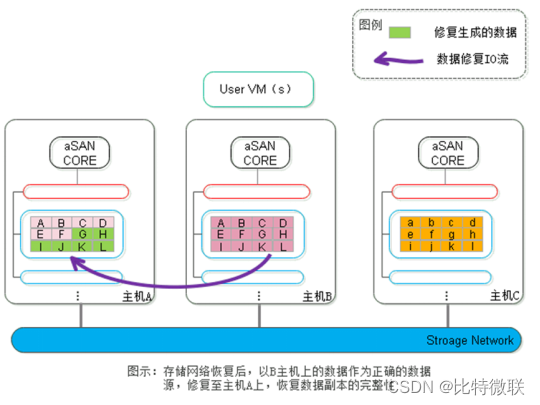
一、线性规划简介
线性规划通俗讲就是“有限的资源中获取最大的收益”(优化类问题)。而且所有的变量关系式都是线性的,不存在x²、指数函数、对数函数、反比例函数、三角函数等。此模型要优化的就是在一组线性约束条件下,求线性目标函数的最大值和最小值。
二、适用赛题
题目中提到“XXX有多少”“怎样安排/分配”“最多(少)”“利润最大”等词。如怎样生产安排使总利润最大、怎样投资使总收益最大、怎样运输使总运费最少等。
注意:在投资类问题中,收益率 = 收益 / 成本,如果要求总收益最大,一般可以用线性规划;如果要求总收益率最大,一般是非线性规划。
判断标准就是所有变量是否是一次方。
三、模型流程

四、流程解析
1.条件假设
这个需要具体题目具体分析,有些题目通过一些前提条件假设可以很好地简化题目。
2.提取要素
①决策变量
就是提取出题目中的所有变量。
②目标函数
我们需要求得的值,比如需要使利润最大,目标函数就是利润的表达式。
③约束条件
通过题目提取出各个变量的范围。
3.调用函数
调用MATLAB自带的linprog函数。
[x, fval] = linprog(f, A, b, Aeq, beq, lb, ub)
| f | 目标函数的系数向量(必须是求最小值形式下的) |
| A, b | 不等式约束条件的变量系数矩阵和常系数矩阵(必须是<或<=形式下的) |
| Aeq, beq | 等式约束条件的系数矩阵和常系数矩阵 |
| lb, ub | 决策变量的最小取值和最大取值 |
- 等号左边的x返回最优解的变量取值,fval返回目标函数的最优值
- 注意:要调用linprog函数,填入的变量必须是取自MATLAB标准型的形式
- MATLAB标准型:模型的目标函数是求最小值、约束条件都是小于等于或等于
最终求解出最优解


![[职场] 会计学专业学什么 #其他#知识分享#职场发展](https://img-blog.csdnimg.cn/img_convert/8b7b90170669d1244af867a4e03cf6d5.jpeg)




![[office] Excel2019函数MAXIFS怎么使用?Excel2019函数MAXIFS使用教程 #知识分享#微信#经验分享](https://img-blog.csdnimg.cn/img_convert/358b3daf7ce7e4ef6c937fed9fb7529b.jpeg)