话不多说，直接看题：

首先，这个不是按照字典序的顺序，而是以只要1先做，在满足后让2先做。。。。

就是让数字小的放前面做+拓扑排序。

我们可以先做1，看看它的前驱。

举个例子：

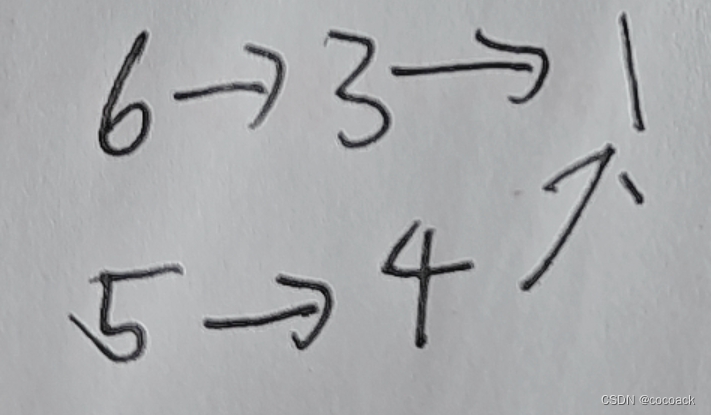
我们肯定要把1放前面做，然后就确定把1的前驱及其相连放前面。

我们再看2，2没有，那就把2的前驱及其相连放1后面。

看3，我们把3，6放最前面，同理，把5，4放在3后面，于是我们可以得到63541.

我们发现这样子实现起来比较困难，这是因为限制关系造成的，我们知道首先要选的肯定在无前驱的点上，但至于要哪个无法根据现在的情况推断，这就造成了实现的复杂性。

于是，我们可以反着看，我们把边反一下，把取第1个的思路换成取倒数第n个，这样子，最后一个肯定在无前驱的点上，而我们只要选其中max的，然后再根据它解锁倒数第2个的可能的点。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int d,n,m,x,y,ans[100010],inc[100010],head[100010],cnt;
struct node{int next,dian;
}edge[100010];
priority_queue<int> q;
void merge(int x,int y){edge[++cnt].dian=y;edge[cnt].next=head[x];head[x]=cnt;
}
bool tuopu(){while(!q.empty()) q.pop();for(int i=1;i<=n;i++){if(inc[i]==0){q.push(i);}}int ck=0;while(!q.empty()){int hh=q.top();q.pop();ans[++ck]=hh;for(int i=head[hh];i!=-1;i=edge[i].next){inc[edge[i].dian]--;if(inc[edge[i].dian]==0) q.push(edge[i].dian);}}if(ck<=n-1) return 0;else return 1;
}
int main(){cin>>d;while(d--){scanf("%d%d",&n,&m);memset(head,-1,sizeof(head));memset(inc,0,sizeof(inc));cnt=0;for(int i=1;i<=m;i++){scanf("%d%d",&x,&y);merge(y,x);inc[x]++;}if(tuopu()==0) printf("Impossible!\n");else{for(int i=n;i>=1;i--) printf("%d ",ans[i]);cout<<endl;}}
}

让我们再了解一下超级源点的应用吧：

我们再添加一个点使他与k个点的距离为0，因此，问题就转化成了单源点的问题，跑个迪杰斯特拉即可。

接题：

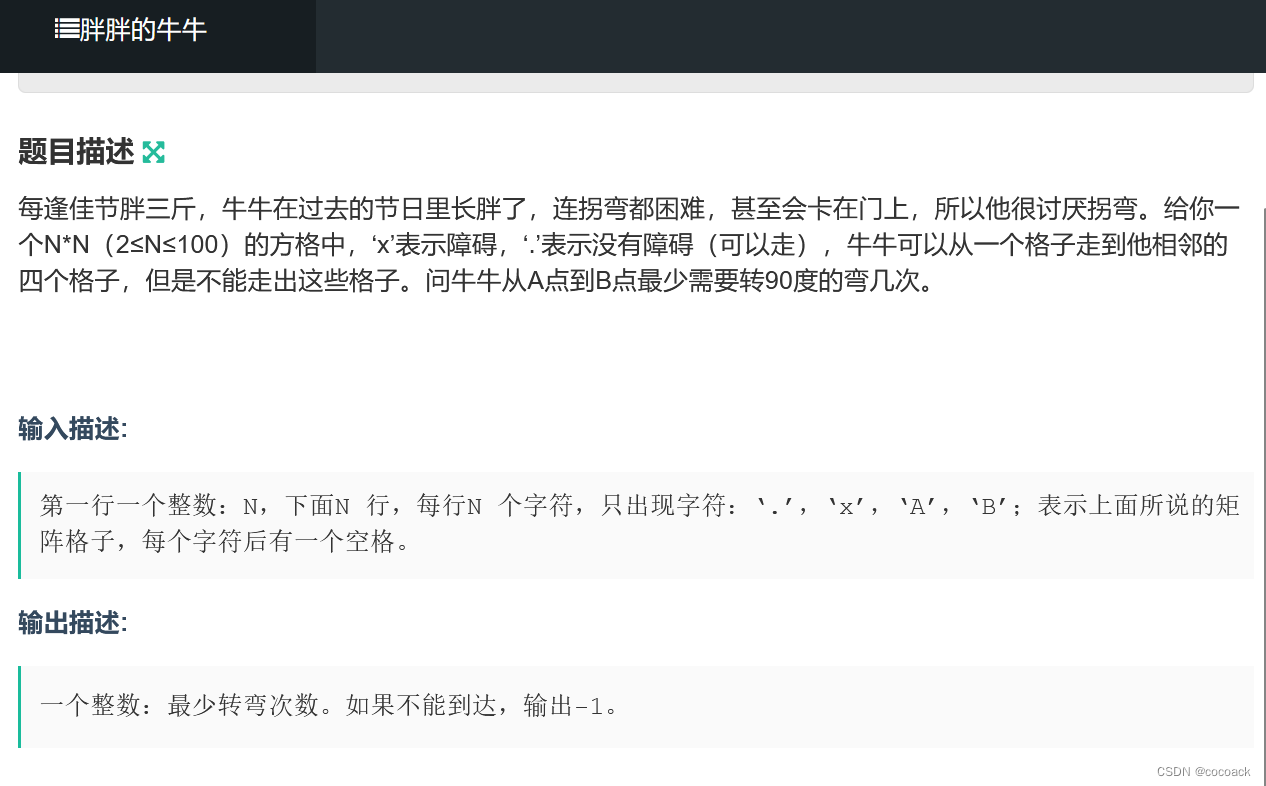
法1.BFS：

我们再记录一下当前走的方向，以转弯次数为顺序，用0/1BFS即可。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int n,zx,zy,sx,sy;
char a[105][105],c;
bool vis[105][105];
struct node{int x,y,dir,ci;
}qi;
int di[4][2]={{1,0},{-1,0},{0,1},{0,-1}};
deque<node> q;
int bfs(node qi1){memset(vis,0,sizeof(vis));if(!q.empty()) q.pop_back();q.push_front(qi1);while(!q.empty()){node ck=q.front();vis[ck.x][ck.y]=1;q.pop_front();if(ck.x==zx&&ck.y==zy) {return ck.ci;}for(int i=0;i<4;i++){node hh;hh.x=ck.x+di[i][0];hh.y=ck.y+di[i][1];if(hh.x<=0||hh.y<=0||hh.x>n||hh.y>n) continue;if(a[hh.x][hh.y]=='x') continue;if(vis[hh.x][hh.y]==1) continue;if(ck.dir==abs(di[i][0])){q.push_front({hh.x,hh.y,ck.dir,ck.ci});}else{q.push_back({hh.x,hh.y,1-(ck.dir),ck.ci+1});  }}}return -1;
}
int main(){cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>c;a[i][j]=c;if(c=='A'){sx=i;sy=j;}if(c=='B'){zx=i;zy=j;}}}int a1=bfs({sx,sy,1,0});int b1=bfs({sx,sy,0,0});if(a1==-1||b1==-1) cout<<max(a1,b1);else cout<<min(a1,b1);
}

法2.建图：

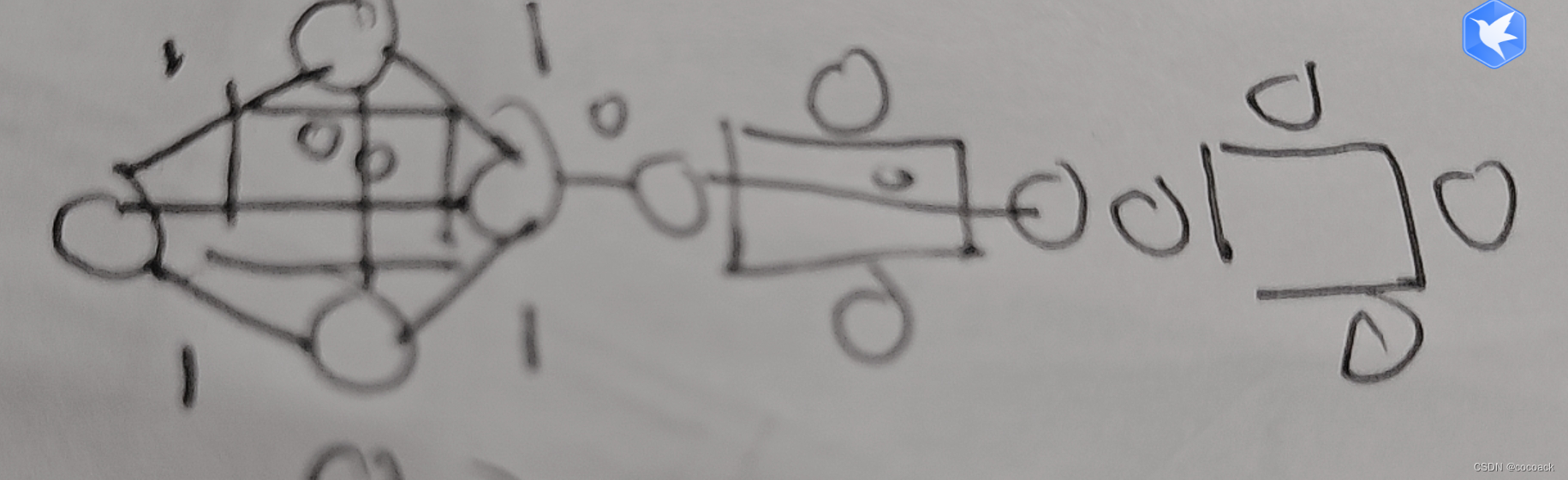
下面为AC代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,sx,sy,zx,zy;
char a[105][105],c;
int head[100000],cnt;
struct node{int dian,len,next;
}edge[500000];
void merge(int x,int y,int v){edge[++cnt].dian=y;edge[cnt].len=v;edge[cnt].next=head[x];head[x]=cnt;
}
int dis[40000+10];
bool vis[40010];
struct ty{int dian,dis1;bool operator<(const ty &a) const{return dis1>a.dis1;}
};
priority_queue<ty> q;
int dij(int s,int t){q.push({s,0});dis[s]=0;while(!q.empty()){ty ck=q.top();q.pop();if(vis[ck.dian]==1) continue;vis[ck.dian]=1;for(int i=head[ck.dian];i!=-1;i=edge[i].next){int i1=edge[i].dian;if(vis[i1]==1) continue;if(dis[i1]>dis[ck.dian]+edge[i].len){dis[i1]=dis[ck.dian]+edge[i].len;q.push({i1,dis[i1]});}}}if(dis[t]>=0x3f) return -1;else return dis[t];}
signed main(){cin>>n;memset(dis,0x3f,sizeof(dis));memset(head,-1,sizeof(head));for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>c;a[i][j]=c;if(c=='A'){sx=i;sy=j;}if(c=='B'){zx=i;zy=j;}}}for(int i=1;i<=n*n;i++){for(int j=1;j<=4;j++){for(int k=1;k<=4;k++){if(k!=j){if((k+j)%2==0)  merge(4*(i-1)+j,4*(i-1)+k,0);else merge(4*(i-1)+j,4*(i-1)+k,1);}}}}for(int i=1;i<=n;i++){for(int j=2;j<=n;j++){if(a[i][j]=='x'||a[i][j-1]=='x'){merge((i-1)*4*n+(j-1)*4+1,(i-1)*4*n+(j-1)*4-1,0x3f);merge((i-1)*4*n+(j-1)*4-1,(i-1)*4*n+(j-1)*4+1,0x3f);}else{merge((i-1)*4*n+(j-1)*4+1,(i-1)*4*n+(j-1)*4-1,0);merge((i-1)*4*n+(j-1)*4-1,(i-1)*4*n+(j-1)*4+1,0);}}}for(int i=1;i<=n;i++){for(int j=2;j<=n;j++){if(a[j][i]=='x'||a[j-1][i]=='x'){merge((j-1)*4*n+(i-1)*4+2,(j-2)*4*n+(i-1)*4+4,0x3f);merge((j-2)*4*n+(i-1)*4+4,(j-1)*4*n+(i-1)*4+2,0x3f);}else{merge((j-1)*4*n+(i-1)*4+2,(j-2)*4*n+(i-1)*4+4,0);merge((j-2)*4*n+(i-1)*4+4,(j-1)*4*n+(i-1)*4+2,0);}}}for(int i=1;i<=4;i++) merge(n*n*4+1,4*(n*sx+sy-n-1)+i,0);for(int i=1;i<=4;i++) merge(4*(n*zx+zy-n-1)+i,n*n*4+2,0);cout<<dij(n*n*4+1,n*n*4+2);
}