第 124 场 LeetCode 双周赛题解

A 相同分数的最大操作数目 I

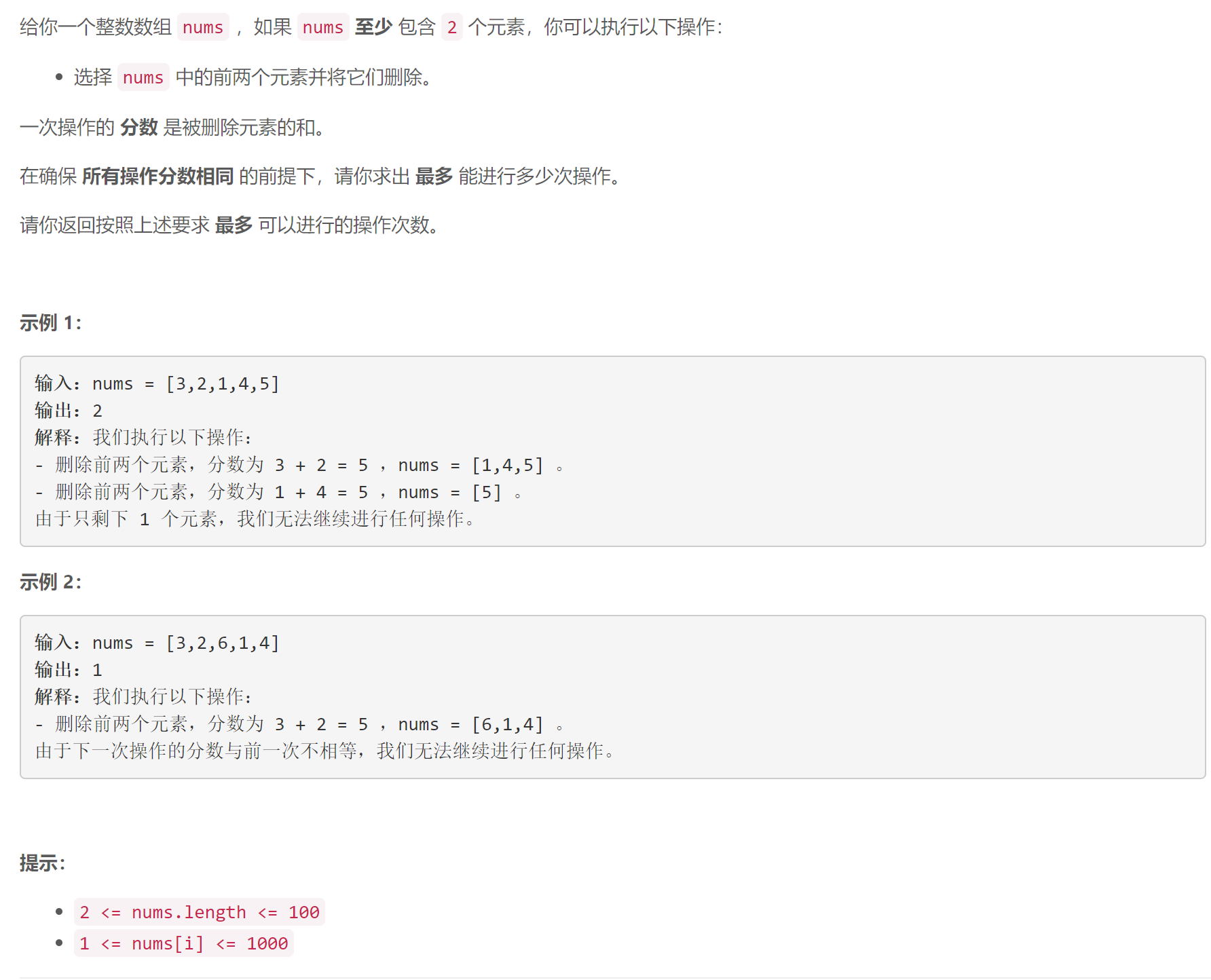
模拟

class Solution {
public:int maxOperations(vector<int> &nums) {int n = nums.size();int s = nums[0] + nums[1];int res = 1;for (int i = 2; i + 1 < n; i += 2)if (nums[i] + nums[i + 1] == s)res++;elsebreak;return res;}
};

B 进行操作使字符串为空

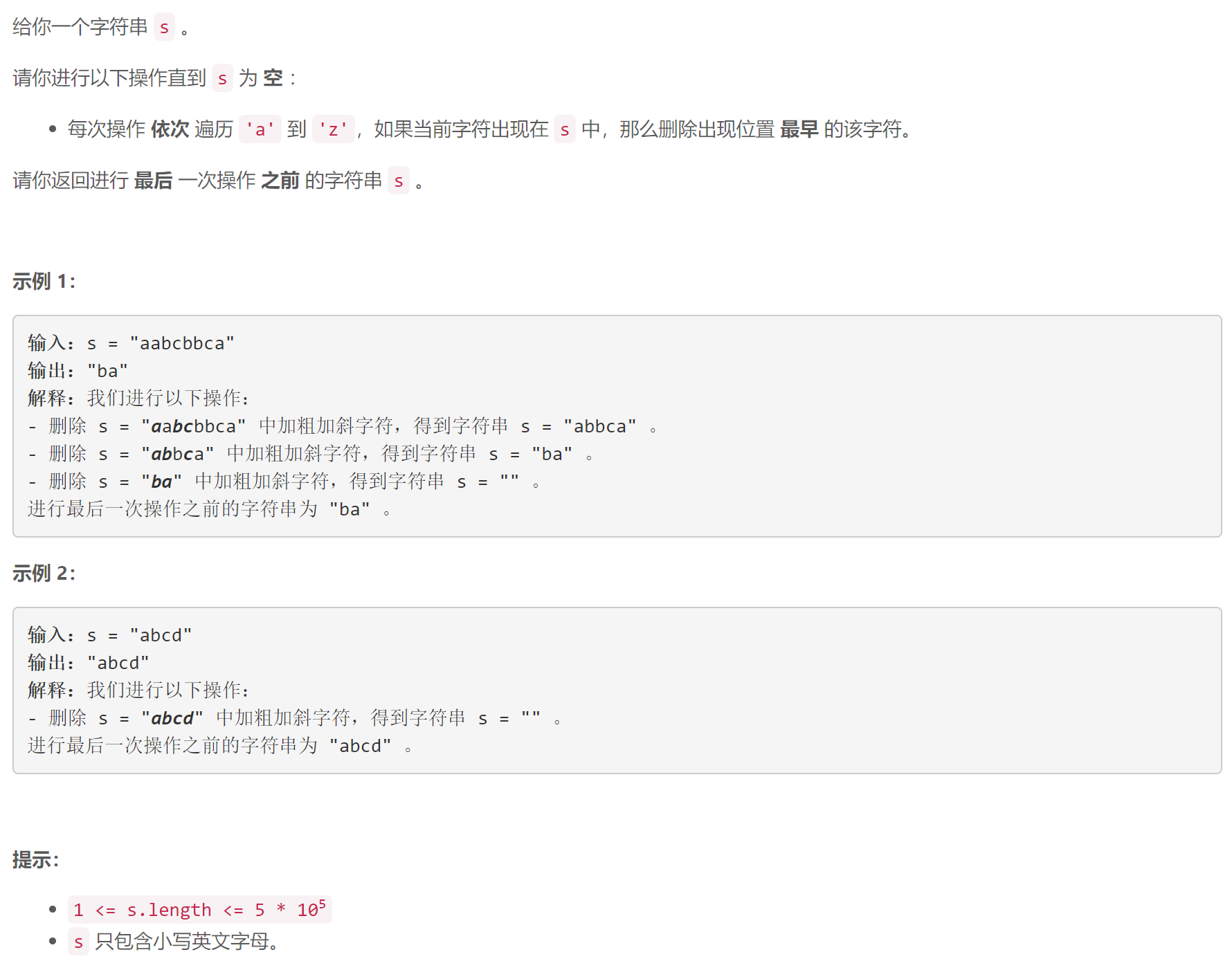
计数：记录各字符的出现次数，出现次数最大的各字符的最右位置形成最后一次操作之前的 $s$

class Solution {
public:string lastNonEmptyString(string s) {vector<int> cnt(26);for (auto c: s)cnt[c - 'a']++;int mx = *max_element(cnt.begin(), cnt.end());string res;for (int i = s.size() - 1; i >= 0; i--)if (cnt[s[i] - 'a'] == mx) {cnt[s[i] - 'a'] = 0;res.push_back(s[i]);}reverse(res.begin(), res.end());return res;}
};

C 相同分数的最大操作数目 II

动态规划：设 $p [l] [r] [t a g]$ 为数组 $n u m s [l, r]$ 在之前各次操作分数都为 $s [t a g]$ 的情况下，最多可以进行的操作次数，实现通过记忆化搜素进行状态转移

class Solution {
public:int maxOperations(vector<int> &nums) {int n = nums.size();int p[n][n][3];memset(p, -1, sizeof(p));//初始化标志vector<int> s(3);s[0] = nums[0] + nums[1];s[1] = nums[n - 2] + nums[n - 1];s[2] = nums[0] + nums[n - 1];function<int(int, int, int)> dfs = [&](int l, int r, int tag) {//记忆化搜素if (l > r)return 0;if (p[l][r][tag] != -1)return p[l][r][tag];if (r - l + 1 < 2)return p[l][r][tag] = 0;int tar = s[tag];//一次操作的分数p[l][r][tag] = 0;if (nums[l] + nums[l + 1] == tar)//删除最前面两个元素p[l][r][tag] = max(p[l][r][tag], 1 + dfs(l + 2, r, tag));if (nums[r - 1] + nums[r] == tar)//删除最后面两个元素p[l][r][tag] = max(p[l][r][tag], 1 + dfs(l, r - 2, tag));if (nums[l] + nums[r] == tar)//删除第一个和最后一个元素p[l][r][tag] = max(p[l][r][tag], 1 + dfs(l + 1, r - 1, tag));return p[l][r][tag];};int res = 0;for (int k = 0; k < 3; k++)//第一次操作时可以进行三种删除res = max(res, dfs(0, n - 1, k));return res;}
};

D 修改数组后最大化数组中的连续元素数目

排序 + 哈希：先对 $n u m s$ 排序，然后逆序遍历 $n u m s [i]$ ，设 $p [x]$ 为数组 $n u m s [i + 1, n u m s . s i ze () - 1]$ 中起始元素为 $x$ （包括通过 +1 得到 $x$ 的情况）的最大连续元素数目，遍历过程中更新哈希表 $p$

class Solution {
public:int maxSelectedElements(vector<int> &nums) {sort(nums.begin(), nums.end());int n = nums.size();int res = 1;unordered_map<int, int> p;for (int i = n - 1; i >= 0; i--) {p[nums[i]] = p.count(nums[i] + 1) ? p[nums[i] + 1] + 1 : 1;//nums[i]不变的情况res = max(res, p[nums[i]]);p[nums[i] + 1] = p.count(nums[i] + 2) ? p[nums[i] + 2] + 1 : 1;//nums[i]+1的情况res = max(res, p[nums[i] + 1]);}return res;}
};