Day 29

01. 非递减子序列（No. 491）

题目链接

代码随想录题解

1.1 题目

给你一个整数数组 nums ，找出并返回所有该数组中不同的递增子序列，递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。

数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。

示例 1：

输入：nums = [4,6,7,7]
输出：[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]

示例 2：

输入：nums = [4,4,3,2,1]
输出：[[4,4]]

提示：

• 1 <= nums.length <= 15
• -100 <= nums[i] <= 100

1.2 笔记

看完题目，很容易就可以发现，递增子序列就是 符合递增条件的子集，而且其中会包含重复元素，这就和昨天做到的题目 子集 II 十分相似，建议做完这道题再来看本题的题解

代码随想录刷题笔记 DAY 28 | 复原 IP 地址 No.93 | 子集 No.78 | 子集 II No.90

但是有一个很大的坑：

递增子序列是无法通过排序来去重的

回顾一下子集中如果出现重复的元素的去重方式

[1 2 2] ，将这个数组进行排序如果一层中遇到相同的元素就进行 continue

但递增子序列的问题就是它的顺序是固定的，不能通过排序来去重。

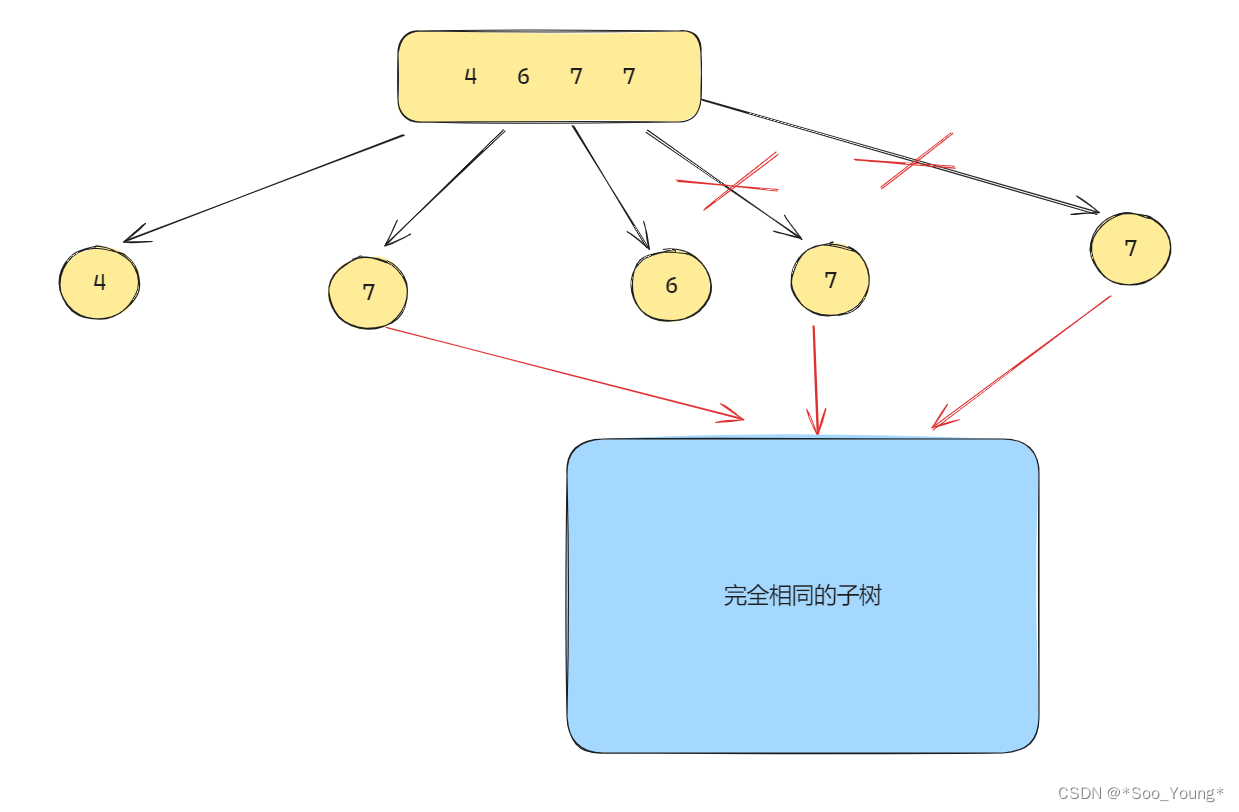
比如说如上的这种情况，所有的节点都会去遍历相同的子树，这就导致了重复。

所以要做的是 层内去重，但是又不能通过排序的方式，所以我们可以想到在每一层去声明一个 record 当发现后续遍历的内容已经在 record 中出现的时候就跳过本次遍历。

这个 record 可以采用哈希方式实现，也可以使用列表方式去实现，显然哈希的实现方式更好

    public void backtracking(int index, int[] nums) {if (index > nums.length - 1) {return;}int[] record = new int[300];for (int i = index; i < nums.length; i++) {// 去重操作if (i > index && record[nums[i]+100] > 0) {continue;} else {record[nums[i] + 100] = 1;}// ...}}

因为 nums[i] 的范围是在 -100 到 100 的范围内的，所以这里将 nums[i] + 100 存入数组，避免出现越界的情况。

这样就完成了层内的去重，剩下的就是考虑如何保证递增了。

显然这里也有两种选择：

• 写一个方法，每次去判断 path 是否符合
• 在递归过程中去判断

先来看比较容易理解的第一个方法

 public boolean isValid(List<Integer> path) {if (path.size() <= 1) {return false;}int currentMax = Integer.MIN_VALUE;for (int i : path) {if(i < currentMax) {return false;} else {currentMax = i;}}return true;
}

判断一个列表是否非递减，只需要在递增中不断更新 currentMax 并且确定后面的元素是否大于等于这个 current 即可。

在递归中也是相同的思路，只需要判断 nums[i] 是否大于等于 path.get(size() - 1) 也就是最后一个元素即可，否则，同样 continue。

    if (!path.isEmpty() && nums[i] < path.get(path.size() - 1)) {continue;} else {record[nums[i] + 100] = 1;}

将这段代码和上面去重的代码组成一个 if 语句，写出代码。

1.3 代码

class Solution {List<Integer> path = new ArrayList<>();List<List<Integer>> res = new ArrayList<>();public List<List<Integer>> findSubsequences(int[] nums) {backtracking(0, nums);return res;}public void backtracking(int index, int[] nums) {if (index > nums.length - 1) {return;}int[] record = new int[300];for (int i = index; i < nums.length; i++) {// 去重操作if (i > index && record[nums[i]+100] > 0 ||!path.isEmpty() && nums[i] < path.get(path.size() - 1)) {continue;} else {record[nums[i] + 100] = 1;}path.add(nums[i]);if (path.size() > 1) {res.add(new ArrayList(path));}backtracking(i+1, nums);path.remove(path.size() - 1);}}
}

02. 全排列（No. 46）

题目链接

代码随想录题解

2.1 题目

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示：

• 1 <= nums.length <= 6
• -10 <= nums[i] <= 10
• nums 中的所有整数 互不相同

2.2 笔记

上面说到过，回溯法可以解决排列问题，这就是一个经典的例子。

当遇到一开始思路不明确的回溯的题，建议大家先把树形结构画出来，这样各种操作就一目了然了。

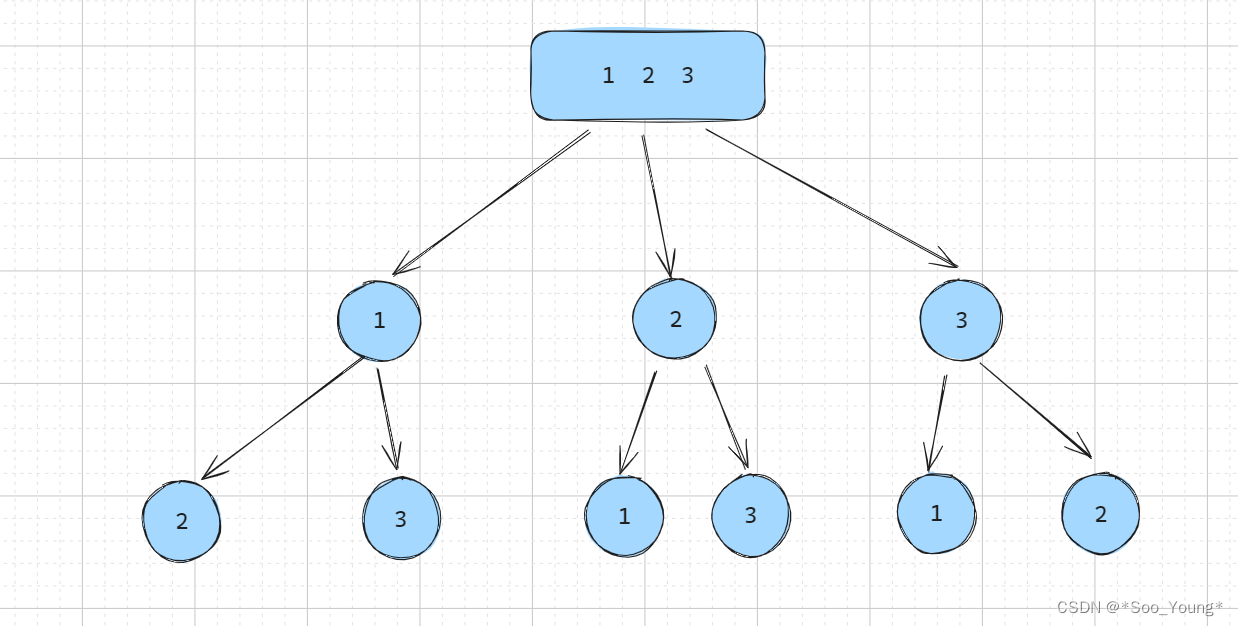
遍历到 1 之后就只能遍历 2 和 3 了，也就是每次遍历到一个节点，在这个节点剩余的遍历过程中，这个节点的值都不能出现，即在数组中删除掉这个遍历过的数。

但在数组中删除的操作时间复杂度相当高，所以很明显需要用到标记数组的方法。

与上题区分开，这里使用 boolean 数组

因为这里的去重是在路径中的，对全局的去重，所以标记数组的声明需要在层外

    boolean[] used;public List<List<Integer>> permute(int[] nums) {used = new boolean[30];// ...}public void backtracking(int[] nums) {// ...}

当路径中遇到遍历过的内容的时候就跳过

		for (int i = 0; i < nums.length; i++) {if (used[nums[i] + 10]) {continue;}// ...}

如果大家做过一些回溯的题目，很容易发现当层内去重的时候就不需要回溯，而路径去重就需要回溯，因为层内去重是在一层 for 循环中做的。

递归的终点，很显然就是当收集的数量等于数组长度的时候。

        if (path.size() == nums.length) {res.add(new ArrayList(path));return;}

写出代码

2.3 代码

class Solution {List<Integer> path = new ArrayList<>();List<List<Integer>> res = new ArrayList<>();boolean[] used;public List<List<Integer>> permute(int[] nums) {used = new boolean[30];backtracking(nums);return res;}public void backtracking(int[] nums) {if (path.size() == nums.length) {res.add(new ArrayList(path));return;}for (int i = 0; i < nums.length; i++) {if (used[nums[i] + 10]) {continue;}path.add(nums[i]);used[nums[i] + 10] = true;backtracking(nums);path.remove(path.size() - 1);used[nums[i] + 10] = false;}}
}

03. 全排列 II（No. 47）

题目链接

代码随想录题解

3.1 题目

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],
[1,2,1],
[2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

• 1 <= nums.length <= 8
• -10 <= nums[i] <= 10

3.2 笔记

做过上一题的朋友不用猜也能知道这个题要考察的是什么

就是在数组中加上重复的元素，考察层内去重的问题

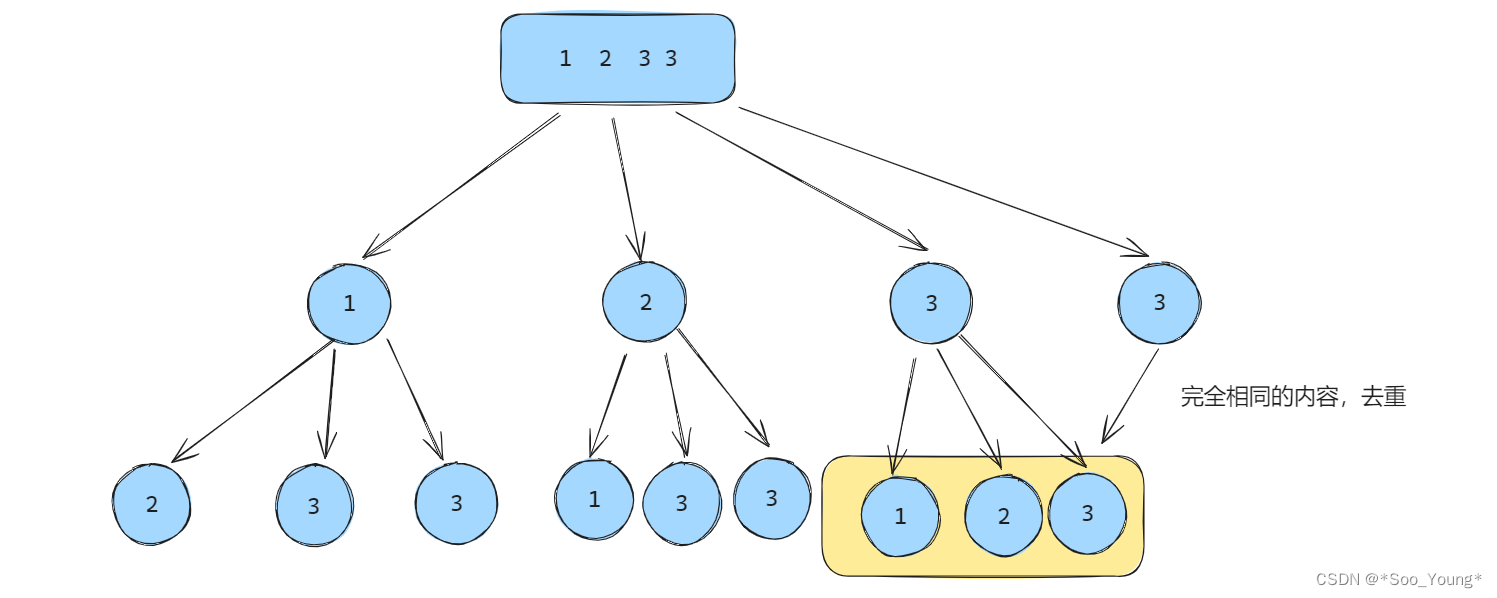
所以这道题除了上题的路径去重还需要添加上层内去重。

但路径去重的时候应该注意，不能再以 nums[i] 作为标识了，因为内部含有相同的元素，所以应该使用 i 下标作为去重的标识。

		for (int i = 0; i < nums.length; i++) {if (used[i]) {continue;}// ...}

然后只需要加上层内去重的代码就大功告成了

本题几乎没有新的内容，只需要注意路径去重的逻辑即可。

3.3 代码

class Solution {List<Integer> path = new ArrayList<>();List<List<Integer>> res = new ArrayList<>();boolean[] used;public List<List<Integer>> permute(int[] nums) {used = new boolean[30];backtracking(nums);return res;}public void backtracking(int[] nums) {if (path.size() == nums.length) {res.add(new ArrayList(path));return;}for (int i = 0; i < nums.length; i++) {if (used[nums[i] + 10]) {continue;}path.add(nums[i]);used[nums[i] + 10] = true;backtracking(nums);path.remove(path.size() - 1);used[nums[i] + 10] = false;}}
}