1. 基础位运算
位运算符是在二进制位级别上对数据进行操作的运算符。以下是一些常见的位运算符:
1. 右移运算符 (>>)
将一个数的所有二进制位向右移动指定的位数。右移运算符 >> 表示将运算符左边的操作数的所有位向右移动右边指定的位数,右边多余的位将被丢弃,左边用符号位填充。
int x = 8; // 二进制: 0000 1000
int result = x >> 2; // 二进制: 0000 0010,即十进制的 22. 左移运算符 (<<)
将一个数的所有二进制位向左移动指定的位数。左移运算符 << 表示将运算符左边的操作数的所有位向左移动右边指定的位数,左边多余的位将被丢弃,右边用零填充。
int x = 8; // 二进制: 0000 1000
int result = x << 2; // 二进制: 0010 0000,即十进制的 32
3. 按位取反运算符 (~)
对一个数的每个二进制位执行取反操作,即将 0 变为 1,将 1 变为 0。
int x = 5; // 二进制: 0000 0101
int result = ~x; // 二进制: 1111 1010,即十进制的 -6
4. 按位或运算符 (|)
对两个数的每个二进制位执行按位或操作,只要有一个为 1,结果位就为 1。
int x = 5; // 二进制: 0000 0101
int y = 3; // 二进制: 0000 0011
int result = x | y; // 二进制: 0000 0111,即十进制的 7
5. 按位与运算符 (&)
对两个数的每个二进制位执行按位与操作,只有两个都为 1,结果位才为 1。
int x = 5; // 二进制: 0000 0101
int y = 3; // 二进制: 0000 0011
int result = x & y; // 二进制: 0000 0001,即十进制的 1
6. 按位异或运算符 (^)
对两个数的每个二进制位执行按位异或操作,如果两个位不同则结果位为 1,相同则为 0。或者可以简单记忆为无进位相加。
int x = 5; // 二进制: 0000 0101
int y = 3; // 二进制: 0000 0011
int result = x ^ y; // 二进制: 0000 0110,即十进制的 6
2. 位图
位图(Bitmap)是一种用于表示二进制数据的数据结构,通常用于表示一组二进制位的状态。它的核心思想是用二进制位的值(0或1)来表示某种状态或信息。它的主要核心操作即以下三步
1. 给定一个数n,确定它的二进制表示中的第x位是0还是1
要想判断某一个位置是0还是1只需要对这个位置&上一个1,如果该位置为1则结果为1,反之则结果为0,在这里我们要想快速判断可以使用
(n >> x) & 12. 将一个数n的二进制表示的第x位修改成1
要想修改x位置的值为1,只需要对这个位置|上一个1,其余位置|上0,这样就可以将该位置修改成1,即
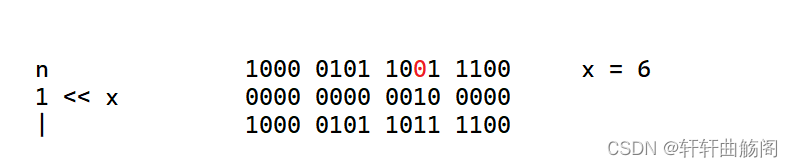
在这里我们要想快速修改可以使用
(1 << x) | n3. 将一个数n的二进制表示的第x位修改成0
要想修改x位置的值为0,只需要对这个位置&上一个0,其余位置&上1,这样就可以将该位置修改成0,即

在这里我们要想快速修改可以使用
(~(1 << x)) & n4. 位图的思想
从使用上来说,位图其实与哈希表相似只不过哈希表是创建一个数组来存储信息,而位图则是使用比特位中的0与1来存储信息。
3. 提取与删除二进制中最右侧的1
1. 提取(lowbit)
要想提取最右侧的0,只需要让n & -n,即

可以看到,这个操作的本质就是将最右侧的1的左边区域全部变为相反的数
2. 删除
要想提取最右侧的0,只需要让n & (n - 1),即

可以看到,这个操作的本质是将最右侧的1的右边区域(包含1)全部变为相反数
4. 异或运算(^)的运算律
异或运算律如下
1. a ^ 0 = a
2. a ^ a = 0
3. a ^ (b ^ c) = (a ^ b) ^ c
5. 应用实例
1. 位1的个数
题目链接:191. 位1的个数 - 力扣(LeetCode)

解析:根据题意我们可以使用删除最右侧的1操作来统计个数,代码如下
class Solution
{
public:int hammingWeight(uint32_t n) {int num = 0;while (n){num++;n &= (n - 1);} return num;}
};2. 比特位计数
题目链接:338. 比特位计数 - 力扣(LeetCode)

解析:这道题也可以使用删除最右侧的1策略来统计,代码如下
class Solution
{
public:vector<int> countBits(int n) {vector<int> ret;for (int i = 0; i <= n; i++){int num = 0, cur = i;while (cur){num++;cur &= (cur - 1);}ret.push_back(num);}return ret;}
};3. 汉明距离
题目链接:461. 汉明距离 - 力扣(LeetCode)

解析:这里我们需要求得不同的二进制位个数,由于异或操作可以达到相异为1,相同为0的效果,我们只需要将两个数异或并统计异或后1的数量即可,代码如下
class Solution
{
public:int hammingDistance(int x, int y) {int ret = 0;int tmp = x ^ y;while (tmp){ret++;tmp &= (tmp - 1);}return ret;}
};4. 只出现一次的数字
题目链接:136. 只出现一次的数字 - 力扣(LeetCode)

解析:这道题我们可以利用异或的性质,由于只有一个数出现次数为1次,其余数出现次数均为2次,我们只需要将他们全部异或起来就能得到结果,代码如下
class Solution
{
public:int singleNumber(vector<int>& nums) {int res = 0;for (auto e : nums) res ^= e;return res;}
};5. 只出现一次的数字Ⅲ
题目链接:260. 只出现一次的数字 III - 力扣(LeetCode)

解析:这道题中,有两个数字只出现一次(这里以3(011)和5(101)举例),那么将所有的数异或起来之后,会得到这两个数的异或结果(6(110)),由于异或的性质是相异为1,所以我们可以提取最右边的1(这个1代表3和5在这个位置不同),以它作为标志将整个数组分为2组,再次分别将所有数据异或便可以得到结果,代码如下
class Solution
{
public:vector<int> singleNumber(vector<int>& nums) {int tmp = 0;for (int e : nums) tmp ^= e;// 取得最后一位1// 当tmp为INT_MIN时,即负数的最高位为 1,直接对其取反会导致溢出,需要特殊判断int flag = tmp == INT_MIN ? tmp : tmp & (-tmp);int e1 = 0, e2 = 0;for (int e : nums){if (flag & e) e1 ^= e;else e2 ^= e;}return { e1, e2 };}
};