欠定方程组及其求解

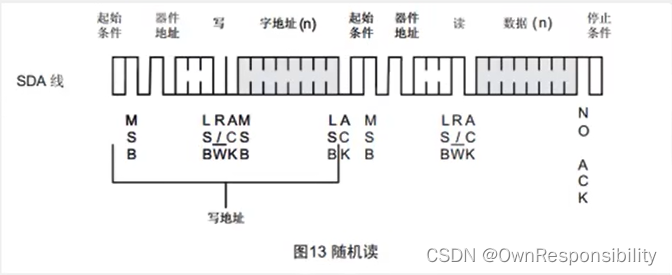
欠定方程组是指方程的数量少于未知数的数量的方程组。在这种情况下，通常有无限多个解，因为给定的方程不足以唯一确定所有未知数的值。在某些情况下，我们可以利用额外的信息或假设，如稀疏性或其他约束，来找到一个合理的解。

例子

举个简单的欠定方程组的例子：设有下面的两个线性方程组，描述两条直线，在二维空间中搜索交点（即x和y的值）：

2x + 3y = 5
4x + 6y = 10

显然，这个方程组是欠定的，因为第二个方程只是第一个方程的两倍，事实上，我们只有一个独立方程来解决两个未知数。这里并没有唯一的解，而是有无数个可能的解，因为任何在直线 2x + 3y = 5 上的点都是可能的解。

一种常见的数学方法来解决欠定系统是使用最小二乘法，尤其是在方程涉及噪声或误差时。在这种情况下，可以通过优化技术来求一个解，这个解在某种意义上是最优的（比如，最小化误差的平方和）。

Python仿真

在Python中，我们可以使用NumPy库中的lstsq函数（最小二乘法）来解决欠定方程组。让我们以该例子为例，使用Python求解：

import numpy as np# 系数矩阵A和向量b
A = np.array([[2, 3], [4, 6]])
b = np.array([5, 10])# 使用 NumPy 的 lstsq 函数求解最小二乘法
# rcond=None 指定了一个小于正的 float64 类型的最小值
result = np.linalg.lstsq(A, b, rcond=None)# 结果存在一个元组中，第一个元素x是解
x = result[0]print("解为:", x)

注意：np.linalg.lstsq会返回一个结果元组，其第一个元素包含最小二乘解。

在这个例子中，最小二乘法会找到一个近似解，试图满足两个方程。由于方程组是欠定的（真正只有一个独立方程），解是无数可能值中的一个，并且NumPy使用最小二乘法在该直线的解集中找到最小范数解。

结果

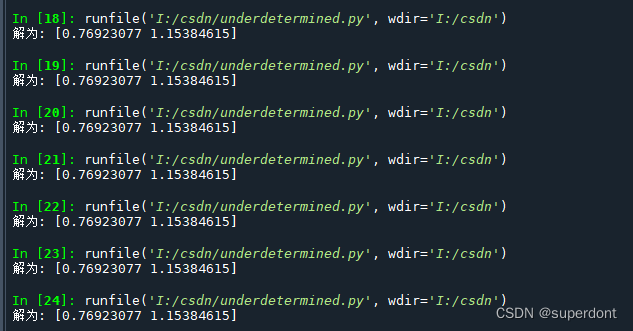
结果如下：
（运行了多次的截图，如果运行一次截图，是一个长条，看不清楚）
在这里插入图片描述

参考：numpy.linalg.lstsq

np.linalg.lstsq 是 NumPy（Numerical Python）库中用于求解最小二乘法问题的函数。最小二乘法是一种优化技术，用于寻找使一组线性方程组的残差平方和最小化的解。这在许多数学和工程应用中非常有用，特别是在处理欠定方程组或存在误差的情况下。

下面是对np.linalg.lstsq函数的详细解释及其常用参数：

语法：

numpy.linalg.lstsq(a, b, rcond='warn')

参数：

a：代表系数矩阵的二维数组（m×n），其中 m 表示方程组的数量，n 表示未知数的数量。
b：代表常数向量的数组，其长度必须为 m。
rcond：可选参数，控制奇异值的截断值。默认值为 ‘warn’，会发出奇异值警告。可以设置为 None 来禁止警告。

返回值：

x：如果方程组是欠定的，则返回残差的最小二乘解（最小范数解）。如果方程组是超定的，则返回具有最小残差平方和的最小二乘解。
residuals：对应于每个方程的残差平方和。
rank：系数矩阵的秩。
s：系数矩阵的奇异值。

功能：

np.linalg.lstsq函数使用奇异值分解（SVD）方法来求解最小二乘问题。
当系数矩阵 a 是满秩的时候，np.linalg.lstsq会给出唯一的最小二乘解。
当系数矩阵 a 的秩小于 n（未知数的数量）时，np.linalg.lstsq会返回一个近似解，该解最小化了残差的平方和，并属于最小范数解。

总之，np.linalg.lstsq函数是一个强大的工具，用于求解线性方程组的最小二乘逼近问题，特别适用于欠定或超定方程组的情况。通过调用这个函数，我们可以求解出最优的线性关系，并用于估计参数、拟合曲线等数学和工程问题中。

我的图书

下面两本书欢迎大家参考学习。

OpenCV轻松入门

李立宗，OpenCV轻松入门，电子工业出版社，2023
本书基于面向 Python 的 OpenCV(OpenCV for Python)，介绍了图像处理的方方面面。本书以 OpenCV 官方文档的知识脉络为主线，并对细节进行补充和说明。书中不仅介绍了 OpenCV 函数的使用方法，还介绍了函数实现的算法原理。

在介绍 OpenCV 函数的使用方法时，提供了大量的程序示例，并以循序渐进的方式展开。首先，直观地展示函数在易于观察的小数组上的使用方法、处理过程、运行结果，方便读者更深入地理解函数的原理、使用方法、运行机制、处理结果。在此基础上，进一步介绍如何更好地使用函数处理图像。在介绍具体的算法原理时，本书尽量使用通俗易懂的语言和贴近生活的实例来说明问题，避免使用过多复杂抽象的公式。

本书适合计算机视觉领域的初学者阅读，包括在校学生、教师、专业技术人员、图像处理爱好者。
本书第1版出版后，深受广大读者朋友的喜爱，被很多高校选为教材，目前已经累计重印9次。为了更好地方便大家学习，对本书进行了修订。
在这里插入图片描述

计算机视觉40例

李立宗，计算机视觉40例，电子工业出版社，2022
近年来，我深耕计算机视觉领域的课程研发工作，在该领域尤其是OpenCV-Python方面积累了一点儿经验。因此，我经常会收到该领域相关知识点的咨询，内容涵盖图像处理的基础知识、OpenCV工具的使用、深度学习的具体应用等多个方面。为了更好地把所积累的知识以图文的形式分享给大家，我将该领域内的知识点进行了系统的整理，编写了本书。希望本书的内容能够对大家在计算机视觉方向的学习有所帮助。
本书以OpenCV-Python（the Python API for OpenCV）为工具，以案例为载体，系统介绍了计算机视觉从入门到深度学习的相关知识点。
本书从计算机视觉基础、经典案例、机器学习、深度学习、人脸识别应用等五个方面对计算机视觉的相关知识点做了全面、系统、深入的介绍。书中共介绍了40余个经典的计算机视觉案例，其中既有字符识别、信息加密、指纹识别、车牌识别、次品检测等计算机视觉的经典案例，也包含图像分类、目标检测、语义分割、实例分割、风格迁移、姿势识别等基于深度学习的计算机视觉案例，还包括表情识别、驾驶员疲劳监测、易容术、识别年龄和性别等针对人脸的应用案例。
在介绍具体的算法原理时，本书尽量使用通俗易懂的语言和贴近生活的示例来说明问题，避免使用复杂抽象的公式来介绍。
本书适合计算机视觉领域的初学者阅读，适于在校学生、教师、专业技术人员、图像处理爱好者使用。

在这里插入图片描述