spfa通常用来求带有负权边的最短路问题，但是它还有两种特别的用法——求负环和求差分约束

求负环

我们回顾spfa算法，本质上是一个点的距离被更新以后再用它去更新其他的点。将被更新的点放入队列中，这样一直更新，直到没有任何点可以被更新后结束。形象一点，spfa实际上也相当于一层一层的扩展，但是由于有负权边，所以已经被赋值的点还会被更新而已，所以一个点如果被更新n次，那么如果没有负权回路的话，这条路径上就应该由n+1个点，但总共才n个点，很明显不成立，那么就可以证明有负权回路，也即负环。

所以要想求图中是否有负环，其实我们只要记录每个点被更新的次数即可。

在找负环的时候，最初是把所有的点都放进队列了，因为图未必连通，所以从某个点开始找，该点所在的连通块中未必有负环。同时找负环是d[]的初值也不重要了，因为我们只看更新次数，只要有负的就更新。

904. 虫洞（活动 - AcWing）

这题比较迷惑人的一点在于要在开始时间之前回到出发地，那么就有时间和空间两个维度，在时间上和空间上都要回到出发地，在空间上回去就说明图中有回路，否则无法回去，因为边权是时间，所以在时间上回去就说明有负权回路。那么看似很绕，实际上就是一个求负环的问题。

#include<bits/stdc++.h>
using namespace std;
const int N=600,M=6000;
int h[N],e[M],ne[M],w[M],idx;
int n,m,k;
int d[N],st[N],cnt[N];
void add(int a,int b,int c)
{e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
int spfa()
{memset(d,0x3f,sizeof d);memset(cnt,0,sizeof cnt);memset(st,0,sizeof st);queue<int>q;for(int i=1;i<=n;i++) {st[i]=1;q.push(i);}while(q.size()){int t=q.front();q.pop();st[t]=0;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(d[j]>d[t]+w[i]){d[j]=d[t]+w[i];cnt[j]=cnt[t]+1;//被多少个点更新if(cnt[j]>=n) return 1;if(!st[j]) st[j]=1,q.push(j);}}}return 0;
}
int main()
{int t;scanf("%d",&t);while(t--){scanf("%d%d%d",&n,&m,&k);memset(h,-1,sizeof h);idx=0;for(int i=1;i<=m;i++){int a,b,c;scanf("%d%d%d",&a,&b,&c);add(a,b,c),add(b,a,c);}for(int i=1;i<=k;i++){int a,b,c;scanf("%d%d%d",&a,&b,&c);add(a,b,-c);}if(spfa()) cout<<"YES"<<endl;else cout<<"NO"<<endl;}
}

361. 观光奶牛（361. 观光奶牛 - AcWing题库）

求f/g最大，这是典型的01分数问题。这种题的解题套路很固定，就是用二分来解：

ans=sum(f)/sum(g)

要求ans的最大值，所以ans符合要求的时候需要往大的找，那么只能是二分出来的mid小于等于ans，然后才能去找更大的。

ans>=mid

sum(f)-sum(g)*mid>=0

sum(f-g*mid)>=0

f-g*mid是什么意思呢？显然是点权-边权*mid，又要考虑点权，又要考虑边权很麻烦，所以我们可以把点权放到边权上去，即将边权变为f-g*mid，然后求正环。那么是把起始点权放上去，还是把终点权放上去呢，其实都可以，这里我们把起始点的点权放上去。

#include<bits/stdc++.h>
using namespace std;
const int N=1010,M=5010;
int n,m;
int wf[N];
int h[N],e[M],wt[M],ne[M],idx;
int st[N],cnt[N];
double d[N];
void add(int a,int b,int c)
{wt[idx]=c,e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int spfa(double mid)
{memset(d,0,sizeof d);memset(cnt,0,sizeof cnt);memset(st,0,sizeof st);queue<int>q;for(int i=1;i<=n;i++){q.push(i);st[i]=1;}while(q.size()){int t=q.front();q.pop();st[t]=0;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(d[j]<d[t]+wf[t]-mid*wt[i]){d[j]=d[t]+wf[t]-mid*wt[i];cnt[j]=cnt[t]+1;if(cnt[j]>=n) return 1;if(!st[j])st[j]=1,q.push(j);}}}return 0;
}
int main()
{scanf("%d%d",&n,&m);for(int i=1;i<=n;i++) scanf("%d",&wf[i]);memset(h,-1,sizeof h);for(int i=1;i<=m;i++) {int a,b,c;scanf("%d%d%d",&a,&b,&c);add(a,b,c);}double l=0,r=1e6;while(r-l>1e-4){double mid=(l+r)/2;if(spfa(mid)) l=mid;else r=mid;}printf("%.2lf",r);
}

1165. 单词环（活动 - AcWing）

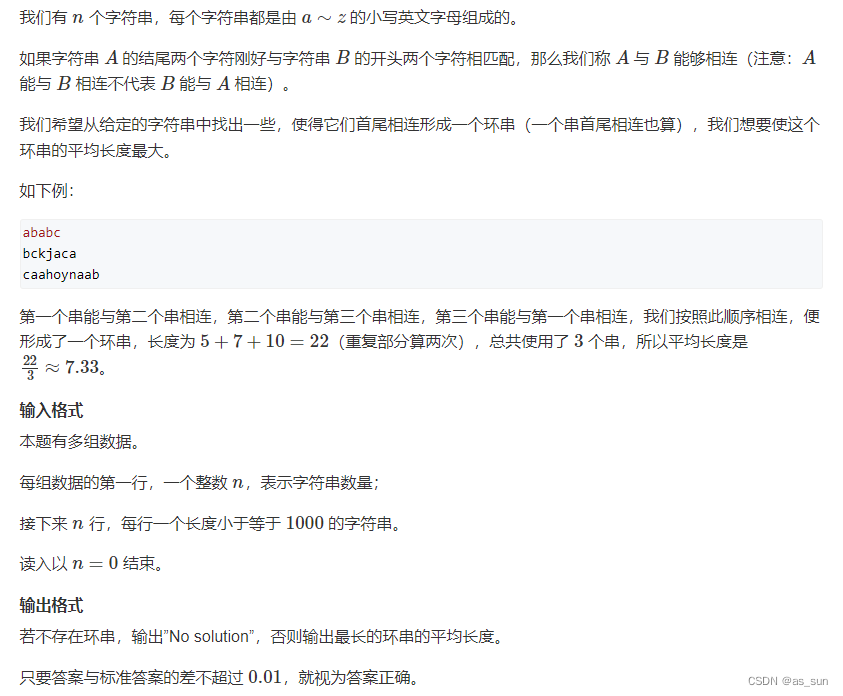
 这道题求环串/单词个数的最大值，显然也是一个01分数问题。那么我们可以套用上一题的思路来写。但是有一点，我们惯性是要在两个单词之间建边的，但是n的范围实在太大，如果在两个单词之间建边，那么根本存不下，所以这题我们另辟蹊径，反正实际有效的只有开头两个字母和结尾两个字母，那么我们直接在开头两个字母和结尾两个字母之间建边，边权等于单词长度。这样将两个单词视为点的话就只有26*26=676个点，建边绰绰有余。然后我们来推公式：

ans=sum(len)/n

ans要不断往大的找，所以mid<=ans:

ans>=mid

sum(len)/n>=mid

sum(len)>=n*mid

sum(len)-n*mid>=0

sum(len-mid)>=0

那么还是和上面一样求正环。

但是本题比较特殊，如果用cnt[j]>=n判退出的话，是会超时的，有一个取巧的经验值，当总的更新次数到4n左右的时候，就可以直接判退出了。其实这个常数可以试出来，如果正常写超时的话，可以用试个常数出来取巧。

#include<bits/stdc++.h>
using namespace std;
const int N=700,M=100010;
int n;
int h[N],w[M],ne[M],e[M],idx;
int cnt[N],st[N];
double d[N];
void add(int a,int b,int c)
{e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
int check(double mid)
{memset(cnt,0,sizeof cnt);memset(st,0,sizeof st);queue<int>q;for(int i=0;i<676;i++) {q.push(i);st[i]=1;}int count=0;while(q.size()){int t=q.front();q.pop();st[t]=0;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(d[j]<d[t]+w[i]-mid){d[j]=d[t]+w[i]-mid;cnt[j]=cnt[t]+1;if(++count>4*N) return 1;if(cnt[j]>=N) return 1;if(!st[j]){st[j]=1;q.push(j);}}}}return 0;
}
int main()
{while(~scanf("%d",&n)){if(!n) break;memset(h,-1,sizeof h);idx=0;for(int i=1;i<=n;i++){string s;cin>>s;int len=s.size();if(len>=2){int a=(s[0]-'a')*26 + s[1]-'a';int b=(s[len-2]-'a')*26+s[len-1]-'a';add(a,b,len);}}if(!check(0)) printf("No solution\n");else{double l=0,r=1000;while(r-l>1e-4){double mid=(l+r)/2;if(check(mid))l=mid;else r=mid;}cout<<l<<endl;}}
}

差分约束

 差分约束可以用来求不等式组的可行解以及满足一系列不等式关系限制的最大值最小值。

为什么呢？因为不等式关系可以与最短路联系起来进而建边构图，比如x1<=x2+c，如果在最短路里面，x1的值更新的条件是什么呢？显然是x1>x2+c，所以如果有x1到x2的最短路，那么就满足上述条件了。所以我们可以建一条x2指向x1的边，边权为c。如果有一系列的不等式关系:x1<=x2+c1,x2<=x3+c2,x3<=x4+c3,...那么如果能确定1的值，求剩下每个点的最大值显然就是求x1到所有点的最短路。由此我们推出一般性的结论。

求不等式组的可行解

源点需要满足的条件：从源点出发，一定可以走到所有的边。（因为边是限制关系，一定要满足所有的限制关系，可以不走到所有的点，因为可能有孤立的点。但是通常可以走到所有的点就一定可以走到所有的边，但是可以走到所有的边未必能走到所有的点）

步骤：

1.先将每个不等式xi<=xj+ck转化成一条从xj走到xi，长度为ck的边

2.找一个超级源点，使得该源点一定可以遍历到所有边

3.从源点求一遍单源最短路

        结果1：如果存在负环，则原不等式组一定无解

        结果2：如果没有负环，则dist[i]就是原不等式组的一个可行解

如何求最大值或者最小值（这里的最值指的是每个变量的最值）

结论：如果是求最小值，则应该求最长路，如果是求最大值，则应该求最短路

问题：如果转化xi<=c（其中c是一个常数）

方法：建立一个超级源点，0，然后建立0到i，长度是c的边即可

ps:求最大值相当于求上界，若有多个上界，显然应该取小的那个，所以是最短路

求最小值是求下界，下界应该是最大的那个，所以是最长路。

方法就是这么个方法，我们来根据例题分析。

1169. 糖果（活动 - AcWing）

思路：差分约束类型的题目，首先就是要把不等式关系理清楚,这里求至少，那么应该求最长路，那么不等关系应该是x1>=x2+c的格式

x=1:a==b =>  a>=b+0,b>=a+0

x=2:a<b => b>=a+1

x=3:a>=b => a>=b+0

x=4:a>b => a>=b+1

x=5:a<=b => b>=a

如此就理出了明着给出的不等关系，但是我们发现没有一个点的值可以直接确定，我们得到的只是相对关系，那么该怎么办呢？这时候就需要找一个超级源点，从它可以遍历所有的边。题目中实际上暗含了一个条件，所有的小朋友都要有糖，那么就是x>=1，因为小朋友的编号是从1开始的，所以我们可以将超级原点定在0处，0到所有点建立一条边权为1的边，既然从0可以到所有的点了，那么也可以到所有的边了。问题自然解决。（实际上最开始将所有点的距离都赋成1，然后将所有点都加入也是可以的。）

这道题其实比较坑的还有一个点，就是需要判负环，但是判负环是会超时的，有一个优化就是将spfa中的队列改成栈。

#include<bits/stdc++.h>
using namespace std;
const int N = 100010, M = 300010;
int n,m;
int h[N],e[M],ne[M],w[M],idx;
long long d[N];
int st[N],cnt[N];
void add(int a,int b,int c)
{w[idx]=c,e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
int spfa()
{stack<int>q;memset(d,-0x3f,sizeof d);d[0]=0;q.push(0);st[0]=1;while(q.size()){int t=q.top();q.pop();st[t]=0;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(d[j]<d[t]+w[i]){d[j]=d[t]+w[i];cnt[j]=cnt[t]+1;if(cnt[j]>=n+1) return 0;if(!st[j]) st[j]=1,q.push(j);}}}return 1;
}
int main()
{scanf("%d%d",&n,&m);memset(h,-1,sizeof h);for(int i=1;i<=m;i++){int x,a,b;scanf("%d%d%d",&x,&a,&b);if(x==1) add(b,a,0),add(a,b,0);else if(x==2) add(a,b,1);else if(x==3) add(b,a,0);else if(x==4) add(b,a,1);else if(x==5) add(a,b,0);}for(int i=1;i<=n;i++) add(0,i,1);if(!spfa()) printf("-1");else {long long res=0;for(int i=1;i<=n;i++) res += d[i];cout<<res;}
}

362. 区间（362. 区间 - AcWing题库）

 思路：首先我们来理一下题意吧，其实第一遍看题目差点没看懂题目的意思。然后又仔细盘了一遍。题目是说，我们要从0到50000中选若干个数，给定一些区间[a,b]，对于每个区间给定一个c，我们选出来的数需要满足至少有c个在区间[a,b]中。

这题乍一看跟差分约束没什么关系，实际上也有一个贪心的做法，但是还是有一个很巧妙的差分约束的思路的。我们从集合的角度来看，定义s[i]表示从1-i中选出了s[i]个数。那么就可以得到如下的不等式关系：

s[i]>=s[i-1]
s[i]-s[i-1]<=1
s[b]-s[a-1]>=c

求至少的话，应该求最长路，不等式应该形如：x1>=x2+c:

s[i]>=s[i-1]+0
s[i-1]>=s[i]-1
s[b]>=s[a-1]+c

不等式关系出来了，那么再找是否有一个超级原点可以到所有的边。

根据第一个不等式i-1到i，依次类推，0可以到所有的点，那么自然可以到所有的边，至此便可以套用差分约束的模板了。

另外由于我们要从0开始，但区间也是从0开始的，所以可以将所有的点往后挪一位。

#include<bits/stdc++.h>
using namespace std;
const int N=50010,M=3*N+10;//3种类型的边
int n;
int h[N],e[M],ne[M],w[M],idx;
int d[N],st[N];
void add(int a,int b,int c)
{e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
void spfa()
{memset(d,-0x3f,sizeof d);d[0]=0;queue<int>q;q.push(0);while(q.size()){int t=q.front();q.pop();st[t]=0;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(d[j]<d[t]+w[i]){d[j]=d[t]+w[i];if(!st[j]) st[j]=1,q.push(j);}}}
}
int main()
{scanf("%d",&n);memset(h,-1,sizeof h);for(int i=1;i<N;i++) {add(i-1,i,0);add(i,i-1,-1);}for(int i=0;i<n;i++){int a,b,c;scanf("%d%d%d",&a,&b,&c);a++,b++;add(a-1,b,c);}spfa();cout<<d[50001];}

ps:由此可以看出差分约束的关键在于不等式和超级源点，这题的处理其实更像dp了。

1170. 排队布局（活动 - AcWing）

思路：这题还是有很多限制条件，所以我们由此推出一些不等式：
d[i-1]<=d[i](1-N排列)
a-b<=l
x-y>=d

要找符合要求的最大值，最大值就应该求最短路，那么不等式应该形如x1<=x2+c:

d[i-1]<=d[i]+0
a<=l+b(b<a)
y<=x-d(x>y)

由第一个条件很容易找到超级源点0，那么就可以套用差分约束的模板。

 不过这里还有一个地方需要注意，1到N的距离可以任意大，这个该如何判断呢。

实际上我们不用真正的把0放入队列，如果不成立，那么就有负环，我们可以跑一边spfa，这时候是将所有点都加入队列；如果没有负环，那么就要考虑从1开始找最短路，d[n]是否为正无穷，如果是正无穷，那么自然该输出-2，否则输出值即可。

#include<bits/stdc++.h>
using namespace std;
const int N=1010,M=30010;
int n,m1,m2;
int h[N],e[M],ne[M],w[M],idx;
int d[N],st[N],cnt[N];
void add(int a,int b,int c)
{e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
bool spfa(int size)
{memset(d,0x3f,sizeof d);memset(st,0,sizeof st);memset(cnt,0,sizeof cnt);queue<int>q;for(int i=1;i<=size;i++){q.push(i);d[i]=0;st[i]=1;}while(q.size()){int t=q.front();q.pop();st[t]=0;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(d[j]>d[t]+w[i]){d[j]=d[t]+w[i];cnt[j]=cnt[t]+1;if(cnt[j]>=n) return 0;if(!st[j]){st[j]=1;q.push(j);}}}}return 1;
}
int main()
{scanf("%d%d%d",&n,&m1,&m2);memset(h,-1,sizeof h);for(int i=1;i<n;i++) add(i+1,i,0);for(int i=1;i<=m1;i++){int a,b,c;scanf("%d%d%d",&a,&b,&c);if(a>b) swap(a,b);//并不能保证大小确定add(a,b,c);}for(int i=1;i<=m2;i++){int a,b,c;scanf("%d%d%d",&a,&b,&c);if(a>b) swap(a,b);add(b,a,-c);}if(!spfa(n)) printf("-1");else{spfa(1);if(d[n]==0x3f3f3f3f) printf("-2");else printf("%d",d[n]);}
}

393. 雇佣收银员（393. 雇佣收银员 - AcWing题库）

思路：这道题的实现同样比较巧妙，我们按照来的开始时间分类，分成24类，然后我们统计每一类种来的人为num[i]，假设挑走x人，那么就可以得到不等式关系了：
x[i-1]<=x[i]
x[i]<=num[i]
x[i-7]+x[i-6]+...+x[i]>=r[i]

这里第二个式子显然不符合差分约束的要求，但是我们可以通过它联系到前缀和，定义s[i]表示从1-i每个开始时间挑选的人的总和。虽然题目说是从0开始，但是我们可以整体后移一位，变成1-24，因为要建立超级源点

那么上式：
s[i-1]<=s[i]
s[i]-s[i-1]<=num[i]
s[i]-s[i-8]>=r[i](i>=8)
s[i]+s[24]-s[16+i]>=r[i](i<=7)

求最少，计算最长路，不等式变成x1>=x2+ck:
s[i]>=s[i-1];
s[i-1]>=s[i]-num[i]
s[i]>=s[i-8]+r[i]
s[i]>=s[16+i]+r[i]-s[24];

注意到最后一个式子实际上还是不符合要求，有s[24]这一项，实际上我们可以枚举s[24],把它变成一个常量，那么问题就解决了。

#include<bits/stdc++.h>
using namespace std;
const int N=30,M=10010;
int h[N],e[M],ne[M],w[M],idx;
int r[N],num[N];
int n;
void add(int a,int b,int c)
{e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
void build(int u)
{memset(h,-1,sizeof h);idx=0;add(0,24,u);add(24,0,-u);for(int i=1;i<=24;i++) {add(i-1,i,0);add(i,i-1,-num[i]);if(i>=8) add(i-8,i,r[i]);else add(16+i,i,r[i]-u);}}
int d[N],st[N],cnt[N];
bool spfa(int u)
{build(u);memset(d,-0x3f,sizeof d);memset(st,0,sizeof st);memset(cnt,0,sizeof cnt);d[0]=0;queue<int>q;q.push(0);while(q.size()){int t=q.front();q.pop();st[t]=0;for(int i=h[t];i!=-1;i=ne[i]){int j=e[i];if(d[j]<d[t]+w[i]){d[j]=d[t]+w[i];cnt[j]=cnt[t]+1;if(cnt[j]>=25) return 0;if(!st[j]){st[j]=1;q.push(j);}}}}return 1;
}
int main()
{int t;scanf("%d",&t);while(t--){for(int i=1;i<=24;i++) scanf("%d",&r[i]);scanf("%d",&n);memset(num,0,sizeof num);for(int i=1;i<=n;i++){int c;scanf("%d",&c);c++;num[c]++;}int flag=0;for(int i=0;i<=1000;i++){if(spfa(i)){flag=1;break;}}if(flag) printf("%d\n",d[24]);else printf("No Solution\n");}
}