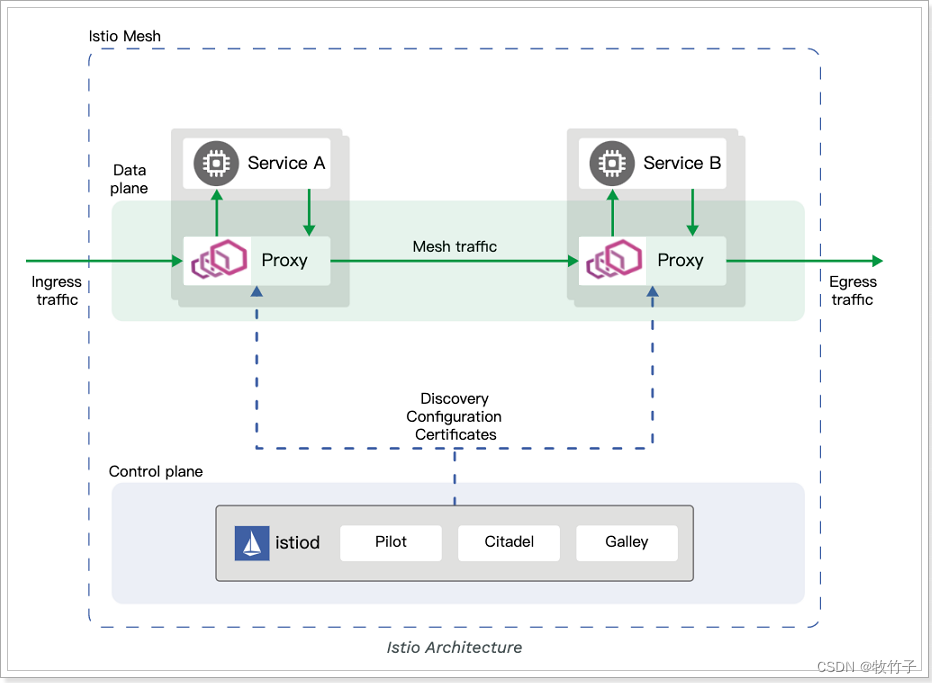
什么是红黑树
红黑树(Red Black Tree)是一种自平衡二叉查找树。它是在 1972 年由 Rudolf Bayer 发明的,当时被称为平衡二叉 B 树(symmetric binary B-trees)。后来,在 1978 年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”。
由于其自平衡的特性,保证了最坏情形下在 O(logn) 时间复杂度内完成查找、增加、删除等操作,性能表现稳定。
在 JDK 中,TreeMap、TreeSet 以及 JDK1.8 的 HashMap 底层都用到了红黑树。
为什么需要红黑树
红黑树的诞生就是为了解决二叉查找树的缺陷。
二叉查找树是一种基于比较的数据结构,它的每个节点都有一个键值,而且左子节点的键值小于父节点的键值,右子节点的键值大于父节点的键值。这样的结构可以方便地进行查找、插入和删除操作,因为只需要比较节点的键值就可以确定目标节点的位置。但是,二叉查找树有一个很大的问题,就是它的形状取决于节点插入的顺序。如果节点是按照升序或降序的方式插入的,那么二叉查找树就会退化成一个线性结构,也就是一个链表。这样的情况下,二叉查找树的性能就会大大降低,时间复杂度就会从 O(logn) 变为 O(n)。
红黑树的诞生就是为了解决二叉查找树的缺陷,因为二叉查找树在某些情况下会退化成一个线性结构。
红黑树的特点
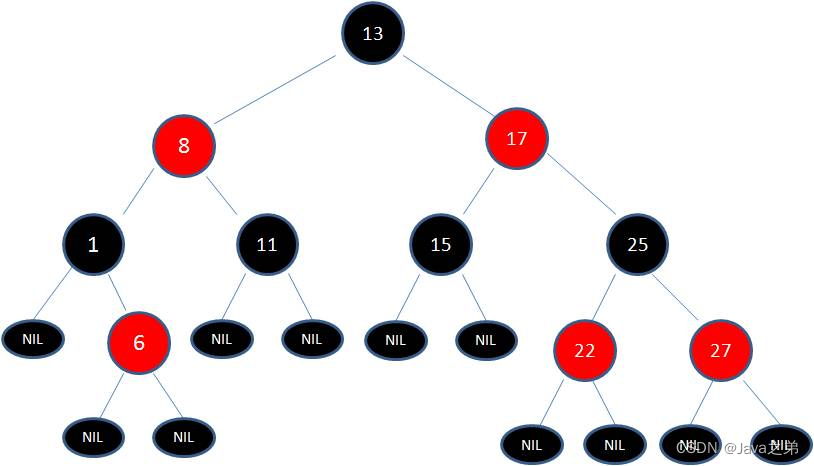
- 每个节点非红即黑。黑色决定平衡,红色不决定平衡。这对应了 2-3 树中一个节点内可以存放 1~2 个节点。
- 根节点总是黑色的。
- 每个叶子节点都是黑色的空节点(NIL 节点)。这里指的是红黑树都会有一个空的叶子节点,是红黑树自己的规则。
- 如果节点是红色的,则它的子节点必须是黑色的(反之不一定)。通常这条规则也叫不会有连续的红色节点。一个节点最多临时会有 3 个节点,中间是黑色节点,左右是红色节点。
- 从根节点到叶节点或空子节点的每条路径,必须包含相同数目的黑色节点(即相同的黑色高度)。每一层都只是有一个节点贡献了树高决定平衡性,也就是对应红黑树中的黑色节点。
正是这些特点才保证了红黑树的平衡,让红黑树的高度不会超过 2log(n+1)。
红黑树代码实现
c++版本
#include <iostream>
#include <queue>enum Color {RED,BLACK
};template <typename T>
struct Node {T data;Color color;Node* parent;Node* left;Node* right;
};template <typename T>
class RedBlackTree {
public:RedBlackTree() : root(nullptr) {}void insert(T data) {Node<T>* newNode = new Node<T>();newNode->data = data;newNode->color = RED;newNode->left = nullptr;newNode->right = nullptr;if (root == nullptr) {root = newNode;root->color = BLACK;} else {Node<T>* current = root;Node<T>* parent = nullptr;while (current != nullptr) {parent = current;if (data < current->data) {current = current->left;} else {current = current->right;}}newNode->parent = parent;if (data < parent->data) {parent->left = newNode;} else {parent->right = newNode;}insertFixup(newNode);}}void printLevelOrder() {if (root == nullptr) {return;}std::queue<Node<T>*> q;q.push(root);while (!q.empty()) {Node<T>* current = q.front();q.pop();std::cout << current->data << " ";if (current->left != nullptr) {q.push(current->left);}if (current->right != nullptr) {q.push(current->right);}}}private:Node<T>* root;void insertFixup(Node<T>* node) {while (node->parent != nullptr && node->parent->color == RED) {if (node->parent == node->parent->parent->left) {Node<T>* uncle = node->parent->parent->right;if (uncle != nullptr && uncle->color == RED) {node->parent->color = BLACK;uncle->color = BLACK;node->parent->parent->color = RED;node = node->parent->parent;} else {if (node == node->parent->right) {node = node->parent;rotateLeft(node);