单调栈总结以及Leetcode案例解读与复盘

一、单调栈是什么？

单调栈（monotonous stack）是指栈的内部从栈底到栈顶满足单调性的栈结构。

二、如何维护单调性

新元素入栈时，会与栈顶元素进行比较，使得栈始终保持单调性。

for example，如果需要构造一个从栈底到栈顶单调递减的栈

如果要插入的元素x是小于栈顶元素的，直接插入即可。
如果要插入的元素x是大于栈顶元素的，说明需要弹出部分元素直到x是小于栈顶元素的，以确保插入该元素x后栈的单调性

while(stack1.length && nums[i] > stack1.at(-1)){// operations #1stack1.pop();
}// operations #2**
stack1.push(nums[i]);

上面的代码里有两处可以增加附加操作（即operations #1和operations #2）

三、维护单调性过程中元素与栈顶元素之间的关系

下面以创建一个单调递减栈为例讲解一下。

被遍历到的元素入栈时：

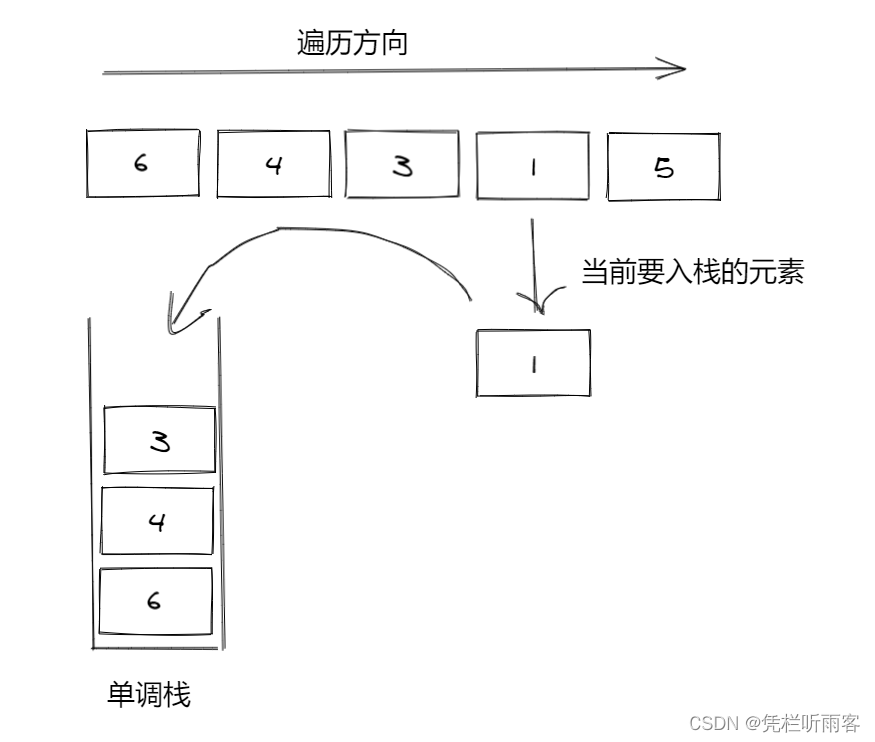
如上图所示，

添加元素1入栈时，由于元素1能直接入栈且不破坏单调性，因此可以直接push进入。

在1入栈前，我们可以观察到，栈中最小的元素即为栈顶的3，因此即将入栈的1在原数组位置的左侧比自己大的元素只能是 3。

⇒ 如果一个元素入栈后不破坏单调栈的单调性，那么栈顶元素就是待入栈元素在原数组位置左侧第一个比自己大的元素。

⇒ 如果要求一个元素左边第一个比自己大的元素，就从左向右遍历，构建单调递减栈。更新待入栈的元素的左侧第一个比自己大的元素是栈顶元素。

⇒ 如果要求一个元素左边第一个比自己小的元素，就从左向右遍历，构建单调递增栈。更新待入栈的元素的左侧第一个比自己小的元素是栈顶元素。
当栈内元素出栈时：

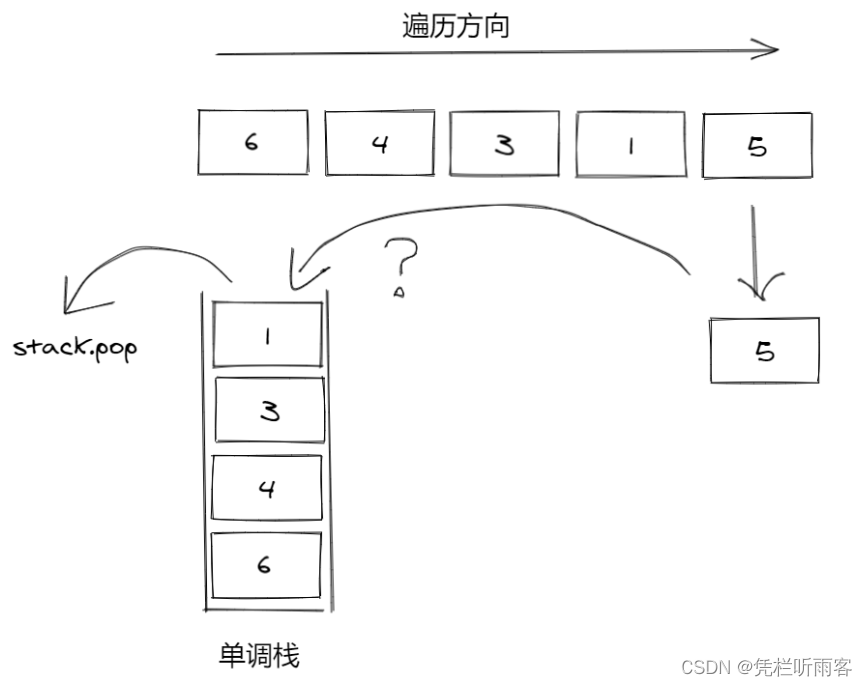
在这里插入图片描述

如上图，

当元素5要入栈时，发现入栈后不能满足单调性。栈顶的1比5小，因此必须pop出栈顶元素1。

这里即将被pop出的1和待入栈的5也蕴含一种关系：5是打破1所在位置单调性的原因，假如5和1之间还有个元素0.2，那么0.2 会被压入栈，并不会打破栈的单调性，因此待入栈的5是即将出栈的1右侧第一个比自己大的元素。

⇒ 由于一个待入栈元素要入栈，导致一个元素出栈时，这个待入栈元素是该出栈元素右侧第一个比自己大的元素。

⇒ 要求一个元素右边第一个比自己大的数，就从左向右遍历，构造单调递减栈，更新出栈元素的右侧最大值为待入栈元素。

⇒ 要求一个元素右边第一个比自己小的数，就从左向右遍历，构造单调递增栈，更新出栈元素的右侧最大值为待入栈元素。

总结，从左向右，待入栈的元素只能找出左侧的符合某个特性的元素，右侧信息是不知道的；待出栈的元素只能知道右侧的符合某个特性的元素。

四、基础案例

问题：给定一个数组，找到每个元素的下一个更大元素。如果不存在更大的元素，则将其设为-1。

示例：

输入：[2, 5, 9, 3, 1, 12, 6, 8, 7]

输出：[5, 9, 12, 12, 12, -1, 8, -1, -1]

解释：对于输入数组中的每个元素，找到它右边第一个比它大的元素。如果不存在这样的元素，则将其设为-1。因此，对于2，右边第一个比它大的元素是5；对于5，右边第一个比它大的元素是9；对于9，右边第一个比它大的元素是12；对于3、1、6，它们右边都存在比它们大的元素，所以对应的结果分别是12、12、12；对于12、8、7，它们右边都不存在比它们大的元素，所以对应的结果分别是-1、-1、-1。

从左向右遍历构造单调递减栈，更新出栈元素的右侧最大值为待入栈元素

/*** @param {number[]} temperatures* @return {number[]}*/
var nextGreaterElements= function (nums) {let stack = [];let res = new Array(nums.length).fill(-1);for(let i = 0; i < nums.length ; i++){while(stack.length && nums[i] > nums[stack.at(-1)]){res[stack.at(-1)] = nums[i];stack.pop()}stack.push(i);}return res;
};// 示例用法
const nums = [2, 5, 9, 3, 1, 12, 6, 8, 7];
const result = nextGreaterElements(nums);
console.log(result); // 输出: [5, 9, 12, 12, 12, -1, 8, -1, -1]

739 每日温度

https://leetcode.cn/problems/daily-temperatures/solutions/868874/yi-pian-ti-jie-gao-ding-dan-diao-zhan-we-2pkf/

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

从左向右遍历构造单调递减栈，更新出栈元素的右侧最大值为待入栈元素

/*** @param {number[]} temperatures* @return {number[]}*/
var dailyTemperatures = function (temperatures) {let stack = [];let res = new Array(temperatures.length).fill(0);for(let i = 0; i < temperatures.length ; i++){while(stack.length && temperatures[i] > temperatures[stack.at(-1)]){res[stack.at(-1)] = i - stack.pop();}stack.push(i);}return res;
};

496. 下一个更大元素

nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置右侧的 第一个 比 x ****大的元素。

给你两个 没有重复元素 的数组 nums1 和 nums2 ，下标从 0 开始计数，其中nums1 是 nums2 的子集。

对于每个 0 <= i < nums1.length ，找出满足 nums1[i] == nums2[j] 的下标 j ，并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素，那么本次查询的答案是 -1 。

返回一个长度为 nums1.length 的数组 ans 作为答案，满足 ans[i] 是如上所述的 下一个更大元素 。

思路：

只需要计算nums2中每个元素的下一个，然后nums1根据map可以去获取，可以这么做的理由是因为nums1 的元素在nums2 里都可以找到。而且nums2 的元素是没有重复的。

⇒ 找出下一个更大的元素。
从左向右遍历构造单调递减栈，更新出栈元素的右侧最大值为待入栈元素

  var nextGreaterElement = function(nums1, nums2) {let res = new Array(nums1.length).fill(-1);let map2 = new Map();let stack = []for(let i = 0; i < nums2.length; i++){map2.set(nums2[i],-1)while(stack.length && nums2[i] > stack.at(-1)){map2.set(stack.pop(), nums2[i]);}stack.push(nums2[i]);}console.log(map2)for(let i = 0; i < nums1.length; i++){res[i] = map2.get(nums1[i]);}return res;
};

503. 下一个更大元素

如果提到循环、首尾相连等字样，应该能立马联想到模运算（求余运算），也就是下标 % 长度，本题中就用到了模运算。

给定一个循环数组 nums （ nums[nums.length - 1] 的下一个元素是 nums[0] ），返回 nums 中每个元素的 下一个更大元素 。

数字 x 的 下一个更大的元素 是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1 。

思路：

其实最简单的方式就是将数组进行翻倍处理，这里的翻倍不是扩容为两倍，而是遍历两遍就可以了，采用模运算的方式来处理，不是真正地翻倍

⇒ 找出下一个更大的元素。
从左向右遍历构造单调递减栈，更新出栈元素的右侧最大值为待入栈元素

对 [1,2,4,3]

遍历 2 遍的做法 0 1 2 3 4%4 5%4 6%4 7%4

⇒ nums.length * 2 - 1

var nextGreaterElements = function(nums) {let stack = [];let res = new Array(nums.length).fill(-1);for(let i = 0;i<2*nums.length; i++){while(stack.length && nums[i%nums.length] > nums[stack.at(-1)]){res[stack.at(-1)] = nums[i%nums.length];stack.pop();}stack.push(i%nums.length);}return res;
};

402. 移掉 K 位数字

给你一个以字符串表示的非负整数 num 和一个整数 k ，移除这个数中的 k **位数字，使得剩下的数字最小。请你以字符串形式返回这个最小的数字。

示例 1 ：

输入：num = "1432219", k = 3
输出："1219"
解释：移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219 。

如果有 m+1 位数字，S1

$a_0a_1a_2....a_m$

需要去掉n位数字，S2

$a_i,a_k,,,,a_n$

剩余的 m+1-n 位。S3

假如用去掉的 n 位数字中的一个数字

$a_i （a_i < a_j）$

替换剩余的 S3 里面的最大的字符 (a_j)，那么新的数字会比原来的S3 要小，因此，我们用来去掉的n位数字中的每一个数字都需要大于剩余的数字

⇒ 去掉前N个最大的数字。

⇒ 通过单调栈去掉极大值，尖峰。

注意点：

遍历完毕后，k个数字没有移除完，比如数字123456789，移除3个数字，按照上面的分析，得出的结果还是123456789，出现这种情况是因为移除部分数字后，得出的结果是一个高位递增的数，所以无法再移除了，这个时候，只要出现这种情况，将低位的数字移除掉剩余个数即可，可以仔细想想这一个特殊点

通过上述的解释，我们需要从左向右遍历数组，然后构建单调递增栈，尽量将小的数往高位放。

var removeKdigits = function(num, k) {if(k === num.length){return "0";}let stack = [];for(let i = 0; i < num.length; i++){// 遇到更小的数,将大的数弹出，维护k的大小。while(k && stack.length && num[i]< stack.at(-1)  ){stack.pop();k--;}// 维护的是一个递增的栈，但是首位不能是0if(!(nums[i]==="0" && stack.length === 0)){stack.push(num[i]);}}// 把低位的删除即可 ||单调递增while(k>0 && stack.length){stack.pop();k--;}return stack.length === 0 ? "0" : stack.join("");};

581. 最短无序连续子数组

给你一个整数数组 nums ，你需要找出一个 连续子数组 ，如果对这个子数组进行升序排序，那么整个数组都会变为升序排序。

请你找出符合题意的最短子数组，并输出它的长度。

示例 1：

输入：nums = [2,6,4,8,10,9,15]
输出：5
解释：你只需要对 [6, 4, 8, 10, 9] 进行升序排序，那么整个表都会变为升序排序。

示例 2：

输入：nums = [1,2,3,4]
输出：0

示例 3：

输入：nums = [1]
输出：0

思路一

将nums 进行排序获得新的数组sortedArr
两个数组进行从左到右进行对比，找出第一位不同的元素，用 left 标志位置，再从右到左，找不同的元素，用right标志。
right - left + 1 就是子数组的长度。

思路二

从左向右，构造一个单调递增的栈，一旦遇到需要出栈的，说明要入栈的元素小于栈顶元素。
从右向左，构造一个单调递减的栈，一旦遇到需要出栈的，说明要入栈的元素大于栈顶元素


/*** @param {number[]} nums* @return {number}*/
var findUnsortedSubarray = function(nums) {if(nums.length === 1){return 0;}// 从左到右构造一个单调递增的栈let left = nums.length - 1;let stack1 = [];for(let i = 0; i < nums.length; i++){while(stack1.length && nums[i] < nums[stack1.at(-1)]){left = Math.min(left, stack1.pop());}stack1.push(i);}// 从右到左构造一个单调递减的栈let right = 0;let stack2 = [];for(let i = nums.length - 1; i >= 0; i--){while(stack2.length && nums[i] > nums[stack2.at(-1)]){right = Math.max(right, stack2.pop());}stack2.push(i);}return left > right ? 0 : right - left + 1;
};

例题1

对山峰群编号1-N，观测员站在奇数编号山顶观测其左边比当前山峰高的个数，观测员站在奇数编号山顶观测其右边比当前山峰高的个数。
统计观测员观测到的山峰个数和。注：相同高度的山峰能被遮挡，只能看到最近的一座山峰。

1 <= N <= 100000
1 <= height <= 1000000

举例1
N = 6 height[6] = {16, 5, 3, 10, 21, 7} 观测到的山峰个数为8 = 0 + 3 + 2 + 1 + 2 + 0

思路：

从左到右遍历构建一个单调递减栈，一旦遇到更大的，需要将栈里小于更大元素都清掉，因为右边元素能看到的左边的山已经被更大的元素盖住了。
从右到左也构建一个单调递减栈。

const NumberOfMountainSeen = ( height) =>{let oddStack = []let oddResult = []for(let i = 0; i < height.length; i++){oddResult.push(oddStack.length ? oddStack.length : 0)while(oddStack.length && height[i] >= oddStack.at(-1)){oddStack.pop()}oddStack.push(height[i])}let evenStack = []let evenResult = []for(let i = height.length - 1; i >= 0; i--){evenResult.unshift(evenStack.length ? evenStack.length : 0)while(oddStack.length && height[i] >= evenStack.at(-1)){evenStack.pop()}evenStack.push(height[i])}let sum = 0;for(let i = 0; i < height.length; i++){if(i%2==0){sum+=oddResult[i]}else{sum+=evenResult[i]}}console.log(evenResult)return sum;}
console.log(NumberOfMountainSeen([16,5,3,10,21,7]))