约数问题：

试除法：

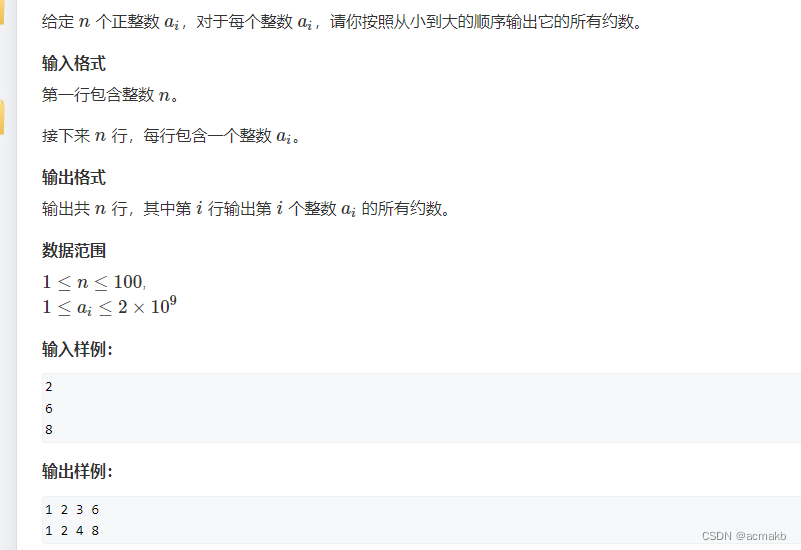
d|n 那么 n/d|n 也是成立的-----> 成对出现的
d<=n/d  ===d小于等于根号n 

举例：

假如2是12的约数，那么6也是12的约数。

#include <iostream>
#include <algorithm>
#include <vector>
#include<cstdio> 
using namespace std;vector<int> get_divisors(int x)
{vector<int> res;//因为约数成对出现，所以只需要循环到根号xfor (int i = 1; i <= x / i; i ++ )//约数可以从1开始枚举，只要可以整除就行if (x % i == 0)// 是一个约数 {res.push_back(i);//处理极端情况 比如 16 = 4 * 4if (i != x / i) res.push_back(x / i);// 防止两个约数一样 只能放一个  }sort(res.begin(), res.end());return res;
}int main()
{int n;cin >> n;while (n -- ){int x;cin >> x;auto res = get_divisors(x);for (auto x : res) cout << x << ' ';cout << endl;}return 0;
}

约数个数

870. 约数个数 - AcWing题库

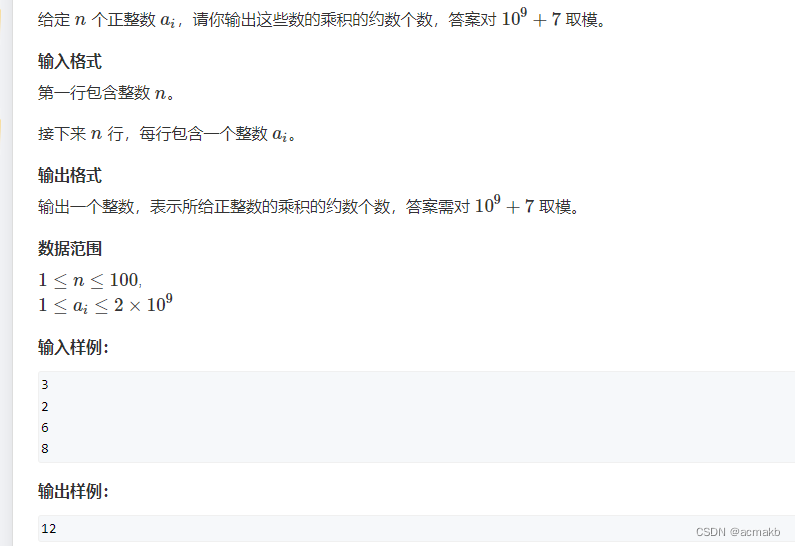
基础知识铺垫：

一般地，对自然数n进行分解质因数，设n可以分解为n=p⑴^α⑴·p⑵α*⑵·…·p(k)^α（k）

其中p⑴、p⑵、…p（k）是不同的质数，α⑴、α⑵、…α（k）是正整数，则形如

n=p⑴^β⑴·p⑵β*⑵·…·p(k)^β（k）的数都是n的约数，其中β⑴可取a⑴+1个值：0,1,2，…，α⑴；β⑵可取α⑵+1个值：0,1,2，…，α⑵…；β（k）可取a(k)+1个值：0,1,2，…，α（k）.且n的约数也都是上述形式，根据乘法原理，n的约数共有

（α⑴+1）（α⑵+1）…（α（k）+1） ⑺个。

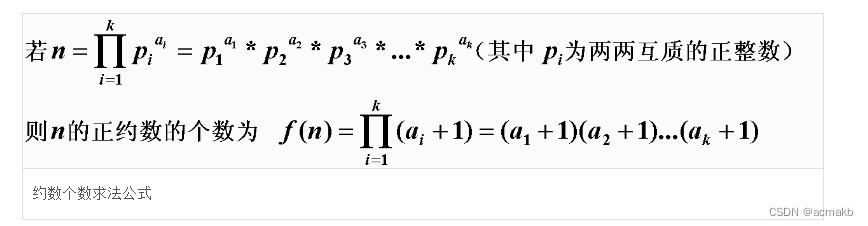
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 110, mod = 1e9 + 7;
int main(){int n;cin >> n;unordered_map<int, int> primes;while (n -- ){int x;cin >> x;for (int i = 2; i <= x / i; i ++ )//质数那一部分 while (x % i == 0)// 可以除开 {x /= i;primes[i] ++ ;//   primes[i] 存放的是以i为底数的幂是多少，就是可以除多少次}if (x > 1) primes[x] ++ ;// x 最多存在一个比较大的质因数 }LL res=1; // 因为存放的pair类型 p.first获取第一关键字 p.second获取第二关键字for (auto p : primes) res = res * (p.second + 1) % mod;cout << res << endl;return 0;
} 

约数之和：

871. 约数之和 - AcWing题库

那么n的(a₁+1)(a₂+1)(a₃+1)…(ak+1)个正约数的和为
f(n)=(p10+p11+p12+…p1a1)(p20+p21+p22+…p2a2)…(pk0+pk1+pk2+…pkak）

如果 N = p1^c1 * p2^c2 * ... *pk^ck
约数个数： (c1 + 1) * (c2 + 1) * ... * (ck + 1)
约数之和： (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)

问题转化为如何求：(p1^0 + p1^1 + ... + p1^c1)，这一步就是获取每一位数字的逆运算。

思路：c1次幂对应c1+1项，所有应该提前将一项准备处理。即t = (t * a + 1)

 		LL a = p.first, b = p.second;//b为幂LL t = 1;//局部初始化while (b -- ) t = (t * a + 1) % mod;res = res * t % mod;

#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <vector>
using namespace std;
typedef long long LL;
const int N = 110, mod = 1e9 + 7;
int main()
{int n;cin >> n;unordered_map<int, int> primes; // 第一个的是底数 第二个的是幂 while (n -- ){int x;cin >> x;for (int i = 2; i <= x / i; i ++ )while (x % i == 0){x /= i;primes[i] ++ ;}if (x > 1) primes[x] ++ ;}LL res = 1;for (auto p : primes){LL a = p.first, b = p.second;LL t = 1;while (b -- ) t = (t * a + 1) % mod;res = res * t % mod;}cout << res << endl;return 0;
}