一、题目
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
- 例如,从根节点到叶节点的路径
1 -> 2 -> 3表示数字123。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
示例 1:
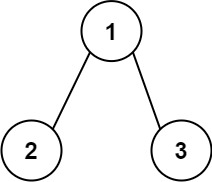
输入:root = [1,2,3] 输出:25 解释: 从根到叶子节点路径 1->2代表数字 12从根到叶子节点路径 1->3代表数字 13因此,数字总和 = 12 + 13 = 25
示例 2:
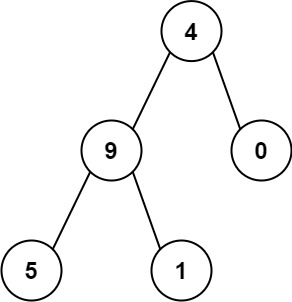
输入:root = [4,9,0,5,1] 输出:1026 解释: 从根到叶子节点路径 4->9->5代表数字 495从根到叶子节点路径 4->9->1代表数字 491从根到叶子节点路径 4->0代表数字 40因此,数字总和 = 495 + 491 + 40 = 1026
提示:
- 树中节点的数目在范围
[1, 1000]内 0 <= Node.val <= 9- 树的深度不超过
10
二、思路解析
树形结构,我们也应该有往递归上靠的意识,因为这个结构本身就是由一个个相同的子问题构成的。
而每层递归都要处理的问题,就是把父节点的值 * 10 之后加上根节点的值。同时只要还有左子树和右子树,就继续递归下去。
代码部分不难看懂的,具体实现也不复杂,具体请看下面代码👇
三、完整代码
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int sumNumbers(TreeNode root) {return dfs(root , 0);}public int dfs(TreeNode root , int preSum){preSum = preSum * 10 + root.val;if(root.left == null && root.right == null){return preSum;}int ret = 0;if(root.left != null){ret += dfs(root.left , preSum);}if(root.right != null){ret += dfs(root.right , preSum);} return ret;}
}以上就是本篇博客的全部内容啦,如有不足之处,还请各位指出,期待能和各位一起进步!














![[力扣 Hot100]Day33 排序链表](https://img-blog.csdnimg.cn/direct/7b58508b39b248b98d490404718911b5.png)