【数据结构】图—

【数据结构】图——最短路径

最短路径问题：从在带权有向图G中的某一顶点出发，找出一条通往另一顶点的最短路径，最短也就是沿路径各边的权值总和达到最小。

最短路径分为图中单源路径和多源路径。

本文会介绍Dijkstra和Bellman-Ford解决单源路径的问题

Floyd-Warshall解决多路径的问题

单源最短路径--Dijkstra算法

单源问题，对于图中给定的结点u，求出到达各个结点v的路径代价和最小。最小路径可能是直接u->v

也可能是从u->t->v 。

Dijkstra算法就是解决所有边非负权值的最短路径。一般是从给出点u到终点v.

算法的思路

将图中的所有结点可以分为S和Q，S是已经确定最短路径的集合，Q是还没被访问的集合)(初始化时，将s放到集合中)

每一次从Q中选出一个s到Q代价最小的点u，把u从s移出放到S中，对u的相邻v 进行松弛更新。

松弛更新：判断s->u(已经确定了) u->v的路径是否小于s->v（已经确定的）

如果是的话，就更新s->v

直到更新所有的Q结点

在我们的模拟实现中

保存一张dist[]数组，用来表示s到某点的最短路径

S[]数组用来表示已经确定最短路径的顶点、

pPath用来存储路径前一个顶点的下标

通过画图梳理这个过程

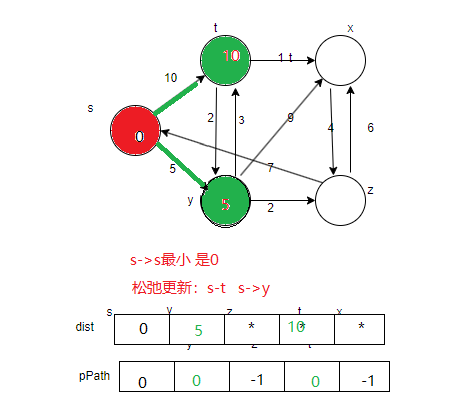
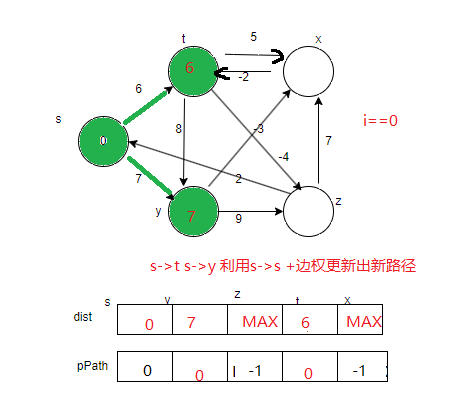
首次初始化时，dist数组s位置是0，其它为无穷，pPath数组s位置是缺省值

第二轮：寻找最短路径s-s 松弛更新出s->t s->y

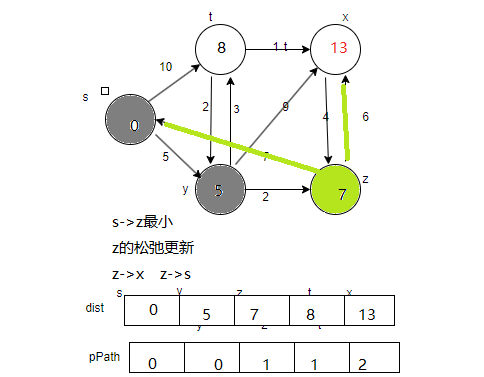
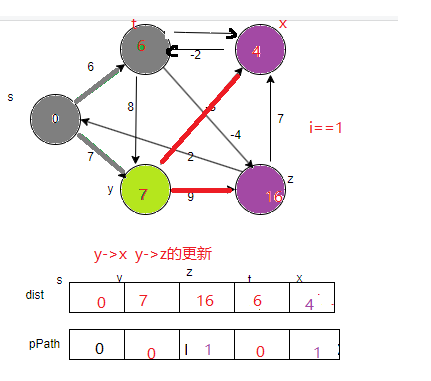
第三步选出最小v s->y(s->s已经被标记过)

松弛更新出s-y-t s-y-x s-y-z

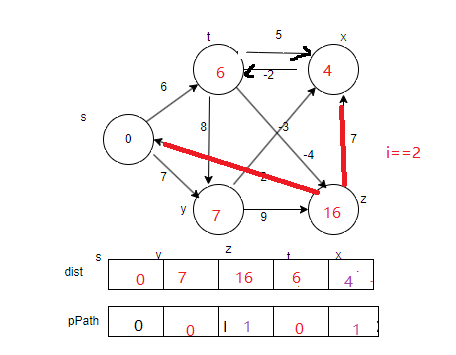
第三轮选边选出s->z 对z相邻的边松弛更新

s->z->x(13)

s->z->s（14 不更新）

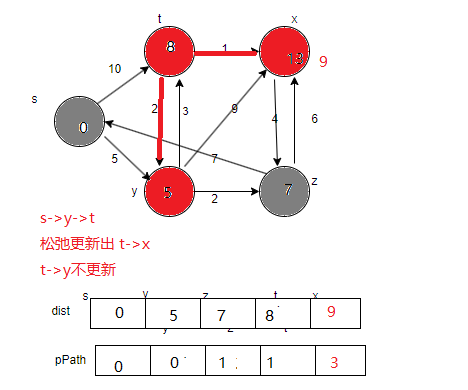
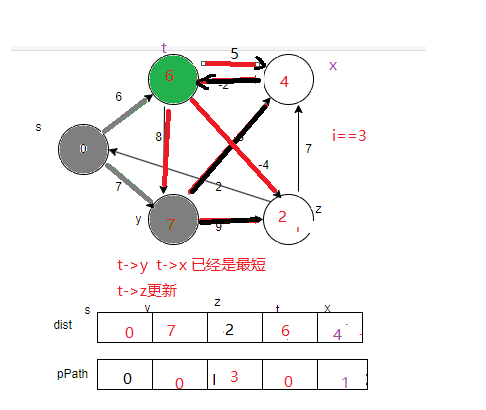
第四轮

选边s->t

第五轮选出s->x 松弛更新出 x->z(不更新，已经是最短路径)

松弛更新不适合用于带负权值的路径

因为无法确定第一轮的最小值

		void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath){size_t srci = GetVertexIndex(src);size_t n = _vertexs.size();dist.resize(n, MAX_W);pPath.resize(n, -1);//自身就是0dist[srci] = W();pPath[srci] = srci;//标记容器vector<bool> S(n, false);for (size_t j = 0; j < n; j++){int u = 0;W min = MAX_W;for (size_t i = 0; i < n; i++){if (S[i] == false && dist[i] < min){u = i;min = dist[i];}}S[u] = true;//松弛更新for (size_t v = 0; v < n; v++){if (S[v] == false && _matrix[u][v] != MAX_W &&dist[u] + _matrix[u][v] < dist[v]){dist[v] = dist[u] + _matrix[u][v];pPath[v] = u;}}}}

单源最短路径--Bellman-Ford算法

迪杰斯特拉算法不能解决带负权值边的最短路径，贝尔曼福特就采用暴力的方式解决了带负权值边的路径问题，还能判断出回路是否带有负权值。

贝尔曼福特算法的思路是将 srci-> j的路径问题划分为srci-> i i->j的路径最短问题

对于从源顶点 s 到目标顶点 j 的路径来说，如果存在从源顶点 s 到顶点 i 的路径，还存在一条从顶点 i 到顶点 j 的边，并且其权值之和小于当前从源顶点 s 到目标顶点 j 的路径长度，则可以对顶点 j j 的估计值和前驱顶点进行松弛更新。

是利用已经确定的最短路径srci -i 再加上i->j的边权来更新的最短路径。

确定完所有的顶点后，都必须重新进行更新，因为每一条路径的确定，都有可能影响前一轮的路径更新。故需要遍历K次。K为N次。(因为所有的点都在变，都需要更新。)

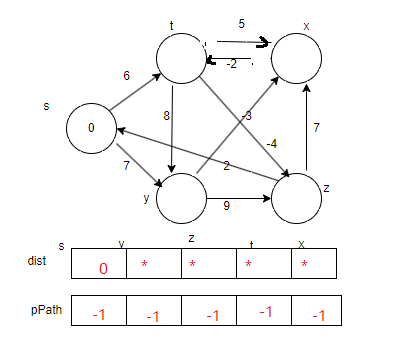
初始化时，dist[srci]初始化为缺省值

第一次i==0时，更新出t y

第二次,i==1更新出x z

i==2时，更新出 x s(不更新，目前是最短路径)

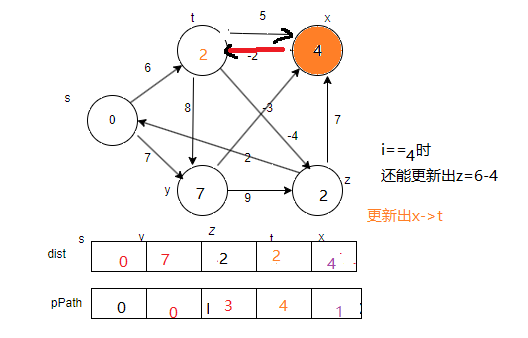
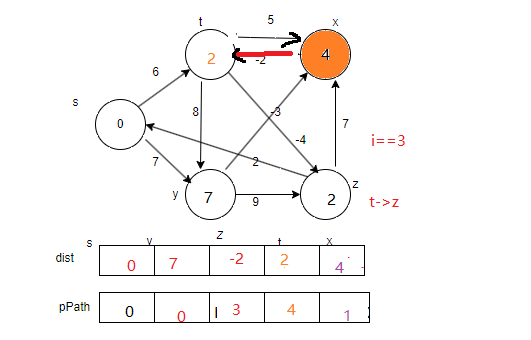
i==3时，更新出t->z

i==4时，用x更新出t

结束第一轮

此时还需要进行下一轮的更新

下一轮再i==3时，更新出t->z=-4

		bool BellmanFord(const V& src, vector<W>& dist, vector<int>& pPath){size_t n = _vertexs.size();size_t srci = GetVertexIndex(src);dist.resize(n, MAX_W);pPath.resize(n, -1);dist[srci] = W();//最多更新k轮for (size_t k = 0; k < n; k++){bool updata = false;cout << "更新第:" << k << "轮" << endl;//srci->i+i->jfor (size_t i = 0; i < n; i++){for (size_t j = 0; j < n; j++){if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j]){updata = true;cout << _vertexs[i] << "->" << _vertexs[j] << ":" << _matrix[i][j] << endl;dist[j] = dist[i] + _matrix[i][j];pPath[j] = i;}}}if (!updata)break;}//如果还能更新，就是带负路径for (size_t i = 0; i < n; i++){for (size_t j = 0; j < n; j++){if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j]){return false;}}}return true;}

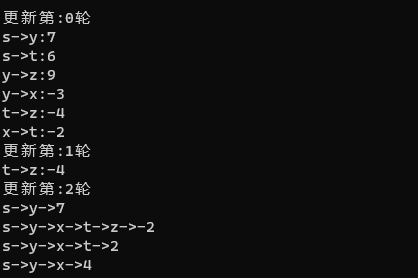
利用程序编写过程和我们的画图一致

贝尔曼福特算法是暴力求解，有相当高的时间复杂度O(N^3)，但是能够解决负权值问题。

多源最短路径--Floyd-Warshall算法

Floyd-Warshall算法是解决任意两点间的最短路径的一种算法。

弗洛伊德算法考虑的是中间最短路径的中间结点，设k是p的一个中间节点，那么从i到j的最短路径p就被分成i到k和k到j的两段最短路径p1，p2。p1是从i到k且中间节点属于{1，2，…，k-1}取得的一条最短路径。p2是从k到j且中间节点属于{1，2，…，k-1}取得的一条最短路径。

Floyd-Warshall算法是一种动态规划算法，其运行时间为o(n^3)与最短路径路径上通常的假设一样，假设权重可以为负，但不能有权重为负的环路。

如果存在从顶点 i 到顶点 k 的路径，还存在从顶点 k 到顶点 j 的路径，并且这两条路径的权值之和小于当前从顶点 i 到顶点 j 的路径长度，则可以对顶点 j 的估计值和前驱顶点进行松弛更新。

算法原理：

费洛伊徳算法就是将最短路径分成dist[i][k]+ dist[k][j]与dist[k][j]的问题

算法需要一个二维的vvdist记录最短路径，vvpPath标记父路径

将直接相连的视作最短路径

进行k次更新（K为n，i和j都在变换）

动态规划更新vvdist

注意vvpPath[i][j]的前一个不再是i而应该是递归的vvpPath[k][j]，可能变化一次，也可能变化好多次

		void FloydWarshall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath){size_t n = _vertexs.size();vvDist.resize(n, vector<W>(n, MAX_W));vvpPath.resize(n, vector<int>(n, -1));//更新权值和父路径for (size_t i = 0; i < n; i++){for (size_t j = 0; j < n; j++){if (_matrix[i][j] != MAX_W){vvDist[i][j] = _matrix[i][j];vvpPath[i][j] = i;}if (i == j){vvDist[i][j] = W();}}}//O(N^3)//最多更新k次for (size_t k = 0; k < n; k++){for (size_t i = 0; i < n; i++){for (size_t j = 0; j < n; j++){//存在 i->k  k->j 且<dist[i][j]if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W&& vvDist[i][k] + vvDist[k][j] < vvDist[i][j]){vvDist[i][j] = vvDist[i][k] + vvDist[k][j];vvpPath[i][j] = vvpPath[k][j];}}}// 打印权值和路径矩阵观察数据for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){if (vvDist[i][j] == MAX_W){//cout << "*" << " ";printf("%3c", '*');}else{//cout << vvDist[i][j] << " ";printf("%3d", vvDist[i][j]);}}cout << endl;}cout << endl;for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){//cout << vvParentPath[i][j] << " ";printf("%3d", vvpPath[i][j]);}cout << endl;}cout << "=================================" << endl;}}